Ромботриаконтаедр

Ромботриаконтаедр
Тип	каталанове тіло
Граней	30
Ребер	60
Вершин	32
Конфігурація вершин	V3.5.3.5
Діаграма Коксетера
Група симетрії	Ih, H3, [5,3], (*532)
Площа поверхні	$S=12{\sqrt {5}}\,a^{2}$
Об'єм	$V=4{\sqrt {5+2{\sqrt {5}}}}\,a^{3}$
Двогранний кут (градуси)	144°
Дуальний многогранник	ікосододекаедр
ізоедричний, ізотоксальний, зоноедр
Розгортка

Тривимірна модель ромботриаконтаедра

У геометрії ромботриаконтаедр або ромбічний триаконтаедр, який іноді називають просто триаконтаедром (від грец. τριάκοντα (грец. τριάντα) — «тридцять» і εδρον — «грань»), оскільки це найпоширеніший тридцятигранний многогранник — опуклий многогранник із 30 ромбічними гранями. Має 60 ребер і 32 вершини двох типів: 12 розташовані при гострих кутах 5 ромбів, решта 20 — при тупих кутах 3 ромбів. Каталанове тіло та двоїстий многогранник до ікосододекаедра. Зоноедр.

Грань ромботриаконтаедра. Довжини діагоналей утворюють золотий перетин

Анімація показує перетворення куба в ромботриаконтаедр шляхом поділу квадратних граней на 4 квадрати та поділу середніх ребер на нові ромбічні грані.

Відношення довгої діагоналі до короткої діагоналі кожної грані точно дорівнює золотому перетину, φ, так що гострі кути на кожній грані дорівнюють 2 tan⁻¹(1/φ) = tan⁻¹(2) або приблизно 63,43°. Такий ромб називають золотим.

Як двоїстий до архімедового тіла, є гране-транзитивним, тобто група симетрії тіла діє транзитивно на множині граней. Це означає, що для будь-яких двох граней A і B, є поворот або відбиття, яке переводить грань A в грань B, після якого тіло займає ту саму ділянку простору.

Один із дев'яти реберно-транзитивних опуклих многогранників, а інші — це п'ять платонових тіл, кубооктаедр, ікосододекаедр і ромбододекаедр.

Вершини належать чотирьом платоновим тілам. Містить десять тетраедрів, п'ять кубів, ікосаедр і додекаедр. Центри граней утворюють п'ять октаедрів.

Ромботриаконтаедр можна скласти зі зрізаного октаедра, розділивши шестикутні грані на 3 ромби:

Топологічний ромботриаконтаедр у зрізаному октаедрі

Декартові координати

Нехай $\phi$ — золота пропорція. 12 точок, а саме $(0,\pm 1,\pm \phi )$ та з циклічними перестановками цих координат, є вершинами правильного ікосаедра. Двоїстий до нього правильний додекаедр, ребра якого перетинають ребра ікосаедра під прямим кутом, має вершинами 8 точок $(\pm 1,\pm 1,\pm 1)$, а також 12 точок із координатами $(0,\pm \phi ,\pm 1/\phi )$ та їх циклічними перестановками. Усі 32 точки разом є вершинами ромботриаконтаедра з центром у початку координат. Довжина його ребер становить ${\sqrt {3-\phi }}\approx 1.175\,570\,504\,58$. Його грані мають діагоналі з довжинами $2$ і $2/\phi$.

Розміри

Якщо довжина ребра ромботриаконтаедра дорівнює $a$, площа поверхні, об'єм, радіус $r_{i}$ вписаної сфери (дотичної до кожної з граней ромбічного триаконтаедра) і радіус $r_{m}$ напіввписаної сфери (дотичної до середини кожного ребра), дорівнюють:

${\begin{aligned}S&=12{\sqrt {5}}\,a^{2}&&\approx 26.8328a^{2}\\V&=4{\sqrt {5+2{\sqrt {5}}}}\,a^{3}&&\approx 12.3107a^{3}\\r_{\mathrm {i} }&={\frac {\varphi ^{2}}{\sqrt {1+\varphi ^{2}}}}\,a={\sqrt {1+{\frac {2}{\sqrt {5}}}}}\,a&&\approx 1.37638a\\r_{\mathrm {m} }&=\left(1+{\frac {1}{\sqrt {5}}}\right)\,a&&\approx 1.44721a\end{aligned}}$

де φ — золотий перетин.

Вписана сфера дотикається до граней у їхніх центроїдах. Короткі діагоналі належать тільки ребрам вписаного правильного додекаедра, а довгі — тільки ребрам вписаного ікосаедра.

Розтин

Ромботриаконтаедр можна розділити на 20 золотих ромбоедрів: 10 гострих і 10 тупих.

10	10
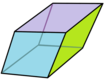Гостра форма	Тупа форма

Ортогональні проєкції

Ромботриаконтаедр має чотири симетричні поєкції: дві з центрами у вершинах, одну — в центрі грані та одну — посередині ребра. У проекція «10» містить «товстий» і «худий» ромби, які разом утворюють неперіодичну мозаїку, звану мозаїкою Пенроуза.

Ортогональні проєкції

Проєктивна симетрія	[2]	[2]	[6]	[10]
Зображення
Двоїсте зображення

Ззірчення

Ромбічний шестиконтаедр

Приклад ззірчень ромботриаконтаедра.

Ромботриаконтаедр має 227 повністю витриманих ззірчень. Ще одним ззірченям ромботриаконтаедра є з'єднання п'яти кубів. Загальна кількість зірок ромбічного триаконтаедра становить 358 833 097.

Споріднені многогранники

Сімейство однорідних ікосаедричних багатогранників

Симетрія: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Двоїсті до однорідних багатогранників
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Цей многогранник є частиною послідовності ромбічних многогранників і мозаїк із [n,3] симетрією групи Коксетера. Куб можна розглядати як ромбічний шестигранник, де ромби також є прямокутниками.

• 
  Сферичний ромботриаконтаедр
• 
  Ромботриаконтаедр зі вписаним тетраедром (червоний) і кубом (жовтий).
  (Натисніть тут, щоб переглянути обертову модель)
• 
  Ромботриаконтаедр зі вписаними додекаедром (синій) та ікосаедром (фіолетовий).
  (Натисніть тут, щоб переглянути обертову модель)
• 
  Повністю зрізаний ромботриаконтаедр

6-куб

Ромботриаконтаедр утворює опуклу оболонку з 32 вершин однієї з проєкцій 6-куба на три виміри.

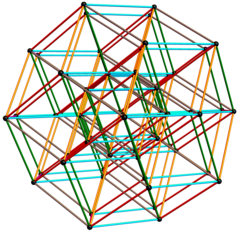Тривимірні базисні вектори [u, v,w]: u = (1, φ, 0, -1, φ, 0): v = (φ, 0, 1, φ, 0, -1): w = (0, 1, φ, 0, -1, φ)

Показано з прихованими внутрішніми краями. 20 із 32 внутрішніх вершин утворюють додекаедр, а решта 12 утворюють ікосаедр.

Використання

Світильник у формі ромботриаконтаедра

Датський дизайнер Гольґер Стрьом використав ромбічнотриаконтаедр як основу для дизайну своєї збірної лампи IQ-light (IQ означає «взаємопереплетені чотирикутники»).

STL-модель ромботриконтаедричної коробки з шести панелей навколо кубічної порожнини — збільште модель, щоб побачити порожнину зсередини

Майстер по дереву Джейн Костік виготовляє скриньки у формі ромботриаконтаедра. Проста конструкція базується не дуже очевидному зв'язку між ромботриаконтаедром і кубом.

«Ball of Whacks» Роджера фон Оеха складається з 30 пластмасових пірамідальних деталей, які містять магніти, ромбічні основи яких у зібраному вигляді головоломки є гранями ромботриаконтаедра, а вершини пірамід збігаються в його центрі.

Ромбічний триаконтаедр використовують як «d30» (тридцятигранний кубик) у деяких рольових іграх тощо.

Крістофер Берд, співавтор «Таємного життя рослин», у травні 1975 року написав статтю для New Age Journal, де популяризує подвійний ікосаедр і додекаедр як «кристалічну структуру Землі», модель «земної (телуричної) енергетичної сітки». Глобус EarthStar Білла Беккера та Бете А. Гаґенс має на меті показати «природну геометрію Землі та геометричний зв'язок між священними місцями, такими як Велика піраміда, Бермудський трикутник та острів Пасхи». Він надрукований у вигляді ромботриаконтаедра на 30 діамантах і складається у вигляді глобуса.

Див. також

• Золотий ромб
• Ромбічна мозаїка^[en]
• Зрізаний ромботриаконтаедр^[en]

Література

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, p. 22, Rhombic triacontahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, p. 285, Rhombic triacontahedron)

Посилання

• Weisstein, Eric W. Ромботриаконтаедр(англ.) на сайті Wolfram MathWorld.
• Rhombic Triacontrahedron — Interactive Polyhedron Model
• Virtual Reality Polyhedra — The Encyclopedia of Polyhedra
• Stellations of Rhombic Triacontahedron
• EarthStar globe — Rhombic Triacontahedral map projection
• IQ-light—Danish designer Holger Strøm's lamp
• Make your own [Архівовано 17 липня 2007 у Wayback Machine.]
• Дерев'яна конструкція коробки у формі ромботриаконтаедра — художник по дереву Джейн Костік
• 120 Rhombic Triacontahedra, 30+12 Rhombic Triacontahedra, і 12 Rhombic Triacontahedra від Шандора Кабаї, The Wolfram Demonstrations Project
• A viper drawn on a rhombic triacontahedron.