Купол (геометрія)

Множина куполів
П'ятисхилий купол (приклад)
Тип	Множина куполів
Символ Шлефлі	{n} || t{n}
Граней	2n+2 : n рівнобедрених трикутників, n прямокутників, 1 правильний n-кутник, 1 2n-кутник
Ребер	5n
Вершин	3n
Характеристика Ейлера	$\chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2$
Позначення	Un (Нотація Конвея для многогранників)
Група симетрії	Cnv, [n], (*nn), порядок 2n (Циклічна симетрія n-Піраміди)
Група поворотів	Cn, [n]+, (nn), порядок n
Дуальний многогранник	?
Властивості	опуклий

Ку́пол (n-схилий купол) — тіло, утворене з'єднанням двох багатокутників, у якому один (основа) має вдвічі більше сторін, порівняно з іншим (верхньою гранню). З'єднання багатокутників здійснюється рівнобедреними трикутниками і прямокутниками.

n-схилий купол — призматоїд, що складається з 2n-кутника (нижня основа купола), правильного n-кутника (верхня грань, що паралельна основі), та бічних граней: n прямокутників та n рівнобедрених трикутників. При чому нижня грань може бути правильним 2n-кутником, або напівправильним 2n-кутником, у якого сторони рівні через одну і всі кути рівні.

Купол можна розглядати як призму, де один з багатокутників наполовину стягнуто попарним об'єднанням вершин.

Куполу можна приписати розширений символ Шлефлі {n} || t{n}, що описує правильний багатокутник {n}, з'єднаний з паралельною йому зрізаною копією, t{n} або {2n}.

Куполи є підкласом призматоїдів.

Його двоїстий многогранник має форму, яка є свого роду поєднанням половини n-стороннього трапецоедра та 2n-гранної піраміди.

Купол має вісь симетрії порядку n, що проходить через центри основ, а також n площин дзеркальної симетрії, що проходять через вісь купола та середини сторін нижньої основи.

Два купола можуть бути з'єднані по їх нижній основі, утворюючи многогранник бікупол.

Куполи і бікуполи існують як нескінченні множини многогранників, так само, як множини пірамід, біпірамід, призм, антипризм, трапецоедрів та ін.

Приклади

Сімейство опуклих куполів

n	2	3	4	5	6	7
Назва	Двосхилий купол	Трисхилий купол	Чотирисхилий купол	П'ятисхилий купол	Шестисхилий купол (плоский)	Семисхилий купол (з неправильними бічними гранями)
Символ Шлефлі	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}	{7} || t{7}
Купол
Пов'язані однорідні багатогранники	Трикутна призма	Кубооктаедр	Ромбокубо- октаедр	Ромбоікосо- додекаедр	Ромботри- шестикутна мозаїка	Ромботри- семикутна мозаїка

Трикутну призму можна вважати «двосхилим куполом» (купол відрізка і квадрата). Якщо бокові грані купола є правильними трикутниками та квадратами, тоді як основа і верхня грань є правильними багатокутниками, купол є многогранником Джонсона. Ці куполи: трисхилий купол, чотирисхилий і п'ятисхилий, можна отримати, взявши зрізи кубооктаедра, ромбокубооктаедра і ромбоікосододекаедра відповідно.

Плоскі «шестикутні куполи» в ромботришестикутній мозаїці

Якщо купол має всі ребра одинакової довжини $a$ (правильногранний) ‒ n = 3, 4, 5, то: Висота купола:

$H={\sqrt {1-{\frac {1}{4}}\cdot \csc ^{2}\left({\frac {\pi }{n}}\right)}}\cdot a$

Радіус описаної сфери:

$R={\sqrt {\frac {7+4\cdot \cos \left({\frac {\pi }{n}}\right)-4\cdot \cos ^{2}\left({\frac {\pi }{n}}\right)}{12-16\cdot \cos ^{2}\left({\frac {\pi }{n}}\right)}}}\cdot a$

Рівносторонній «Шестисхилий купол» є плоскою фігурою. Таким чином, сімейство куполів з правильними гранями існує до n = 5 включно.

Куполи з числом сторін багатокутників n > 5 можна побудувати тільки з неправильними трикутними і прямокутними гранями.

Координати вершин

Визначення купола не вимагає правильності основи і верхньої грані, але зручно розглядати випадки, в яких куполи мають максимальну симетрію, C_nv. В цьому випадку верхня грань є правильним n-кутником, тоді як основа є правильним 2n-кутником, або 2n-кутником з двома різними довжинами сторін (через одну) і тими ж кутами, що й у правильного 2n- кутника.

Розташуємо купол у координатній системі так, щоб його основа лежала в площині Oxy з центром в початку координат, а верхня грань проходила паралельно цій площині на висоті h. Вісь Oz є віссю симетрії порядку n. Пронумеруємо вершини основи числами від V₁ до V_2n, а вершини верхньої грані — числами від A₁ до A_n.

Семисхилий купол. Має 7 рівнобедрених трикутників та 7 прямокутників, Верхня грань — правильний 7-кутник і нижня грань (основа) привильний 14-кутник.

Координати вершин тоді можна записати таким чином:

$A_{k}=\left(r\cdot \cos \left({\frac {2\pi \cdot k}{n}}\right),r\cdot \sin \left({\frac {2\pi \cdot k}{n}}\right),h\right)$

$V_{\left(2k-1\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}\right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}\right),0\right)$

$V_{\left(2k\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}\right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}\right),0\right)$

де k = 1, 2, …, n.

$r={\frac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}$ ‒ радіус описаного кола верхнього багатокутника (правильного n ‒ кутника)

$R={\frac {a}{2\cdot \sin \left({\frac {\pi }{2n}}\right)}}$ ‒ радіус описаного кола нижнього багатокутника (правильного 2n ‒ кутника)

$a$ ‒ довжина ребра багатокутників верхньої та нижньої основ.

h ‒ висота купола

Координати вершин купола, повернутого на деякий кут  $\alpha$ навноло його осі (осі z):

$A_{k}=\left(r\cdot \cos \left({\frac {2\pi \cdot k}{n}}+\alpha \right),r\cdot \sin \left({\frac {2\pi \cdot k}{n}}+\alpha \right),h\right)$

$V_{\left(2k-1\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}+\alpha \right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}+\alpha \right),0\right)$

$V_{\left(2k\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}+\alpha \right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}+\alpha \right),0\right)$

де k = 1, 2, …, n.

Антикуполи

Множина антикуполів
П'ятисхилий антикупол (приклад)
Тип	Множина антикуполів
Символ Шлефлі	s{n} || t{n}
Граней	n рівнобедрених трикутників, 2n різносторонніх трикутників, 1 правильний n-кутник, 1 правильний 2n-кутник
Ребер	6n
Вершин	3n
Характеристика Ейлера	$\chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2$
Позначення	Vn (Нотація Конвея для многогранників)
Група симетрії	Cnv, [1,n], (*nn), порядок 2n
Група поворотів	Cn, [1,n]+, (nn), порядок n
Дуальний многогранник	?
Властивості	опуклий

Антику́пол (n‒ кутний антикупол) — тіло, що складається з правильного 2n-кутника (основа антикупола), правильного n-кутника (верхня грань, що паралельна основі), та 3n трикутників двох типів (n рівнобедрених трикутників та 2n різносторонніх трикутників).

При n = 2, верхня грань вироджується в ребро. Антикуполи є підкласом призматоїдів.

Антикупол має вісь симетрії порядку n, що проходить через центри основ та перпендикулярна їм, а також n площин дзеркальної симетрії, що проходять через вісь многогранника та вершини нижньої основи.

Не можна побудувати n-кутний антикупол, щоб всі його грані були правильними багатокутниками; лише деякі грані можуть бути зроблені правильними.

Сімейство опуклих антикуполів

n	2	3	4	5	6…
Назва	Дигональний антикупол	Трисхилий антикупол	Чотирисхилий антикупол	П'ятисхилий антикупол	Шестисхилий антикупол
Антикупол
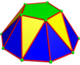
Прозоре зображення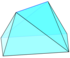
Символ Шлефлі	s{2} || t{2}	s{3} || t{3}	s{4} || t{4}	s{5} || t{5}	s{6} || t{6}
Розгортка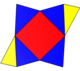

Координати вершин антикупола

Координати вершин n ‒ антикупола можемо отримати з координат вершин n ‒ купола шляхом повороту верхнього n ‒ кутника на кут $\beta ={\frac {\pi }{2n}}$

Розташуємо антикупол у координатній системі так, щоб його основа лежала в площині Oxy з центром в початку координат, а верхня грань проходила паралельно цій площині на висоті h. Вісь Oz є віссю симетрії порядку n. Пронумеруємо вершини основи числами від V₁ до V_2n, а вершини верхньої грані — числами від A₁ до A_n.

Семисхилий антикупол. Має 7 рівнобедрених трикутників та 14 різносторонніх трикутників, Верхня грань — правильний 7-кутник і нижня грань (основа) привильний 14-кутник.

Координати вершин тоді можна записати таким чином:

$A_{k}=\left(r\cdot \cos \left({\frac {2\pi \cdot k}{n}}\pm {\frac {\pi }{2n}}\right),r\cdot \sin \left({\frac {2\pi \cdot k}{n}}\pm {\frac {\pi }{2n}}\right),h\right)$

Поворот n — кутника відбувається по- або проти годинникової стрілки (відповідно знаки «‒» або «+»)

$V_{\left(2k-1\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}\right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}+{\frac {\pi }{2n}}\right),0\right)$

$V_{\left(2k\right)}=\left(R\cdot \cos \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}\right),R\cdot \sin \left({\frac {2\pi \cdot k}{n}}-{\frac {\pi }{2n}}\right),0\right)$

де k = 1, 2, …, n.

$r={\frac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}$ ‒ радіус описаного кола верхнього багатокутника (правильного n ‒ кутника)

$R={\frac {a}{2\cdot \sin \left({\frac {\pi }{2n}}\right)}}$ ‒ радіус описаного кола нижнього багатокутника (правильного 2n ‒ кутника)

$a$ ‒ довжина ребра багатокутників верхньої та нижньої основ.

h ‒ висота антикупола.

Два антикупола можуть бути з'єднані по їх нижній основі, та утворюють многогранник біантикупол.

Антикуполи і біантикуполи існують як нескінченні множини многогранників, так само, як множини пірамід, біпірамід, призм , антипризм , трапецоедрів та ін.

Зірчасті куполи

Сімейство зірчастих куполів

n / d	4	5	7	8
3	{4/3}	{5/3}	{7/3}	{8/3}
5	—	—	{7/5}	{8/5}

Сімейство зірчастих куполоїдів

n / d	3	5	7
2	Перехрещений трикутний куполоїд {3/2}	Пентаграмний куполоїд {5/2}	Гептаграмний куполоїд {7/2}
4	—	Перехрещений пентаграмний куполоїд {5/4}	Перехрещений гептаграмний куполоїд {7/4}

Зірчасті куполи існують для всіх основ {n/d}, де ⁶/₅ < ⁿ/_d < 6 і d непарне. На границях куполи перетворюються на плоскі фігури. Якщо d парне, нижня основа {2n/d} вироджується — ми можемо утворити куполоїд або напівукупол шляхом видалення цієї виродженої грані і дозволивши трикутникам і квадратам з'єднуватися один з одним. Зокрема, тетрагемігексаедр можна розглядати як {3/2}-куполоїд. Усі куполи орієнтовані, тоді як всі куполоїди неорієнтовані. Якщо в куполоїда n/d > 2, трикутники і квадрати не покривають всю основу і на ній залишається тоненька перетинка, яка просто закриває отвір. Таким чином, куполоїди {5/2} і {7/2} на малюнку вище мають перетинки (не заповнені), тоді як куполоїди {5/4} і {7/4} їх не мають.

Висота h купола {n/d} або куполоїда задається формулою

$h={\sqrt {1-{\frac {1}{4\sin ^{2}({\frac {\pi d}{n}})}}}}$.

Зокрема, h = 0 на границях n/d = 6 та n/d = 6/5, і h максимальне при n/d = 2 (трикутна призма, де трикутники розташовані вертикально).

На малюнках вище зірчасті куполи показано в кольорах, щоб підкреслити їх грані — грань n/d-кутника показано червоним, грань 2n/d-кутника показано жовтим, квадрати подано синім кольором, а трикутники — зеленим. Куполоїди мають червоні n/d-кутні грані, жовті квадратні грані, а трикутні грані пофарбовано в блакитний колір, другу ж основу видалено.

Гіперкуполи

Гіперкуполи або многогранні куполи — це сімейство опуклих неоднорідних чотиривимірних многогранників, аналогічних куполам. Основами кожного такого многогранника є правильний многогранник (тривимірний) і його розтягнення .

В таблиці використовується поняття сегментогранник (англ. Segmentochora) — це фігура, що задовольняє таким властивостям:

1. всі вершини розташовані на одній гіперсфері

2. всі вершини розташовані на двох паралельних гіперплощинах

3. всі ребра мають довжину 1

У площині існує два сегментогранники (сегментокутники) — правильний трикутник і квадрат.

У 3-вимірному просторі до них належать піраміди, призми, антипризми, куполи.

Назва	Тетраедричний купол		Кубічний купол		Октаедричний купол		Додекаедричний купол		Шестикутний мозаїчний купол
Символ Шлефлі	{3,3} ∨ rr{3,3}		{4,3} ∨ rr{4,3}		{3,4} ∨ rr{3,4}		{5,3} ∨ rr{5,3}		{6,3} ∨ rr{6,3}
Індекс сегментогранника	K4.23		K4.71		K4.107		K4.152
Радіус описаного кола	1		${\sqrt {\frac {3+{\sqrt {2}}}{2}}}$ $\approx 1.485634$		${\sqrt {2+{\sqrt {2}}}}$ $\approx 1.847759$		$3+{\sqrt {5}}$ $\approx 5.236068$
Малюнок
Головні комірки
Вершин	16		32		30		80		∞
Ребер	42		84		84		210		∞
Граней	42	24 {3} + 18 {4}	80	32 {3} + 48 {4}	82	40 {3} + 42 {4}	194	80 {3} + 90 {4} + 24 {5}	∞
Комірок	16	1 тетраедр 4 трикутні призми 6 трикутних призм 4 трикутні призми 1 кубооктаедр	28	1 куб 6 квадратних призм 12 трикутних призм 8 трикутних пірамід 1 ромбокубооктаедр	28	1 октаэдр 8 трикутних призм 12 трикутних призм 6 квадратних пірамід 1 ромбокубооктаедр	64	1 додекаедр 12 п'ятикутних призм 30 трикутних призм 20 трикутних пірамід 1 ромбоікосододекаедр	∞	1 шестикутна мозаїка ∞ шестикутних призм ∞ трикутних призм ∞ трикутних пірамід 1 ромботришестикутна мозаїка
Пов'язані однорідні 4-вимірні многогранники	Рансінований 5-комірник		Рансінований тесеракт		Рансінований 24-комірник		Рансінований 120-комірник		Рансінований шестикутний мозаїчний стільник

Література

• N.W. Johnson. Convex Polyhedra with Regular Faces // Canad. J. Math. — 1966. — Вип. 18 (30 листопада). — С. 169–200.
• Dr. Richard Klitzing. Symmetry: Culture and Science. — 2000. — Т. 11. — С. 139-181. Архівовано з джерела 19 квітня 2014

Посилання

• Weisstein, Eric W. Cupola(англ.) на сайті Wolfram MathWorld.
• Segmentotopes [Архівовано 13 грудня 2014 у Wayback Machine.]
• Cupola. Polytope Wiki (англ.).