Математичні функції
Лемніскатна функція синуса (червона) та лемніскатна функція косинуса (фіолетова) дійсного аргументу
x
{\displaystyle x}
y
=
sin
(
π
x
ω
)
{\displaystyle y=\sin(\pi x\omega )}
У математиці лемніскатна еліптична функція — це еліптична функція , що пов'язана з довжиною дуги лемніскати Бернуллі .
Вперше вона була досліджена Джуліо Карло де Тоскі ді Фаньяно [en] Леонардом Ейлером , Карлом Фрідріхом Гаусом та іншими.
Лемніскатні функції синуса та косинуса, для позначення яких зазвичай використовують символи
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
sinlem
{\displaystyle \operatorname {sinlem} }
coslem
{\displaystyle \operatorname {coslem} }
sinlemn
{\displaystyle \operatorname {sinlemn} }
coslemn
{\displaystyle \operatorname {coslemn} }
[1] тригонометричних функцій синуса та косинуса.
У той час як тригонометричний синус пов'язує довжину дуги з довжиною хорди в колі одиничного діаметра
x
2
+
y
2
=
x
{\displaystyle x^{2}+y^{2}=x}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle {\big (}x^{2}+y^{2}{\big )}^{2}=x^{2}-y^{2}}
Періоди лемніскатних функції пов'язані з числом
ϖ
=
2,622
057
…
{\displaystyle \varpi =2{,}622057\dots }
лемніскатною константою , що є відношенням лемніскатного периметра до його діаметра.
Функції
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
квадратну періодичну ґратку [en] гауссовим цілим числам ) з фундаментальними періодами [en]
{
(
1
+
i
)
ϖ
,
(
1
−
i
)
ϖ
}
{\displaystyle {\big \{}(1+{\rm {i}})\varpi ,(1-{\rm {i}})\varpi {\big \}}}
[2] еліптичних функцій Якобі на цій ґратці,
sl
z
=
sn
(
z
;
i
)
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;{\rm {i}})}
cl
z
=
cd
(
z
;
i
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;{\rm {i}})}
Аналогічно, гіперболічні лемніскатичні функції
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
{
2
ϖ
,
2
ϖ
i
}
{\displaystyle {\big \{}{\sqrt {2}}\varpi ,{\sqrt {2}}\varpi {\rm {i}}{\big \}}}
Лемніскатні функції та гіперболічні функції пов'язані з еліптичною функцією Веєрштраса
℘
(
z
;
a
,
0
)
{\displaystyle \wp (z;a,0)}
Лемніскатні функції синуса та косинуса [ ред. | ред. код ] Лемніскатні функції
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
задач Коші :[3]
d
d
z
sl
z
=
(
1
+
sl
2
z
)
cl
z
,
sl
(
0
)
=
0
,
d
d
z
cl
z
=
−
(
1
+
cl
2
z
)
sl
z
,
cl
(
0
)
=
1
,
{\displaystyle {\begin{aligned}&{\frac {\rm {d}}{{\rm {d}}z}}\operatorname {sl} z={\big (}1+\operatorname {sl} ^{2}z{\big )}\operatorname {cl} z,\quad \operatorname {sl} (0)=0,\\&{\frac {\rm {d}}{{\rm {d}}z}}\operatorname {cl} z=-{\big (}1+\operatorname {cl} ^{2}z{\big )}\operatorname {sl} z,\quad \operatorname {cl} (0)=1,\end{aligned}}}
або, еквівалентно, визначити як обернені функції для еліптичного інтеграла , тобто як відображення Шварца–Крістофеля [en] одиничного круга комплексної площини у квадрат з кутами
{
1
2
ϖ
,
1
2
ϖ
i
,
−
1
2
ϖ
,
−
1
2
ϖ
i
}
{\displaystyle {\big \{}{\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi {\rm {i}},-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi {\rm {i}}{\big \}}}
[4]
z
=
∫
0
sl
z
d
t
1
−
t
4
=
∫
cl
z
1
d
t
1
−
t
4
.
{\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}.}
Поза цим квадратом функції можуть бути аналітично продовжені на всю комплексну площину за допомогою серій віддзеркалень .
Для порівняння, функції синуса і косинуса на колі можна визначити, відповідно, як розв'язки задач Коші:
d
d
z
sin
z
=
cos
z
,
sin
(
0
)
=
0
,
d
d
z
cos
z
=
−
sin
z
,
cos
(
0
)
=
1
,
{\displaystyle {\begin{aligned}&{\frac {\rm {d}}{{\rm {d}}z}}\sin z=\cos z,\quad \sin(0)=0,\\&{\frac {\rm {d}}{{\rm {d}}z}}\cos z=-\sin z,\quad \cos(0)=1,\end{aligned}}}
або як обернені функції для відображення з верхньої півплощини в напівнескінченну смугу з дійсними частинами між
−
1
2
π
{\displaystyle -{\tfrac {1}{2}}\pi }
1
2
π
{\displaystyle {\tfrac {1}{2}}\pi }
z
=
∫
0
sin
z
d
t
1
−
t
2
=
∫
cos
z
1
d
t
1
−
t
2
.
{\displaystyle z=\int _{0}^{\sin z}{\frac {{\rm {d}}t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{2}}}}.}
Довжина кривої лемніскати Бернулі [ ред. | ред. код ] Лемніскатні функції синуса та косинуса пов'язують довжину кривої лемніскати з відстанню від кінцевої точки до початку координат. Тригонометричні функції синуса та косинуса аналогічно пов'язують довжину дуги кола одиничного діаметра з відстанню від кінцевої точки до початку координат. Лемніската Бернулі з напівшириною 1 є геометричним місцем точок на площині таких, що добуток відстані від яких до двох фокусних точок
F
1
=
(
−
1
2
,
0
)
{\displaystyle F_{1}={\big (}-{\tfrac {1}{\sqrt {2}}},0{\big )}}
F
2
=
(
1
2
,
0
)
{\displaystyle F_{2}={\big (}{\tfrac {1}{\sqrt {2}}},0{\big )}}
1
2
{\displaystyle {\tfrac {1}{2}}}
плоска крива четвертого порядку [en]
r
2
=
cos
2
θ
{\displaystyle r^{2}=\cos 2\theta }
полярних координатах або рівняння
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle {\big (}x^{2}+y^{2}{\big )}^{2}=x^{2}-y^{2}}
декартових координатах .
Точки на лемніскаті на відстані
r
{\displaystyle r}
початку координат є перетинами кола
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
гіперболи
x
2
−
y
2
=
r
4
{\displaystyle x^{2}-y^{2}=r^{4}}
(
x
(
r
)
,
y
(
r
)
)
=
(
1
2
r
2
(
1
+
r
2
)
,
1
2
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\bigg (}{\sqrt {{\tfrac {1}{2}}r^{2}{\big (}1+r^{2}{\big )}}},{\sqrt {{\tfrac {1}{2}}r^{2}{\big (}1-r^{2}{\big )}}}{\bigg )}.}
Використовуючи параметризацію з
r
∈
[
0
,
1
]
{\displaystyle r\in [0,1]}
довжину кривої від початку координат до точки
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
[5]
∫
0
r
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
0
r
(
1
+
2
t
2
)
2
2
(
1
+
t
2
)
+
(
1
−
2
t
2
)
2
2
(
1
−
t
2
)
d
t
=
∫
0
r
d
t
1
−
t
4
=
arcsl
r
.
{\displaystyle \int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,{\rm {d}}t=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\,{\rm {d}}t=\int _{0}^{r}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}=\operatorname {arcsl} r.}
Аналогічно, довжина кривої від точки
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
∫
r
1
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
r
1
d
t
1
−
t
4
=
arccl
r
=
1
2
ϖ
−
arcsl
r
.
{\displaystyle \int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}{\rm {d}}t=\int _{r}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.}
Або у зворотньому порядку, за допомогою лемніскатних функцій синуса та косинуса визначають відстань від початку координат як функції довжини кривої, відповідно від початку координат до точки
(
1
,
0
)
{\displaystyle (1,0)}
r
=
cos
θ
{\displaystyle r=\cos \theta }
x
2
+
y
2
=
x
{\displaystyle x^{2}+y^{2}=x}
(
x
(
r
)
,
y
(
r
)
)
=
(
r
2
,
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}r^{2},{\sqrt {r^{2}{\bigl (}1-r^{2}{\bigr )}}}{\biggr )}.}
Лемніскатний інтеграл та лемніскатні функції задовольняють тотожності подвійного аргументу, яку запропонував Фаньяно у 1718 році:[6]
∫
0
z
d
t
1
−
t
4
=
2
∫
0
u
d
t
1
−
t
4
,
{\displaystyle \int _{0}^{z}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}=2\int _{0}^{u}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}},}
якщо
z
=
2
u
1
−
u
4
1
+
u
4
та
0
≤
u
≤
2
−
1
.
{\displaystyle z={\frac {2u{\sqrt {1-u^{4}}}}{1+u^{4}}}\quad {\text{та}}\quad 0\leq u\leq {\sqrt {{\sqrt {2}}-1}}.}
Пізніше математики узагальнили цей результат.
За аналогією з конструктивними багатокутниками [en]
n
{\displaystyle n}
циркуль та лінійку тоді й лише тоді, коли
n
{\displaystyle n}
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k
{\displaystyle k}
p
j
{\displaystyle p_{j}}
числа Ферма .[7] Нільсом Абелем в 1827—1828 роках, а «достатність» була доведена Майклом Розеном [en] [8]
n
{\displaystyle n}
log
2
φ
(
n
)
{\displaystyle \log _{2}\varphi (n)}
φ
(
n
)
{\displaystyle \varphi (n)}
функцією Ейлера ).
Лемніската не вважається намальованою, а теорема відноситься лише до побудови точок поділу.
Нехай
r
j
=
sl
2
j
ϖ
n
{\displaystyle r_{j}=\operatorname {sl} {\tfrac {2j\varpi }{n}}}
n
{\displaystyle n}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
(
r
j
1
+
r
j
2
2
,
(
−
1
)
⌊
1
2
−
2
j
n
⌋
r
j
1
−
r
j
2
2
)
,
j
∈
{
1
,
2
,
…
,
n
}
,
{\displaystyle \left(r_{j}{\sqrt {\frac {1+r_{j}^{2}}{2}}},(-1)^{\left\lfloor {\frac {1}{2}}-{\frac {2j}{n}}\right\rfloor }r_{j}{\sqrt {\frac {1-r_{j}^{2}}{2}}}\right),\quad j\in \{1,2,\ldots ,n\},}
де
⌊
⋅
⌋
{\displaystyle \lfloor \cdot \rfloor }
функція підлоги .
Нижче наведені деякі частинні значення для
sl
2
ϖ
n
{\displaystyle \operatorname {sl} {\tfrac {2\varpi }{n}}}
Довжина дуги кривої пружного деформування [ ред. | ред. код ] Лемніскатна функція синуса пов'язує довжину дуги з координатою
x
{\displaystyle x}
Обернена функція лемніскати синуса описує довжину
s
{\displaystyle s}
x
{\displaystyle x}
кривої пружного деформування [en] [9]
y
{\displaystyle y}
y
=
∫
x
1
t
2
d
t
1
−
t
4
,
s
=
arcsl
x
=
∫
0
x
d
t
1
−
t
4
.
{\displaystyle y=\int _{x}^{1}{\frac {t^{2}\,{\rm {d}}t}{\sqrt {1-t^{4}}}},\quad s=\operatorname {arcsl} x=\int _{0}^{x}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}.}
Крива пружного деформування є розв'язком задачі, яку запропонував Якоб Бернуллі в 1691 для опису форм ідеалізованого гнучкого стержня, зафіксованого у вертикальному положенні у нижньому кінці і який відтягується від верхнього кінця до горизонтально положення.
Запропонований Бернуллі розв'язок став основою теорії балки Ейлера--Бернуллі , яка була розроблена Ейлером в 18 столітті.
Лемніскатна константа [ ред. | ред. код ] Функція
sl
z
{\displaystyle \operatorname {sl} z}
[10]
(
1
+
i
)
ϖ
{\displaystyle (1+{\rm {i}})\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-{\rm {i}})\varpi }
Лемніскатні функції мають мінімальний період
2
ϖ
{\displaystyle 2\varpi }
(
1
+
i
)
ϖ
{\displaystyle (1+{\rm {i}})\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-{\rm {i}})\varpi }
ϖ
{\displaystyle \varpi }
лемніскатною константою ,[11] [12]
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2
∫
0
∞
d
t
1
+
t
4
=
∫
0
1
d
t
t
−
t
3
=
4
∫
0
∞
(
1
+
t
4
4
−
t
)
d
t
=
2
2
∫
0
1
1
−
t
4
4
d
t
=
3
∫
0
1
1
−
t
4
d
t
=
2
K
(
i
)
=
1
2
B
(
1
4
,
1
2
)
=
Γ
(
1
/
4
)
2
2
2
π
=
π
e
β
′
(
0
)
=
2
−
2
4
ζ
(
3
/
4
)
2
ζ
(
1
/
4
)
2
=
2,622
05
75542
92119
81046
48395
89891
11941
…
,
{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {{\rm {d}}t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {{\rm {d}}t}{\sqrt {t-t^{3}}}}\\&=4\int _{0}^{\infty }\left({\sqrt[{4}]{1+t^{4}}}-t\right)\,{\rm {d}}t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {{\rm {d}}t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,{\rm {d}}t\\&=2K({\rm {i}})={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\sqrt {\pi }}{\rm {e}}^{\beta '(0)}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\&=2{,}62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}
де
K
{\displaystyle K}
повний еліптичний інтеграл першого роду з модулем
k
{\displaystyle k}
B
{\displaystyle {\rm {B}}}
бета-функція ,
γ
{\displaystyle \gamma }
гамма-функція ,
β
′
{\displaystyle \beta '}
ς
{\displaystyle \varsigma }
дзета-функція Рімана . Однак іноді величину
2
ϖ
{\displaystyle 2\varpi }
ϖ
/
2
{\displaystyle \varpi /2}
[13] [14] [15] [16] [17]
ϖ
{\displaystyle \varpi }
периметра лемніскати Бернуллі до її діаметра .
Трансцендентність лемніскатної константи була доведена Теодором Шнайдером [en] [18] Григорій Чудновський [en]
π
{\displaystyle \pi }
ϖ
{\displaystyle \varpi }
алгебраїчно незалежними над полем
Q
{\displaystyle \mathbb {Q} }
[19] [20]
G
=
ϖ
/
π
=
0,834
6
…
{\displaystyle G=\varpi /\pi =0{,}8346\ldots }
константою Гаусса .
Геометричне зображення констант
ϖ
/
2
{\displaystyle \varpi /2}
ϖ
/
2
{\displaystyle \varpi /{\sqrt {2}}}
Лемніскатні функції задовольняють основне співвідношення
cl
z
=
sl
(
1
2
ϖ
−
z
)
.
{\displaystyle \operatorname {cl} z=\operatorname {sl} {\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}.}
Крім того, константа
ϖ
{\displaystyle \varpi }
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
π
n
:=
B
(
1
n
,
1
n
)
{\displaystyle \pi _{n}:={\rm {B}}{\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}
x
n
+
y
n
=
1
{\displaystyle x^{n}+y^{n}=1}
2
∫
0
1
1
−
x
n
n
d
x
=
1
n
π
n
.
{\displaystyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\,{\rm {d}}x={\tfrac {1}{n}}\pi _{n}.}
1
4
π
4
=
1
2
ϖ
{\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi }
У 1738 році Ейлер відкрив, що для кривої пружного деформування:[21]
arc
length
⋅
height
=
∫
0
1
d
x
1
−
x
4
⋅
∫
0
1
x
2
d
x
1
−
x
4
=
ϖ
2
⋅
π
2
ϖ
=
π
4
.
{\displaystyle {\begin{aligned}\operatorname {arc} \operatorname {length} \cdot \operatorname {height} =\int _{0}^{1}{\frac {{\rm {d}}x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\,{\rm {d}}x}{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}.\end{aligned}}}
Формула Вієта для числа
π
{\displaystyle \pi }
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
.
{\displaystyle {\begin{aligned}{\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots .\end{aligned}}}
Аналогічна формула для
ϖ
{\displaystyle \varpi }
[22]
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
.
{\displaystyle {\begin{aligned}{\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}/{\sqrt {\frac {1}{2}}}}}}}\cdots .\end{aligned}}}
Формула Валіса для
π
{\displaystyle \pi }
π
2
=
∏
n
=
1
∞
(
1
+
1
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
(
2
1
⋅
2
3
)
(
4
3
⋅
4
5
)
(
6
5
⋅
6
7
)
⋯
.
{\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}\\&=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots .\end{aligned}}}
Аналогічна формула для
ϖ
{\displaystyle \varpi }
[23]
ϖ
2
=
∏
n
=
1
∞
(
1
+
1
2
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
4
n
−
1
4
n
−
2
⋅
4
n
4
n
+
1
)
=
=
(
3
2
⋅
4
5
)
(
7
6
⋅
8
9
)
(
11
10
⋅
12
13
)
⋯
.
{\displaystyle {\begin{aligned}{\frac {\varpi }{2}}&=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)=\\&={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots .\end{aligned}}}
Пов'язаною з цим результатом є формула:
ϖ
π
=
∏
n
=
1
∞
(
4
n
−
1
4
n
⋅
4
n
+
2
4
n
+
1
)
=
(
3
4
⋅
6
5
)
(
7
8
⋅
10
9
)
(
11
12
⋅
14
13
)
⋯
.
{\displaystyle {\begin{aligned}{\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots .\end{aligned}}}
Нескінченний ряд для
ϖ
/
π
{\displaystyle \varpi /\pi }
[24]
ϖ
π
=
∑
n
=
0
∞
(
−
1
)
n
∏
k
=
1
n
(
2
k
−
1
)
2
(
2
k
)
2
=
1
−
1
2
2
2
+
1
2
⋅
3
2
2
2
⋅
4
2
−
1
2
⋅
3
2
⋅
5
2
2
2
⋅
4
2
⋅
6
2
+
⋯
.
{\displaystyle {\begin{aligned}{\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots .\end{aligned}}}
Формула Мачіна [en]
π
{\displaystyle \pi }
1
4
π
=
4
arctg
1
5
−
arctg
1
239
{\displaystyle {\tfrac {1}{4}}\pi =4\operatorname {arctg} {\tfrac {1}{5}}-\operatorname {arctg} {\tfrac {1}{239}}}
π
{\displaystyle \pi }
1
4
π
=
arctg
1
2
+
arctg
1
3
.
{\displaystyle {\tfrac {1}{4}}\pi =\operatorname {arctg} {\tfrac {1}{2}}+\operatorname {arctg} {\tfrac {1}{3}}.}
ϖ
{\displaystyle \varpi }
[15]
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
.
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}.}
[25]
ϖ
=
2
−
1
/
2
π
(
∑
n
∈
Z
e
−
π
n
2
)
2
=
2
1
/
4
π
e
−
π
/
12
(
∑
n
∈
Z
(
−
1
)
n
e
−
π
p
n
)
2
,
{\displaystyle {\begin{aligned}\varpi =2^{-1/2}\pi \left(\sum _{n\in \mathbb {Z} }{\rm {e}}^{-\pi n^{2}}\right)^{2}=2^{1/4}\pi {\rm {e}}^{-\pi /12}\left(\sum _{n\in \mathbb {Z} }(-1)^{n}{\rm {e}}^{-\pi p_{n}}\right)^{2},\end{aligned}}}
де
p
n
=
(
3
n
2
−
n
)
/
2
{\displaystyle p_{n}=(3n^{2}-n)/2}
n
≥
1
{\displaystyle n\geq 1}
п'ятикутне число ), або з використанням середнього арифметико-геометричного
M
{\displaystyle \operatorname {M} }
ϖ
=
π
M
(
1
,
2
)
.
{\displaystyle {\begin{aligned}\varpi ={\frac {\pi }{\operatorname {M} {\big (}1,{\sqrt {2}}{\big )}}}.\end{aligned}}}
У дусі аналогічному до базельської задачі можна записати наступну формулу:
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
=
G
4
(
i
)
=
ϖ
4
15
,
{\displaystyle {\begin{aligned}\sum _{z\in \mathbb {Z} [{\rm {i}}]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}({\rm {i}})={\frac {\varpi ^{4}}{15}},\end{aligned}}}
де
Z
[
i
]
{\displaystyle \mathbb {Z} [{\rm {i}}]}
гауссові числа ,
G
4
(
τ
)
{\displaystyle G_{4}(\tau )}
ряд Ейзенштейна з вагою 4.[26]
Нулі, полюси і симетрії [ ред. | ред. код ] При зсуві на
1
2
ϖ
{\displaystyle {\tfrac {1}{2}}\varpi }
cl
{\displaystyle \operatorname {cl} }
sl
{\displaystyle \operatorname {sl} }
1
2
i
ϖ
{\displaystyle {\tfrac {1}{2}}{\rm {i}}\varpi }
взаємооберненими :[27]
cl
(
z
±
1
2
ϖ
)
=
∓
sl
z
,
cl
(
z
±
1
2
i
ϖ
)
=
∓
i
sl
z
,
sl
(
z
±
1
2
ϖ
)
=
±
cl
z
,
sl
(
z
±
1
2
i
ϖ
)
=
±
i
cl
z
.
{\displaystyle {\begin{alignedat}{3}&\operatorname {cl} {\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}=\mp \operatorname {sl} z,\quad &&\operatorname {cl} {\bigl (}z\pm {\tfrac {1}{2}}{\rm {i}}\varpi {\bigr )}={\frac {\mp {\rm {i}}}{\operatorname {sl} z}},\\&\operatorname {sl} {\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}=\pm \operatorname {cl} z,\quad &&\operatorname {sl} {\bigl (}z\pm {\tfrac {1}{2}}{\rm {i}}\varpi {\bigr )}={\frac {\pm {\rm {i}}}{\operatorname {cl} z}}.\end{alignedat}}}
Подвоєння цих зсувів одиничними елементами гауссових цілих чисел кратних
ϖ
{\displaystyle \varpi }
±
ϖ
{\displaystyle \pm \varpi }
±
i
ϖ
{\displaystyle \pm {\rm {i}}\varpi }
інволюції ):
cl
(
z
+
ϖ
)
=
cl
(
z
+
i
ϖ
)
=
−
cl
z
,
sl
(
z
+
ϖ
)
=
sl
(
z
+
i
ϖ
)
=
−
sl
z
.
{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )=\operatorname {cl} (z+{\rm {i}}\varpi )=-\operatorname {cl} z,\\\operatorname {sl} (z+\varpi )=\operatorname {sl} (z+{\rm {i}}\varpi )=-\operatorname {sl} z.\end{aligned}}}
Як наслідок, обидві функції інваріантні відносно зсуву на парне гаусове ціле число кратне
ϖ
{\displaystyle \varpi }
[28]
(
a
+
b
i
)
ϖ
{\displaystyle (a+b{\rm {i}})\varpi }
a
+
b
=
2
k
{\displaystyle a+b=2k}
a
{\displaystyle a}
b
{\displaystyle b}
k
{\displaystyle k}
cl
(
z
+
(
1
+
i
)
ϖ
)
=
cl
(
z
+
(
1
−
i
)
ϖ
)
=
cl
z
,
sl
(
z
+
(
1
+
i
)
ϖ
)
=
sl
(
z
+
(
1
−
i
)
ϖ
)
=
sl
z
.
{\displaystyle {\begin{aligned}&\operatorname {cl} {\bigl (}z+(1+{\rm {i}})\varpi {\bigr )}=\operatorname {cl} {\bigl (}z+(1-{\rm {i}})\varpi {\bigr )}=\operatorname {cl} z,\\&\operatorname {sl} {\bigl (}z+(1+{\rm {i}})\varpi {\bigr )}=\operatorname {sl} {\bigl (}z+(1-{\rm {i}})\varpi {\bigr )}=\operatorname {sl} z.\end{aligned}}}
Це робить їх еліптичними функціями (двічі періодичні мероморфні функції в комплексній площині) з діагонально-квадратною періодичною ґраткою [en]
(
1
+
i
)
ϖ
{\displaystyle (1+{\rm {i}})\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-{\rm {i}})\varpi }
[29]
Еліптичні функції з періодичною квадратною ґраткою більш симетричні, ніж довільні еліптичні функції, що слідують симетрії ґратки.
Віддзеркалення і повороти на чверть обороту аргументів лемніскатної функції мають прості вирази:
cl
z
¯
=
cl
z
¯
,
sl
z
¯
=
sl
z
¯
,
cl
i
z
=
1
cl
z
,
sl
i
z
=
i
sl
z
.
{\displaystyle {\begin{aligned}&\operatorname {cl} {\bar {z}}={\overline {\operatorname {cl} z}},\\&\operatorname {sl} {\bar {z}}={\overline {\operatorname {sl} z}},\\&\operatorname {cl} {\rm {i}}z={\frac {1}{\operatorname {cl} z}},\\&\operatorname {sl} {\rm {i}}z={\rm {i}}\operatorname {sl} z.\end{aligned}}}
Функція
sl
{\displaystyle \operatorname {sl} }
нулі в гаусових цілих числах кратних
ϖ
{\displaystyle \varpi }
a
ϖ
+
b
ϖ
i
{\displaystyle a\varpi +b\varpi {\rm {i}}}
a
{\displaystyle a}
b
{\displaystyle b}
полюси у гаусових напівцілих числах кратних
ϖ
{\displaystyle \varpi }
(
a
+
1
2
)
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi {\rm {i}}}
лишком
(
−
1
)
a
−
b
+
1
i
{\displaystyle (-1)^{a-b+1}{\rm {i}}}
cl
{\displaystyle \operatorname {cl} }
sl
{\displaystyle \operatorname {sl} }
cl
z
=
sl
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {cl} z=\operatorname {sl} {\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}}
(
a
+
1
2
)
ϖ
+
b
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +b\varpi {\rm {i}}}
a
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle a\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi {\rm {i}}}
(
−
1
)
a
−
b
i
{\displaystyle (-1)^{a-b}{\rm {i}}}
Оскільки лемніскатний синус є мероморфною функцією, то його можна записати як відношення голоморфних функцій.
Гаусс показав, що функція
sl
{\displaystyle \operatorname {sl} }
[30]
sl
z
=
M
(
z
)
N
(
z
)
,
{\displaystyle {\begin{aligned}\operatorname {sl} z={\frac {M(z)}{N(z)}},\end{aligned}}}
де
M
(
z
)
=
z
∏
α
(
1
−
z
4
α
4
)
,
N
(
z
)
=
∏
β
(
1
−
z
4
β
4
)
.
{\displaystyle {\begin{aligned}M(z)=z\prod _{\alpha }\left(1-{\frac {z^{4}}{\alpha ^{4}}}\right),\quad N(z)=\prod _{\beta }\left(1-{\frac {z^{4}}{\beta ^{4}}}\right).\end{aligned}}}
Тут,
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
sl
{\displaystyle \operatorname {sl} }
Re
z
>
0
{\displaystyle \operatorname {Re} z>0}
Im
z
≥
0
{\displaystyle \operatorname {Im} z\geq 0}
ln
N
(
ϖ
)
=
π
/
2
{\displaystyle \ln N(\varpi )=\pi /2}
[31] [32]
Існують також нескінченні ряди, що відображають розподіл нулів і полюсів функції
sl
{\displaystyle \operatorname {sl} }
[33] [33] [34]
1
sl
z
=
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
n
ϖ
+
k
ϖ
i
,
sl
z
=
−
i
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
(
n
+
1
/
2
)
ϖ
+
(
k
+
1
/
2
)
ϖ
i
.
{\displaystyle {\begin{aligned}&{\frac {1}{\operatorname {sl} z}}=\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+n\varpi +k\varpi {\rm {i}}}},\\&\operatorname {sl} z=-{\rm {i}}\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+(n+1/2)\varpi +(k+1/2)\varpi {\rm {i}}}}.\end{aligned}}}
Тотожність піфагорійського типу [ ред. | ред. код ] Криві
x
2
⨁
y
2
=
a
{\displaystyle x^{2}\bigoplus y^{2}=a}
a
{\displaystyle a}
a
{\displaystyle a}
a
{\displaystyle a}
a
=
±
{\displaystyle a=\pm }
a
=
∞
{\displaystyle a=\infty }
Лемніскатні функції задовольняють тотожність піфагорійського типу:
cl
2
z
+
sl
2
z
+
cl
2
z
sl
2
z
=
1.
{\displaystyle {\begin{aligned}\operatorname {cl} ^{2}z+\operatorname {sl} ^{2}z+\operatorname {cl} ^{2}z\operatorname {sl} ^{2}z=1.\end{aligned}}}
Як результат,
(
x
,
y
)
=
(
cl
t
,
sl
t
)
{\displaystyle (x,y)=(\operatorname {cl} t,\operatorname {sl} t)}
кривої четвертого порядку [en]
x
2
+
y
2
+
x
2
y
2
=
1
{\displaystyle x^{2}+y^{2}+x^{2}y^{2}=1}
Цю тотожність можна також представити як[35]
(
1
+
cl
2
z
)
(
1
+
sl
2
z
)
=
2
,
cl
2
z
=
1
−
sl
2
z
1
+
sl
2
z
,
sl
2
z
=
1
−
cl
2
z
1
+
cl
2
z
.
{\displaystyle {\begin{aligned}&{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}{\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}=2,\\&\operatorname {cl} ^{2}z={\frac {1-\operatorname {sl} ^{2}z}{1+\operatorname {sl} ^{2}z}},\quad \operatorname {sl} ^{2}z={\frac {1-\operatorname {cl} ^{2}z}{1+\operatorname {cl} ^{2}z}}.\end{aligned}}}
Позначивши оператор тангенса суми як
a
⊕
b
:=
tg
(
arctg
a
+
arctg
b
)
{\displaystyle a\oplus b:=\operatorname {tg} (\operatorname {arctg} a+\operatorname {arctg} b)}
cl
2
z
⊕
sl
2
z
=
1.
{\displaystyle {\begin{aligned}\operatorname {cl} ^{2}z\oplus \operatorname {sl} ^{2}z=1.\end{aligned}}}
Похідні та інтеграли [ ред. | ред. код ] Похідні:
d
d
z
cl
z
=
cl
′
z
=
−
(
1
+
cl
2
z
)
sl
z
=
−
2
sl
z
sl
2
z
+
1
,
cl
′
2
z
=
1
−
c
l
4
z
,
d
d
z
sl
z
=
sl
′
z
=
(
1
+
sl
2
z
)
cl
z
=
2
cl
z
cl
2
z
+
1
,
sl
′
2
z
=
1
−
sl
4
z
.
{\displaystyle {\begin{aligned}&{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl} 'z=-{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}\operatorname {sl} z=-{\frac {2\operatorname {sl} z}{\operatorname {sl} ^{2}z+1}},\\&\operatorname {cl} '^{2}z=1-\operatorname {cl^{4}} z,\\&{\frac {\rm {d}}{{\rm {d}}z}}\operatorname {sl} z=\operatorname {sl} 'z={\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}\operatorname {cl} z={\frac {2\operatorname {cl} z}{\operatorname {cl} ^{2}z+1}},\\&\operatorname {sl} '^{2}z=1-\operatorname {sl} ^{4}z.\end{aligned}}}
Другі похідні лемніскатних функцій синуса і косинуса є їх від'ємними подвійними кубами:
d
2
d
z
2
cl
z
=
−
2
cl
3
z
,
d
2
d
z
2
sl
z
=
−
2
sl
3
z
.
{\displaystyle {\begin{aligned}{\frac {{\rm {d}}^{2}}{{\rm {d}}z^{2}}}\operatorname {cl} z=-2\operatorname {cl} ^{3}z,\\{\frac {{\rm {d}}^{2}}{{\rm {d}}z^{2}}}\operatorname {sl} z=-2\operatorname {sl} ^{3}z.\end{aligned}}}
Інтеграли від лемніскатні функції виражаються через функцію арктангенс:
∫
cl
z
d
z
=
arctg
sl
z
+
C
,
∫
sl
z
d
z
=
−
arctg
cl
z
+
C
.
{\displaystyle {\begin{aligned}&\int \operatorname {cl} z\,{\rm {d}}z=\operatorname {arctg} \operatorname {sl} z+C,\\&\int \operatorname {sl} z\,{\rm {d}}z=-\operatorname {arctg} \operatorname {cl} z+C.\end{aligned}}}
Сума аргументів і деякі тотожності [ ред. | ред. код ] Як і тригонометричні функції, леменіскатні функції задовольняють тотожності для суми і різниці аргументів.
Оригінальна тотожність, яку використовував Фаньяно для поділу навпіл лемніскати, має наступний вигляд:[36]
sl
(
u
+
v
)
=
sl
u
sl
′
v
+
sl
v
sl
′
u
1
+
sl
2
u
sl
2
v
.
{\displaystyle {\begin{aligned}\operatorname {sl} (u+v)={\frac {\operatorname {sl} u\operatorname {sl} 'v+\operatorname {sl} v\operatorname {sl} 'u}{1+\operatorname {sl} ^{2}u\operatorname {sl} ^{2}v}}.\end{aligned}}}
З використанням похідних і тотожності піфагорійсього типу можна записати тотожність Фаньяно в термінах функцій
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
тангенса суми
a
⊕
b
:=
tg
(
arctg
a
+
arctg
b
)
{\displaystyle a\oplus b:=\operatorname {tg} (\operatorname {arctg} a+\operatorname {arctg} b)}
a
⊖
b
:=
a
⊕
(
−
b
)
{\displaystyle a\ominus b:=a\oplus (-b)}
[37]
cl
(
u
+
v
)
=
cl
u
cl
v
⊖
sl
u
sl
v
=
cl
u
cl
v
−
sl
u
sl
v
1
+
sl
u
cl
u
sl
v
cl
v
,
cl
(
u
−
v
)
=
cl
u
cl
v
⊕
sl
u
sl
v
,
sl
(
u
+
v
)
=
sl
u
cl
v
⊕
cl
u
sl
v
=
sl
u
cl
v
+
cl
u
sl
v
1
−
sl
u
cl
u
sl
v
cl
v
,
sl
(
u
−
v
)
=
sl
u
cl
v
⊖
cl
u
sl
v
.
{\displaystyle {\begin{aligned}&\operatorname {cl} (u+v)=\operatorname {cl} u\operatorname {cl} v\ominus \operatorname {sl} u\operatorname {sl} v={\frac {\operatorname {cl} u\operatorname {cl} v-\operatorname {sl} u\operatorname {sl} v}{1+\operatorname {sl} u\operatorname {cl} u\operatorname {sl} v\operatorname {cl} v}},\\&\operatorname {cl} (u-v)=\operatorname {cl} u\operatorname {cl} v\oplus \operatorname {sl} u\ \operatorname {sl} v,\\&\operatorname {sl} (u+v)=\operatorname {sl} u\operatorname {cl} v\oplus \operatorname {cl} u\operatorname {sl} v={\frac {\operatorname {sl} u\operatorname {cl} v+\operatorname {cl} u\operatorname {sl} v}{1-\operatorname {sl} u\operatorname {cl} u\operatorname {sl} v\operatorname {cl} v}},\\&\operatorname {sl} (u-v)=\operatorname {sl} u\operatorname {cl} v\ominus \operatorname {cl} u\operatorname {sl} v.\end{aligned}}}
Вони нагадують відповідні тригонометричні аналоги :
cos
(
u
±
v
)
=
cos
u
cos
v
∓
sin
u
sin
v
,
sin
(
u
±
v
)
=
sin
u
cos
v
±
cos
u
sin
v
.
{\displaystyle {\begin{aligned}\cos(u\pm v)=\cos u\cos v\mp \sin u\sin v,\\\sin(u\pm v)=\sin u\cos v\pm \cos u\sin v.\end{aligned}}}
Формули половинного аргументу:
cl
2
1
2
x
=
1
+
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
,
sl
2
1
2
x
=
1
−
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
.
{\displaystyle {\begin{aligned}\operatorname {cl} ^{2}{\tfrac {1}{2}}x={\frac {1+\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}},\\\operatorname {sl} ^{2}{\tfrac {1}{2}}x={\frac {1-\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}}.\end{aligned}}}
Формули подвійного аргументу:[38]
cl
2
x
=
−
1
+
2
cl
2
x
+
cl
4
x
1
+
2
cl
2
x
−
cl
4
x
,
sl
2
x
=
2
sl
x
cl
x
1
+
sl
2
x
1
+
sl
4
x
.
{\displaystyle {\begin{aligned}&\operatorname {cl} 2x={\frac {-1+2\operatorname {cl} ^{2}x+\operatorname {cl} ^{4}x}{1+2\operatorname {cl} ^{2}x-\operatorname {cl} ^{4}x}},\\&\operatorname {sl} 2x=2\operatorname {sl} x\operatorname {cl} x{\frac {1+\operatorname {sl} ^{2}x}{1+\operatorname {sl} ^{4}x}}.\end{aligned}}}
Формули потрійного аргументу:[38]
cl
3
x
=
−
3
cl
x
+
6
cl
5
x
+
cl
9
x
1
+
6
cl
4
x
−
3
cl
8
x
,
sl
3
x
=
3
sl
x
−
6
sl
5
x
−
sl
9
x
1
+
6
sl
4
x
−
3
sl
8
x
.
{\displaystyle {\begin{aligned}&\operatorname {cl} 3x={\frac {-3\operatorname {cl} x+6\operatorname {cl} ^{5}x+\operatorname {cl} ^{9}x}{1+6\operatorname {cl} ^{4}x-3\operatorname {cl} ^{8}x}},\\&\operatorname {sl} 3x={\frac {3\operatorname {sl} x-6\operatorname {sl} ^{5}x-\operatorname {sl} ^{9}x}{1+6\operatorname {sl} ^{4}x-3\operatorname {sl} ^{8}x}}.\end{aligned}}}
Лемнатомні многочлени [ ред. | ред. код ] Нехай
L
{\displaystyle L}
ґратка вигляду:
L
=
Z
(
1
+
i
)
ϖ
+
Z
(
1
−
i
)
ϖ
.
{\displaystyle {\begin{aligned}L=\mathbb {Z} (1+{\rm {i}})\varpi +\mathbb {Z} (1-{\rm {i}})\varpi .\end{aligned}}}
Крім того, нехай
K
=
Q
(
i
)
{\displaystyle K=\mathbb {Q} ({\rm {i}})}
O
=
Z
[
i
]
{\displaystyle {\mathcal {O}}=\mathbb {Z} [{\rm {i}}]}
z
∈
C
{\displaystyle z\in \mathbb {C} }
β
=
m
+
i
n
{\displaystyle \beta =m+{\rm {i}}n}
γ
=
m
′
+
i
n
′
{\displaystyle {\gamma }=m'+{\rm {i}}n'}
m
,
n
,
m
′
,
n
′
∈
Z
{\displaystyle m,n,m',n'\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
m
′
+
n
′
{\displaystyle m'+n'}
γ
≡
1
m
o
d
2
(
1
+
i
)
{\displaystyle {\gamma }\equiv 1\ {\rm {mod}}\ 2(1+{\rm {i}})}
sl
β
z
=
M
β
(
sl
z
)
{\displaystyle \operatorname {sl} \beta z=M_{\beta }(\operatorname {sl} z)}
M
β
(
x
)
=
i
ε
x
P
β
(
x
4
)
Q
β
(
x
4
)
{\displaystyle {\begin{aligned}M_{\beta }(x)={\rm {i}}^{\varepsilon }x{\frac {P_{\beta }(x^{4})}{Q_{\beta }(x^{4})}}\end{aligned}}}
для деяких взаємно простих многочленів
P
β
(
x
)
,
Q
β
(
x
)
∈
O
[
x
]
{\displaystyle P_{\beta }(x),Q_{\beta }(x)\in {\mathcal {O}}[x]}
ε
∈
{
0
,
1
,
2
,
3
}
{\displaystyle \varepsilon \in \{0,1,2,3\}}
[39]
x
P
β
(
x
4
)
=
∏
γ
|
β
Λ
γ
(
x
)
,
{\displaystyle {\begin{aligned}xP_{\beta }(x^{4})=\prod _{\gamma |\beta }\Lambda _{\gamma }(x),\end{aligned}}}
та
Λ
β
(
x
)
=
∏
[
α
]
∈
(
O
/
β
O
)
×
(
x
−
sl
α
δ
β
)
,
{\displaystyle {\begin{aligned}\Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta }),\end{aligned}}}
де
δ
β
{\displaystyle \delta _{\beta }}
β
{\displaystyle \beta }
скруту (тобто
[
δ
β
]
∈
(
1
/
β
)
L
{\displaystyle [\delta _{\beta }]\in (1/\beta )L}
[
δ
β
]
∈
(
1
/
β
)
L
/
L
{\displaystyle [\delta _{\beta }]\in (1/\beta )L/L}
(
1
/
β
)
L
/
L
{\displaystyle (1/\beta )L/L}
O
{\displaystyle {\mathcal {O}}}
модуль ).
Прикладами генераторів
β
{\displaystyle \beta }
2
ϖ
/
β
{\displaystyle 2\varpi /\beta }
(
1
+
i
)
ϖ
/
β
{\displaystyle (1+{\rm {i}})\varpi /\beta }
Λ
β
(
x
)
∈
O
[
x
]
{\displaystyle \Lambda _{\beta }(x)\in {\mathcal {O}}[x]}
β
{\displaystyle \beta }
|
(
O
/
β
O
)
×
|
{\displaystyle \left|({\mathcal {O}}/\beta {\mathcal {O}})^{\times }\right|}
K
{\displaystyle \mathbb {K} }
многочлену поділу кола ,[40]
Φ
n
(
x
)
=
∏
[
a
]
∈
(
Z
/
n
Z
)
×
(
x
−
e
2
a
π
i
/
n
)
.
{\displaystyle {\begin{aligned}\Phi _{n}(x)=\prod _{[a]\in (\mathbb {Z} /n\mathbb {Z} )^{\times }}\left(x-{\rm {e}}^{2a\pi {\rm {i}}/n}\right).\end{aligned}}}
β
{\displaystyle \beta }
Λ
β
(
x
)
{\displaystyle \Lambda _{\beta }(x)}
мінімальним многочленом для
sl
δ
β
{\displaystyle \operatorname {sl} \delta _{\beta }}
K
[
x
]
{\displaystyle \mathbb {K} [x]}
sl
(
2
ϖ
/
5
)
{\displaystyle \operatorname {sl} (2\varpi /5)}
sl
(
(
1
+
i
)
ϖ
/
5
)
)
{\displaystyle \operatorname {sl} ((1+{\rm {i}})\varpi /5))}
K
[
x
]
{\displaystyle \mathbb {K} [x]}
Λ
5
(
x
)
=
x
16
+
52
x
12
−
26
x
8
−
12
x
4
+
1
,
{\displaystyle {\begin{aligned}\Lambda _{5}(x)=x^{16}+52x^{12}-26x^{8}-12x^{4}+1,\end{aligned}}}
та[41]
sl
2
ϖ
5
=
−
13
+
6
5
+
2
85
−
38
5
4
{\displaystyle {\begin{aligned}\operatorname {sl} {\frac {2\varpi }{5}}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}}\end{aligned}}}
(еквівалентний вираз наведено в таблиці нижче). Іншим прикладом є[40]
Λ
−
1
+
2
i
(
x
)
=
x
4
−
1
+
2
i
,
{\displaystyle {\begin{aligned}\Lambda _{-1+2{\rm {i}}}(x)=x^{4}-1+2{\rm {i}},\end{aligned}}}
що є мінімальним многочленом для
sl
(
2
ϖ
/
(
−
1
+
2
i
)
)
{\displaystyle \operatorname {sl} (2\varpi /(-1+2{\rm {i}}))}
sl
(
(
1
+
i
)
ϖ
/
(
−
1
+
2
i
)
)
=
sl
(
(
1
−
3
i
)
ϖ
/
5
)
{\displaystyle \operatorname {sl} ((1+{\rm {i}})\varpi /(-1+2{\rm {i}}))=\operatorname {sl} ((1-3{\rm {i}})\varpi /5)}
K
[
x
]
{\displaystyle \mathbb {K} [x]}
Так само, як і для тригонометричних функцій, значення лемніскатних функцій можна обчислити для поділів лемніскати на
n
{\displaystyle n}
n
{\displaystyle n}
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k
{\displaystyle k}
ціле число , і кожне
p
i
{\displaystyle p_{\rm {i}}}
прості числа Ферма .[42]
n
{\displaystyle n}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
n
{\displaystyle n}
n
≤
20
{\displaystyle n\leq 20}
n
{\displaystyle n}
cl
2
ϖ
n
{\displaystyle \operatorname {cl} {\tfrac {2\varpi }{n}}}
sl
2
ϖ
n
{\displaystyle \operatorname {sl} {\tfrac {2\varpi }{n}}}
2
{\displaystyle 2}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
4
{\displaystyle 4}
0
{\displaystyle 0}
1
{\displaystyle 1}
5
{\displaystyle 5}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1)\left({\sqrt {{\sqrt {5}}+2}}-1\right)}
1
2
2
4
(
5
−
1
)
20
4
+
5
−
1
{\displaystyle {\tfrac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}-1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}}
6
{\displaystyle 6}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
8
{\displaystyle 8}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
10
{\displaystyle 10}
1
2
(
5
4
−
1
)
(
5
+
2
+
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\Bigr )}}
1
2
5
−
2
4
2
(
5
−
5
)
+
1
−
5
{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}+1-{\sqrt {5}}}}}
12
{\displaystyle 12}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
16
{\displaystyle 16}
(
2
4
−
1
)
(
2
+
1
+
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}
(
2
4
−
1
)
(
2
+
1
−
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}
20
{\displaystyle 20}
1
2
5
−
2
4
2
(
5
−
5
)
−
1
+
5
{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}-1+{\sqrt {5}}}}}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\Bigr )}}
Розклад в степеневий ряд функції лемніскати синуса у початку координат має вигляд:[43]
sl
z
=
∑
n
=
0
∞
a
n
z
n
=
z
−
1
10
z
5
+
1
120
z
9
−
11
15600
z
13
+
⋯
,
z
∈
C
,
|
z
|
<
ϖ
2
,
{\displaystyle {\begin{aligned}\operatorname {sl} z=\sum _{n=0}^{\infty }a_{n}z^{n}=z-{\tfrac {1}{10}}z^{5}+{\tfrac {1}{120}}z^{9}-{\tfrac {11}{15600}}z^{13}+\cdots ,\quad z\in \mathbb {C} ,\quad |z|<{\tfrac {\varpi }{\sqrt {2}}},\end{aligned}}}
де коефіцієнти
a
n
{\displaystyle a_{n}}
n
≢
1
(
m
o
d
4
)
⟹
a
n
=
0
,
a
1
=
1
,
∀
n
∈
N
0
:
a
n
+
2
=
−
2
(
n
+
1
)
(
n
+
2
)
∑
i
+
j
+
k
=
n
a
i
a
j
a
k
,
{\displaystyle {\begin{aligned}&n\not \equiv 1\ ({\rm {mod}}\ {4})\implies a_{n}=0,\\&a_{1}=1,\ \forall n\in \mathbb {N} _{0}\colon \ a_{n+2}=-{\frac {2}{(n+1)(n+2)}}\sum _{i+j+k=n}a_{i}a_{j}a_{k},\end{aligned}}}
де
i
+
j
+
k
=
n
{\displaystyle i+j+k=n}
композиції для числа
n
{\displaystyle n}
a
13
{\displaystyle a_{13}}
13
−
2
=
11
{\displaystyle 13-2=11}
11
=
9
+
1
+
1
=
1
+
9
+
1
=
1
+
1
+
9
{\displaystyle 11=9+1+1=1+9+1=1+1+9}
11
=
5
+
5
+
1
=
5
+
1
+
5
=
1
+
5
+
5
{\displaystyle 11=5+5+1=5+1+5=1+5+5}
a
13
=
−
2
12
⋅
13
(
a
9
a
1
a
1
+
a
1
a
9
a
1
+
a
1
a
1
a
9
+
a
5
a
5
a
1
+
a
5
a
1
a
5
+
a
1
a
5
a
5
)
=
−
11
15600
.
{\displaystyle {\begin{aligned}a_{13}&=-{\tfrac {2}{12\cdot 13}}(a_{9}a_{1}a_{1}+a_{1}a_{9}a_{1}+a_{1}a_{1}a_{9}+a_{5}a_{5}a_{1}+a_{5}a_{1}a_{5}+a_{1}a_{5}a_{5})=-{\tfrac {11}{15600}}.\end{aligned}}}
Зв'язок з еліптичними функціями Веєрштрасса і Якобі [ ред. | ред. код ] Лемніскатні функції тісно пов'язані з еліптичними функціями Веєрштрасса
℘
(
z
;
1
,
0
)
{\displaystyle \wp (z;1,0)}
g
2
=
1
{\displaystyle g_{2}=1}
g
3
=
0
{\displaystyle g_{3}=0}
ω
1
=
2
ϖ
{\displaystyle \omega _{1}={\sqrt {2}}\varpi }
ω
2
=
i
ω
1
{\displaystyle \omega _{2}={\rm {i}}\omega _{1}}
e
1
=
1
2
{\displaystyle e_{1}={\tfrac {1}{2}}}
e
2
=
0
{\displaystyle e_{2}=0}
e
3
=
−
1
2
{\displaystyle e_{3}=-{\tfrac {1}{2}}}
Пов'язаний випадок еліптичної функції Веєрштрасса з інваріантами
g
2
=
a
{\displaystyle g_{2}=a}
g
3
=
0
{\displaystyle g_{3}=0}
a
>
0
{\displaystyle a>0}
a
<
0
{\displaystyle a<0}
паралелограм є квадратом або ромбом .
Еліптичну функцію Вейєрштрасса
℘
(
z
;
−
1
,
0
)
{\displaystyle \wp (z;-1,0)}
[44]
Квадрат лемніскати синуса можна представити як
sl
2
z
=
1
℘
(
z
;
4
,
0
)
=
i
2
℘
(
(
1
−
i
)
z
;
−
1
,
0
)
=
−
2
℘
(
2
z
+
(
i
−
1
)
ϖ
2
;
1
,
0
)
,
{\displaystyle {\begin{aligned}\operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {\rm {i}}{2\wp ((1-{\rm {i}})z;-1,0)}}=-2\wp \left({\sqrt {2}}z+({\rm {i}}-1){\frac {\varpi }{\sqrt {2}}};1,0\right),\end{aligned}}}
де другий і третій аргументи еліптичної функції Веєрштрасса
℘
{\displaystyle \wp }
g
2
{\displaystyle g_{2}}
g
3
{\displaystyle g_{3}}
sl
2
z
=
ϖ
2
℘
(
z
/
ϖ
,
i
)
,
{\displaystyle {\begin{aligned}\operatorname {sl} ^{2}z={\frac {\varpi ^{2}}{\wp (z/\varpi ,{\rm {i}})}},\end{aligned}}}
де другий аргумент еліптичної функції Веєрштрасса
℘
{\displaystyle \wp }
τ
{\displaystyle \tau }
[45] раціональною функцією еліптичної функції Веєрштрасса та її похідної[46]
sl
z
=
−
2
℘
(
(
1
+
i
)
z
;
1
/
4
,
0
)
℘
′
(
(
1
+
i
)
z
;
1
/
4
,
0
)
,
{\displaystyle {\begin{aligned}\operatorname {sl} z=-2{\frac {\wp ((1+{\rm {i}})z;1/4,0)}{\wp '((1+{\rm {i}})z;1/4,0)}},\end{aligned}}}
де другий і третій аргументи еліптичної функції Веєрштрасса
℘
{\displaystyle \wp }
g
2
{\displaystyle g_{2}}
g
3
{\displaystyle g_{3}}
τ
{\displaystyle \tau }
sl
z
=
−
2
℘
(
(
1
+
i
)
z
/
(
2
ϖ
)
,
i
)
℘
′
(
(
1
+
i
)
z
/
(
2
ϖ
)
,
i
)
.
{\displaystyle {\begin{aligned}\operatorname {sl} z=-2{\frac {\wp ((1+{\rm {i}})z/(2\varpi ),{\rm {i}})}{\wp '((1+{\rm {i}})z/(2\varpi ),{\rm {i}})}}.\end{aligned}}}
Лемніскатні функції також можуть бути записані в термінах еліптичних функцій Якобі .
Еліптичні функції Якобі
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
i
{\displaystyle {\rm {i}}}
sd
{\displaystyle \operatorname {sd} }
cn
{\displaystyle \operatorname {cn} }
1
/
2
{\displaystyle 1/{\sqrt {2}}}
[47]
sl
z
=
sn
(
z
;
i
)
=
1
2
sd
(
2
z
;
1
2
)
,
cl
z
=
cd
(
z
;
i
)
=
cn
(
2
z
;
1
2
)
,
{\displaystyle {\begin{aligned}&\operatorname {sl} z=\operatorname {sn} (z;{\rm {i}})={\tfrac {1}{\sqrt {2}}}\operatorname {sd} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),\\&\operatorname {cl} z=\operatorname {cd} (z;{\rm {i}})=\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),\end{aligned}}}
де другі аргументи — еліптичний модуль
k
{\displaystyle k}
Ще одне представлення лемніскатної функції
cl
{\displaystyle \operatorname {cl} }
dn
{\displaystyle \operatorname {dn} }
cl
z
=
dn
(
z
;
2
)
,
{\displaystyle {\begin{aligned}\operatorname {cl} z=\operatorname {dn} (z;{\sqrt {2}}),\end{aligned}}}
де другий аргумент еліптичної функції Якобі
dn
{\displaystyle \operatorname {dn} }
k
{\displaystyle k}
Зв'язок з модулярною лямбда-функцією [ ред. | ред. код ] Лемніскатну функцію синуса можна використовувати для обчислення значень модулярної лямбда-функції :
∏
k
=
1
n
sl
(
2
k
−
1
2
n
+
1
ϖ
2
)
=
λ
(
(
2
n
+
1
)
i
)
1
−
λ
(
(
2
n
+
1
)
i
)
8
.
{\displaystyle {\begin{aligned}\prod _{k=1}^{n}\operatorname {sl} \left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)={\sqrt[{8}]{\frac {\lambda ((2n+1){\rm {i}})}{1-\lambda ((2n+1){\rm {i}})}}}.\end{aligned}}}
Наприклад,
sl
(
1
14
ϖ
)
,
sl
(
3
14
ϖ
)
sl
(
5
14
ϖ
)
=
λ
(
7
i
)
1
−
λ
(
7
i
)
8
=
tg
(
1
2
arccsc
(
1
2
8
7
+
21
+
1
2
7
+
1
)
)
,
sl
(
1
18
ϖ
)
,
sl
(
3
18
ϖ
)
,
sl
(
5
18
ϖ
)
,
sl
(
7
18
ϖ
)
=
λ
(
9
i
)
1
−
λ
(
9
i
)
8
=
tg
(
π
4
−
arctg
(
2
2
3
−
2
3
−
2
2
−
3
3
+
3
−
1
12
4
)
)
.
{\displaystyle {\begin{aligned}&\operatorname {sl} {\bigl (}{\tfrac {1}{14}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\operatorname {sl} {\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}={\sqrt[{8}]{\frac {\lambda (7{\rm {i}})}{1-\lambda (7{\rm {i}})}}}=\operatorname {tg} {\Bigl (}{\tfrac {1}{2}}\operatorname {arccsc} {\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )},\\&\operatorname {sl} {\bigl (}{\tfrac {1}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {3}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {5}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}={\sqrt[{8}]{\frac {\lambda (9{\rm {i}})}{1-\lambda (9{\rm {i}})}}}=\operatorname {tg} {\Biggl (}{\frac {\pi }{4}}-\operatorname {arctg} {\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}.\end{aligned}}}
Декілька методів обчислення функції
sl
x
{\displaystyle \operatorname {sl} x}
π
x
=
ϖ
x
~
{\displaystyle \pi x=\varpi {\tilde {x}}}
sl
(
ϖ
x
~
/
π
)
{\displaystyle \operatorname {sl} (\varpi {\tilde {x}}/\pi )}
Метод гіперболічних рядів :[50] [51] [52] [53]
sl
(
ϖ
π
x
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
ch
(
x
−
(
n
+
1
/
2
)
π
)
,
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sh
(
x
−
n
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sin
(
x
−
n
π
i
)
.
{\displaystyle {\begin{aligned}&\operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\operatorname {ch} (x-(n+1/2)\pi )}},\\&{\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\operatorname {sh} \left(x-n\pi \right)}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\sin(x-n\pi {\rm {i}})}}.\end{aligned}}}
Метод рядів Фур'є :[54]
sl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
(
−
1
)
n
sin
(
(
2
n
+
1
)
x
)
ch
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
,
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
(
1
sin
x
−
4
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
e
(
2
n
+
1
)
π
+
1
)
,
|
Im
x
|
<
π
.
{\displaystyle {\begin{aligned}&\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {(-1)^{n}\sin((2n+1)x)}{\operatorname {ch} ((n+1/2)\pi )}},\ \left|\operatorname {Im} x\right|<{\frac {\pi }{2}},\\&{\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\left({\frac {1}{\sin x}}-4\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{{\rm {e}}^{(2n+1)\pi }+1}}\right),\ \left|\operatorname {Im} x\right|<\pi .\end{aligned}}}
Лемніскатні функції можуть бути обчислені більш швидше за допомогою формул
sl
(
ϖ
π
x
)
=
θ
1
(
x
,
e
−
π
)
θ
3
(
x
,
e
−
π
)
,
cl
(
ϖ
π
x
)
=
θ
2
(
x
,
e
−
π
)
θ
4
(
x
,
e
−
π
)
,
{\displaystyle {\begin{aligned}&\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {\theta _{1}\left(x,{\rm {e}}^{-\pi }\right)}{\theta _{3}\left(x,{\rm {e}}^{-\pi }\right)}},\\&\operatorname {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {\theta _{2}\left(x,{\rm {e}}^{-\pi }\right)}{\theta _{4}\left(x,{\rm {e}}^{-\pi }\right)}},\end{aligned}}}
де
θ
1
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
+
1
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
1
/
2
)
2
sin
(
(
2
n
+
1
)
x
)
,
θ
2
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
)
2
cos
(
(
2
n
+
1
)
x
)
,
θ
3
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
n
2
cos
2
n
x
,
θ
4
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
n
2
cos
2
n
x
{\displaystyle {\begin{aligned}&\theta _{1}(x,{\rm {e}}^{-\pi })=\sum _{n\in \mathbb {Z} }(-1)^{n+1}{\rm {e}}^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}{\rm {e}}^{-\pi (n+1/2)^{2}}\sin((2n+1)x),\\&\theta _{2}(x,{\rm {e}}^{-\pi })=\sum _{n\in \mathbb {Z} }(-1)^{n}{\rm {e}}^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }{\rm {e}}^{-\pi (n+1/2)^{2}}\cos((2n+1)x),\\&\theta _{3}(x,{\rm {e}}^{-\pi })=\sum _{n\in \mathbb {Z} }{\rm {e}}^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }{\rm {e}}^{-\pi n^{2}}\cos 2nx,\\&\theta _{4}(x,{\rm {e}}^{-\pi })=\sum _{n\in \mathbb {Z} }{\rm {e}}^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}{\rm {e}}^{-\pi n^{2}}\cos 2nx&\end{aligned}}}
— тета-функції Якобі .[55]
Два інші методи швидкого обчислення використовують наступні формули сум і добутків рядів:
sl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
sin
x
∑
n
=
1
∞
ch
[
(
2
n
−
1
)
π
]
ch
2
[
(
2
n
−
1
)
π
]
−
cos
2
x
)
,
cl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
cos
x
∑
n
=
1
∞
ch
[
(
2
n
−
1
)
π
]
ch
2
[
(
2
n
−
1
)
π
]
−
sin
2
x
)
,
sl
(
ϖ
π
x
)
=
2
e
−
π
/
4
sin
x
∏
n
=
1
∞
1
−
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
+
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
cl
(
ϖ
π
x
)
=
2
e
−
π
/
4
cos
x
∏
n
=
1
∞
1
+
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
−
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
{\displaystyle {\begin{aligned}&\operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=f\left({\frac {4\pi }{\varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\operatorname {ch} [(2n-1)\pi ]}{\operatorname {ch} ^{2}[(2n-1)\pi ]-\cos ^{2}x}}\right),\\&\operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)=f\left({\frac {4\pi }{\varpi }}\cos x\sum _{n=1}^{\infty }{\frac {\operatorname {ch} [(2n-1)\pi ]}{\operatorname {ch} ^{2}[(2n-1)\pi ]-\sin ^{2}x}}\right),\\&\operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=2{\rm {e}}^{-\pi /4}\sin x\prod _{n=1}^{\infty }{\frac {1-2{\rm {e}}^{-2n\pi }\cos 2x+{\rm {e}}^{-4n\pi }}{1+2{\rm {e}}^{-(2n-1)\pi }\cos 2x+{\rm {e}}^{-(4n-2)\pi }}},\\&\operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)=2{\rm {e}}^{-\pi /4}\cos x\prod _{n=1}^{\infty }{\frac {1+2{\rm {e}}^{-2n\pi }\cos 2x+{\rm {e}}^{-4n\pi }}{1-2{\rm {e}}^{-(2n-1)\pi }\cos 2x+{\rm {e}}^{-(4n-2)\pi }}},\end{aligned}}}
де
f
(
x
)
=
tg
(
2
arctg
x
)
=
2
x
/
(
1
−
x
2
)
{\displaystyle f(x)=\operatorname {tg} (2\operatorname {arctg} x)=2x/(1-x^{2})}
Ряд Фур'є для логарифма лемнікатного синуса має вигляд:
ln
sl
(
ϖ
π
x
)
=
ln
2
−
π
4
+
ln
sin
x
+
2
∑
n
=
1
∞
(
−
1
)
n
cos
2
n
x
n
(
e
n
π
+
(
−
1
)
n
)
,
|
Im
x
|
<
π
2
.
{\displaystyle {\begin{aligned}\ln \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=\ln 2-{\frac {\pi }{4}}+\ln \sin x+2\sum _{n=1}^{\infty }{\frac {(-1)^{n}\cos 2nx}{n({\rm {e}}^{n\pi }+(-1)^{n})}},\ \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}.\end{aligned}}}
Рамануджан відкрив наступні співвідношення для рядів:[56]
ϖ
2
π
2
sl
2
(
ϖ
x
/
π
)
=
1
sin
2
x
−
1
π
−
8
∑
n
=
1
∞
n
cos
2
n
x
e
2
n
π
−
1
,
|
Im
x
|
<
π
,
arctg
sl
(
ϖ
π
x
)
=
2
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
(
2
n
+
1
)
ch
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
.
{\displaystyle {\begin{aligned}&{\frac {\varpi ^{2}}{\pi ^{2}\operatorname {sl} ^{2}(\varpi x/\pi )}}={\frac {1}{\sin ^{2}x}}-{\frac {1}{\pi }}-8\sum _{n=1}^{\infty }{\frac {n\cos 2nx}{{\rm {e}}^{2n\pi }-1}},\quad \left|\operatorname {Im} x\right|<\pi ,\\&\operatorname {arctg} \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=2\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{(2n+1)\operatorname {ch} ((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}.\end{aligned}}}
Оберненою функцією для лемніскатного синуса є лемніскатний арксинус визначений як:
arcsl
x
=
∫
0
x
d
t
1
−
t
4
.
{\displaystyle {\begin{aligned}\operatorname {arcsl} x=\int _{0}^{x}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}.\end{aligned}}}
Її також можна представити за допомогою гіпергеометричної функції :
arcsl
x
=
x
2
F
1
(
1
2
,
1
4
;
5
4
;
x
4
)
.
{\displaystyle {\begin{aligned}\operatorname {arcsl} x={x}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{4}};{\tfrac {5}{4}};x^{4}\right).\end{aligned}}}
Оберненою функцією для лемніскатного косинуса є лемніскатний арккосинус.
Ця функція визначається наступним чином:
arccl
x
=
∫
x
1
d
t
1
−
t
4
=
1
2
ϖ
−
arcsl
x
.
{\displaystyle {\begin{aligned}\operatorname {arccl} x=\int _{x}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}={\tfrac {1}{2}}\varpi -\operatorname {arcsl} x.\end{aligned}}}
Для
x
{\displaystyle x}
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
sl
(
arcsl
x
)
=
x
{\displaystyle \operatorname {sl} (\operatorname {arcsl} x)=x}
cl
(
arccl
x
)
=
x
{\displaystyle \operatorname {cl} (\operatorname {arccl} x)=x}
Для половини довжини лемніскатної дуги справедливі формули:
sl
(
1
2
arcsl
x
)
=
sin
(
1
2
arcsin
x
)
sech
(
1
2
arsinh
x
)
,
sl
(
1
2
arcsl
x
)
2
=
tg
(
1
4
arcsin
x
2
)
.
{\displaystyle {\begin{aligned}&\operatorname {sl} {\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}=\sin {\bigl (}{\tfrac {1}{2}}\arcsin x{\bigr )}\operatorname {sech} {\bigl (}{\tfrac {1}{2}}\operatorname {arsinh} x{\bigr )},\\&\operatorname {sl} {\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}^{2}=\operatorname {tg} {\bigl (}{\tfrac {1}{4}}\arcsin x^{2}{\bigr )}.\end{aligned}}}
Співвідношення з використанням еліптичних інтегралів [ ред. | ред. код ] Лемініскатний арксинус і лемніскатний арккосинус також можна представити за допомогою форми Лежандра.
Ці функції можна представити безпосередньо, використовуючи неповний еліптичний інтеграл першого роду:
arcsl
x
=
1
2
F
(
arcsin
2
x
1
+
x
2
;
1
2
)
,
arcsl
x
=
2
(
2
−
1
)
F
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
.
{\displaystyle {\begin{aligned}&\operatorname {arcsl} x={\frac {1}{\sqrt {2}}}F\left(\arcsin {\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right),\\&\operatorname {arcsl} x=2{\big (}{\sqrt {2}}-1{\big )}F\left(\arcsin {\frac {{\big (}{\sqrt {2}}+1{\big )}x}{{\sqrt {1+x^{2}}}+1}};{\big (}{\sqrt {2}}-1{\big )}^{2}\right).\end{aligned}}}
Довжини дуг лемніскати також можна виразити лише за допомогою довжин дуг еліпсів (обчислених за допомогою еліптичних інтегралів другого роду):
arcsl
x
=
2
+
2
2
E
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
−
E
(
arcsin
2
x
1
+
x
2
;
1
2
)
+
x
1
−
x
2
2
(
1
+
x
2
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}
Лемніскатний арккосинус має наступне співвідношення:
arccl
x
=
1
2
F
(
arccos
x
;
1
2
)
.
{\displaystyle {\begin{aligned}\operatorname {arccl} x={\tfrac {1}{\sqrt {2}}}F\left(\arccos x;{\tfrac {1}{\sqrt {2}}}\right).\end{aligned}}}
Використання при інтегруванні [ ред. | ред. код ] Лемніскатну функцію можна використовувати для інтегрування багатьох функцій.
Ось список важливих інтегралів (константи інтегрування опущені):
∫
1
1
−
x
4
d
x
=
arcsl
x
,
∫
1
(
x
2
+
1
)
(
2
x
2
+
1
)
d
x
=
arcsl
x
x
2
+
1
,
∫
1
x
4
+
6
x
2
+
1
d
x
=
arcsl
2
x
x
4
+
6
x
2
+
1
+
x
2
+
1
,
∫
1
x
4
+
1
d
x
=
2
arcsl
x
x
4
+
1
+
1
,
∫
1
(
1
−
x
4
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
4
,
∫
1
(
x
4
+
1
)
3
4
d
x
=
arcsl
x
x
4
+
1
4
,
∫
1
(
1
−
x
2
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
2
,
∫
1
(
x
2
+
1
)
3
4
d
x
=
2
arcsl
x
x
2
+
1
+
1
,
∫
1
(
a
x
2
+
b
x
+
c
)
3
4
d
x
=
2
2
4
a
2
c
−
a
b
2
4
arcsl
2
a
x
+
b
4
a
(
a
x
2
+
b
x
+
c
)
+
4
a
c
−
b
2
,
∫
sech
x
d
x
=
2
arcsl
(
th
1
2
x
)
,
∫
sec
x
d
x
=
2
arcsl
(
tg
1
2
x
)
.
{\displaystyle {\begin{aligned}&\int {\frac {1}{\sqrt {1-x^{4}}}}{\rm {d}}x=\operatorname {arcsl} x,\\&\int {\frac {1}{\sqrt {{\big (}x^{2}+1{\big )}{\big (}2x^{2}+1{\big )}}}}{\rm {d}}x=\operatorname {arcsl} {\frac {x}{\sqrt {x^{2}+1}}},\\&\int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}{\rm {d}}x=\operatorname {arcsl} {\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}},\\&\int {\frac {1}{\sqrt {x^{4}+1}}}{\rm {d}}x={\sqrt {2}}\operatorname {arcsl} {\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}1-x^{4}{\big )}^{3}}}}{\rm {d}}x={\sqrt {2}}\operatorname {arcsl} {\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}x^{4}+1{\big )}^{3}}}}{\rm {d}}x=\operatorname {arcsl} {\frac {x}{\sqrt[{4}]{x^{4}+1}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}1-x^{2}{\big )}^{3}}}}{\rm {d}}x=2\operatorname {arcsl} {\frac {x}{1+{\sqrt {1-x^{2}}}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}x^{2}+1{\big )}^{3}}}}{\rm {d}}x=2\operatorname {arcsl} {\frac {x}{{\sqrt {x^{2}+1}}+1}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}ax^{2}+bx+c{\big )}^{3}}}}{\rm {d}}x={\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} {\frac {2ax+b}{{\sqrt {4a{\big (}ax^{2}+bx+c{\big )}}}+{\sqrt {4ac-b^{2}}}}},\\&\int {\sqrt {\operatorname {sech} x}}{\rm {d}}x=2\operatorname {arcsl} {\big (}\operatorname {th} {\tfrac {1}{2}}x{\big )},\\&\int {\sqrt {\sec x}}{\rm {d}}x=2\operatorname {arcsl} {\big (}\operatorname {tg} {\tfrac {1}{2}}x{\big )}.\end{aligned}}}
Гіперболічні лемніскатні функції [ ред. | ред. код ] Функції гіперболічний лемніскатний синус (червоні лінії) і гіперболічний лемніскатний косинус (пурпурові лінії) дійсного аргументу в порівнянні з тригонометричним тангенсом (шриховані блідо-червоні лінії). Гіперболічну лемніскату синуса
(
slh
)
{\displaystyle (\operatorname {slh} )}
(
clh
)
{\displaystyle (\operatorname {clh} )}
z
=
∫
0
slh
z
d
t
1
+
t
4
=
∫
clh
z
∞
d
t
1
+
t
4
.
{\displaystyle {\begin{aligned}z=\int _{0}^{\operatorname {slh} z}{\frac {{\rm {d}}t}{\sqrt {1+t^{4}}}}=\int _{\operatorname {clh} z}^{\infty }{\frac {{\rm {d}}t}{\sqrt {1+t^{4}}}}.\end{aligned}}}
Повний інтеграл набуває значення:
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
1
2
ϖ
=
1,854
07
46773
01371
…
.
{\displaystyle {\begin{aligned}\int _{0}^{\infty }{\frac {{\rm {d}}t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}{\rm {B}}{\big (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\big )}={\tfrac {1}{\sqrt {2}}}\varpi =1{,}85407\;46773\;01371\dots .\end{aligned}}}
Тому дві визначені функції допускають наступне співвідношення:
slh
z
=
clh
(
1
2
ϖ
−
z
)
.
{\displaystyle {\begin{aligned}\operatorname {slh} z=\operatorname {clh} {\bigl (}{\tfrac {1}{\sqrt {2}}}\varpi -z{\bigr )}.\end{aligned}}}
Добуток гіперболічного лемніскатного синуса і гіперболічного лемніскатного косинуса дорівнює одиниці:
slh
z
clh
z
=
1.
{\displaystyle {\begin{aligned}\operatorname {slh} z\,\operatorname {clh} z=1.\end{aligned}}}
Гіперболічні лемніскатні функції можуть бути представлені через лемніскатний синус і лемніскатний косинус:
slh
(
2
x
)
=
(
1
+
cl
2
x
)
sl
x
2
cl
x
,
clh
(
2
x
)
=
(
1
+
sl
2
x
)
cl
x
2
sl
x
.
{\displaystyle {\begin{aligned}&\operatorname {slh} {\bigl (}{\sqrt {2}}x{\bigr )}={\frac {{\big (}1+\operatorname {cl} ^{2}x{\big )}\operatorname {sl} x}{{\sqrt {2}}\operatorname {cl} x}},\\&\operatorname {clh} {\bigl (}{\sqrt {2}}x{\bigr )}={\frac {{\big (}1+\operatorname {sl} ^{2}x{\big )}\operatorname {cl} x}{{\sqrt {2}}\operatorname {sl} x}}.\end{aligned}}}
Але також існує зв'язок із еліптичними функціямі Якобі з еліптичним модулем
1
/
2
{\displaystyle 1/{\sqrt {2}}}
slh
x
=
sn
(
x
;
1
/
2
)
cd
(
x
;
1
/
2
)
,
clh
x
=
cd
(
x
;
1
/
2
)
sn
(
x
;
1
/
2
)
.
{\displaystyle {\begin{aligned}\operatorname {slh} x={\frac {\operatorname {sn} {\big (}x;1/{\sqrt {2}}{\big )}}{\operatorname {cd} {\big (}x;1/{\sqrt {2}}{\big )}}},\\\operatorname {clh} x={\frac {\operatorname {cd} {\big (}x;1/{\sqrt {2}}{\big )}}{\operatorname {sn} {\big (}x;1/{\sqrt {2}}{\big )}}}.\end{aligned}}}
Гіперболічний лемніскатний синус допускає наступне уявне співвідношення із лемніскатним синусом:
slh
z
=
1
−
i
2
sl
(
1
+
i
2
z
)
=
sl
(
−
1
4
z
)
−
1
4
.
{\displaystyle {\begin{aligned}\operatorname {slh} z={\frac {1-{\rm {i}}}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+{\rm {i}}}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}.\end{aligned}}}
Аналогічний зв'язок існує і між гіперболічним і тригонометричним синусом:
sinh
z
=
−
i
sin
(
i
z
)
=
sin
(
−
1
2
z
)
−
1
2
.
{\displaystyle {\begin{aligned}\operatorname {sinh} z=-{\rm {i}}\sin({\rm {i}}z)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}.\end{aligned}}}
Відносно кривої Ферма четвертого порядку
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
Крива Ферма
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
квадратним колом [en]
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
L
{\displaystyle L}
x
{\displaystyle x}
y
{\displaystyle y}
L
{\displaystyle L}
x
=
1
{\displaystyle x=1}
[57]
Гіперболічний лемніскатний синус задовольняє тотожність додавання аргументів:
slh
(
a
+
b
)
=
slh
a
1
+
slh
4
b
+
slh
b
1
+
slh
4
a
1
−
slh
2
a
slh
2
b
.
{\displaystyle {\begin{aligned}\operatorname {slh} (a+b)={\frac {\operatorname {slh} a{\sqrt {1+\operatorname {slh} ^{4}b}}+\operatorname {slh} b{\sqrt {1+\operatorname {slh} ^{4}a}}}{1-\operatorname {slh} ^{2}a\operatorname {slh} ^{2}b}}.\end{aligned}}}
Похідна може бути виражена наступним чином:
d
d
x
slh
x
=
1
+
slh
4
x
.
{\displaystyle {\begin{aligned}{\frac {\rm {d}}{{\rm {d}}x}}\operatorname {slh} x={\sqrt {1+\operatorname {slh} ^{4}x}}.\end{aligned}}}
В алгебричній теорії чисел , будь-яке скінченне абелеве розширення гаусових раціональних чисел [en]
Q
(
i
)
{\displaystyle {\rm {Q}}({\rm {i}})}
підполем поля
Q
(
i
,
sl
(
2
ϖ
/
n
)
)
{\displaystyle {\rm {Q}}({\rm {i}},\operatorname {sl} (2\varpi /n))}
n
{\displaystyle n}
[58] [59] теореми Кронекера-Вебера для раціональних чисел
Q
{\displaystyle {\rm {Q}}}
Q
{\displaystyle {\rm {Q}}}
Q
(
exp
(
2
π
i
/
n
)
)
{\displaystyle {\rm {Q}}(\exp(2\pi {\rm {i}}/n))}
n
{\displaystyle n}
дванадцята проблема Гільберта [en]
Поле
Q
(
i
,
sl
(
ϖ
/
n
)
)
{\displaystyle {\rm {Q}}({\rm {i}},\operatorname {sl} (\varpi /n))}
n
{\displaystyle n}
Q
(
i
)
{\displaystyle {\rm {Q}}({\rm {i}})}
x
{\displaystyle x}
y
{\displaystyle y}
(
1
+
i
)
n
{\displaystyle (1+{\rm {i}})n}
скруту на еліптичній кривій
y
2
=
4
x
3
+
x
{\displaystyle y^{2}=4x^{3}+x}
[60]
Проєкція карти світу [ ред. | ред. код ] «Світ при квінкунціальній проєкції», Чарлз Сандерс Пірс (1879). Квінкунціальна проєкція Пірса [en] Чарльзом Сандерсом Пірсом із Національної геодезичної служби США [en] проєкцією карти світу , що базується на оберненій лемніскаті синуса стереграфічно спроєктованих точок (що розглядаються як комплексні числа).[61]
Якщо прямі постійної дійсної або уявної частини проєктувати на комплексну площину за допомогою гіперболічного лемніскатного синусу, а звідки їх стереографічно проєктувати на сферу (див. Сферу Рімана ), то отримані криві є сферичними коніками [en] [62] еліптичні функції Якобі ) забезпечують параметризацію для сферичних конік.
Конформну картографічну проєкцію земної кулі на 6 квадратних граней куба також можна визначити за допомогою лемніскатних функцій.[63] диференціальних рівнянь з частинними похідними можна ефективно розв'язати за допомогою конформного відображення, то перетворення сфери в куб зручне для моделювання атмосфери [en] [64]
↑ Гаус використовував символи
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
sine
{\displaystyle \operatorname {sine} }
cosine
{\displaystyle \operatorname {cosine} }
sinlemn
{\displaystyle \operatorname {sinlemn} }
coslemn
{\displaystyle \operatorname {coslemn} }
s
{\displaystyle \operatorname {s} }
c
{\displaystyle \operatorname {c} }
ϕ
{\displaystyle \phi }
sine
{\displaystyle \operatorname {sine} }
ϕ
′
{\displaystyle \phi '}
↑ Фундаментальні періоди
(
1
+
i
)
ϖ
{\displaystyle (1+{\rm {i}})\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-{\rm {i}})\varpi }
↑ Робінсон (2019a) стартував з цього означення і далі отримував інші властивості лемніскатних функцій.
↑ Це відображення було першою ілюстрацією для відображення Шварца—Крістофелля, див. Шварц (1869).
↑ Ейлер (1761), Сігел, (1969), Прасолов і Соловйов (1997) для лемніскати використовували представлення у полярних координатах, щоб визначити диференціал довжини дуги кривої, але результат буде той же.
↑ Siegel (1969), Schappacher (1997).
↑ Числа A003401 в OEIS.
↑ Abel (1827—1828), Rosen (1981), Prasolov & Solovyev (1997).
↑ Euler (1786), Sridharan (2004), Levien (2008).
↑ Темні області представляють нулі, а яскраві області — полюси. Оскільки аргумент функції
sl
z
{\displaystyle \operatorname {sl} z}
−
π
{\displaystyle -\pi }
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
ARG
≈
0
)
{\displaystyle (\operatorname {ARG} \approx 0)}
(
ARG
≈
π
/
2
)
{\displaystyle (\operatorname {ARG} \approx \pi /2)}
(
ARG
≈
π
)
{\displaystyle (\operatorname {ARG} \approx \pi )}
↑ Schappacher (1997). Послідовність OEIS A062539 містить десяткові цифри лемніскатної константи.
↑ Як правило константа
ϖ
{\displaystyle \varpi }
↑ Архівована копія . Архів оригіналу за 30 січня 2022. Процитовано 23 травня 2022 .{{cite web }}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання )↑ «Lemniscate Constant».
↑ а б Todd (1975).
↑ «A085565 — Oeis».
↑ Carlson, B. C. (2010), «Elliptic Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248.
↑ Schneider (1937).
↑ G.V.Choodnovsky: Algebraic independence of constants connected with the functions of analysis, Notices of the AMS 22, 1975, p.A-486.
↑ G.V.Chudnovsky: Contributions to The Theory of Transcendental Numbers, American Mathematical Society, 1984, p.6.
↑ Левін (2008). Тод (1975) називав ці два множники
A
=
ϖ
/
2
{\displaystyle A=\varpi /2}
B
=
π
/
2
ϖ
{\displaystyle B=\pi /2\varpi }
↑ Левін (2006).
↑ Хайд у 2014 довів справедливість більш загальної формули типу Валіса для кривих конюшини; тут спеціальний випадок лемніскати трохи модифіковано для наочності.
↑ Bottazzini Gray (2013), p.60.
↑ Cox, David (January 1984). «The Arithmetic-Geometric Mean of Gauss». L'Enseignement Matematique. 30(2): 275—330. See p.307, eq.2.21 для першої рівності.
↑ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (французькою). HERMANN. ISBN 2705614435 . p.224.
↑ Комбінація першої і четвертої тотожності дає
sl
z
=
−
i
/
sl
(
z
−
(
1
+
i
)
ϖ
/
2
)
{\displaystyle \operatorname {sl} z=-{\rm {i}}/\operatorname {sl} (z-(1+{\rm {i}})\varpi /2)}
↑ Цілі числа Гаусса — це клас лишків 0 за модулем
1
+
i
{\displaystyle 1+{\rm {i}}}
↑ Prasolov Solovyev (1997), Robinson (2019a).
↑ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (in French). HERMANN. ISBN 2705614435 . p.218.
↑ Bottazzini, Umberto; Gray, Jeremy (2013). Hidden Harmony—Geometric Fantasies. Springer. ISBN 978-1-4614-5724-4 . p.58
↑ Гаусс записав добутки для
M
{\displaystyle M}
N
{\displaystyle N}
M
{\displaystyle M}
N
{\displaystyle N}
N
(
2
z
)
=
M
4
(
z
)
+
N
4
(
z
)
{\displaystyle N(2z)=M^{4}(z)+N^{4}(z)}
↑ а б Reinhardt, W. P.; Walker, P. L. (2010), «Jacobian Elliptic Functions», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
↑ Аналогічно,
1
sin
z
=
∑
n
∈
Z
(
−
1
)
n
z
+
n
π
{\displaystyle \displaystyle {\frac {1}{\sin z}}=\sum \limits _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{z+n\pi }}}
↑ Lindqvist Peetre (2001) узагальнює першу з цих форм.
↑ Ayoub (1984), Prasolov Solovyev (1997).
↑ Euler (1761), § 44 p. 79 , § 47 pp. 80–81
↑ а б Euler (1761) § 46 p. 80
↑ Фактично,
i
ε
=
sl
β
ϖ
2
{\displaystyle {\rm {i}}^{\varepsilon }=\operatorname {sl} {\tfrac {\beta \varpi }{2}}}
↑ а б Cox and Hyde (2014).
↑ Gómez-Molleda, M. A.; Lario, Joan-C. (25 квітня 2019). Ruler and Compass Constructions of the Equilateral Triangle and Pentagon in the Lemniscate Curve . The Mathematical Intelligencer . 41 (4): 17—21. doi :10.1007/s00283-019-09892-w . S2CID 149727564 . Архів оригіналу за 23 березня 2022. Процитовано 26 травня 2022 . ↑ Rosen (1981).
↑ «A104203». The On-Line Encyclopedia of Integer Sequences.
↑ Robinson (2019a).
↑
℘
(
z
,
τ
)
{\displaystyle \wp (z,\tau )}
ω
2
/
ω
1
=
τ
{\displaystyle \omega _{2}/\omega _{1}=\tau }
↑ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (in French). HERMANN. ISBN2705614435. p.226.
↑ Тотожність
cl
z
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z=\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
↑ Reinhardt Walker (2010), 22.20.
↑ Carlson (2010), §19.8
↑ Dieckmann, Andreas. "Collection of Infinite Products and Series".
↑ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248.
↑ Vigren Dieckmann (2020), p.7.
↑ У загальному випадку
sh
(
x
−
n
π
)
{\displaystyle \operatorname {sh} (x-n\pi )}
sin
(
x
−
n
π
i
)
=
−
i
sh
(
i
x
+
n
π
)
{\displaystyle \sin(x-n\pi {\rm {i}})=-{\rm {i}}\operatorname {sh} ({\rm {i}}x+n\pi )}
↑ Reinhardt Walker (2010), 22.11.
↑ Reinhardt Walker (2010), 22.2.E7
↑ Berndt, Bruce C. (1994). Ramanujan's Notebooks Part IV (First ed.). Springer Science+Business Media New York. ISBN 978-1-4612-6932-8 . p.247,248,253.
↑ Levin (2006), Robinson (2019b)
↑ Cox and Hyde (2014)
↑ Cox, David A. (2012). Galois Theory (Second ed.). Wiley. ISBN 978-1-118-07205-9 . p. 508,509
↑ Cox, David A. (2012). Galois Theory (Second ed.). Wiley. ISBN 978-1-118-07205-9 . p.508-509.
↑ Гут (1887) і Адамс (1925) ввели відповідно поперечні і скісні аспекти тієї ж проєкції, відповідно. Також дивись Лі (1976). Ці автори записали свої проєкційні формули в термінах еліптичних функцій Якобі з квадратною ґраткою.
↑ Adams (1925)
↑ Adams (1925), Lee (1976).
↑ Rančić, Purser, Mesinger (1996); McGregor (2005).
Abel, Niels Henrik (1827–1828). [113 } Recherches sur les fonctions elliptiques] [Research on elliptical functions]. Crelle's Journal (фр.) . 1827 (2): 101—181. doi :10.1515/crll.1827.2.101 . S2CID 126159170 .[166 } Recherches sur les fonctions elliptiques]. Crelle's Journal . 1828 (3): 160—190. doi :10.1515/crll.1828.3.160 . S2CID 123647093 .Adams, Oscar Sherman (1925). Elliptic functions applied to conformal world maps (PDF) . № 297. US Government Printing Office. Ayoub, Raymond (1984). The Lemniscate and Fagnano's Contributions to Elliptic Integrals . Archive for History of Exact Sciences . 29 (2): 131—149. JSTOR 41133708 . Bottazzini, Umberto; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 Carlson, Billie C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; et al. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Cox, David Archibald (2012). The Lemniscate. Galois Theory 463 –514. doi :10.1002/9781118218457.ch15 . ISBN 978-1-118-21845-7 Cox, David Archibald; Hyde, Trevor (2014). The Galois theory of the lemniscate (PDF) . Journal of Number Theory . 135 : 43—59. arXiv :1208.2653 doi :10.1016/j.jnt.2013.08.006 . S2CID 119176369 . Enneper, Alfred (1890 ed. 1876). Note III: Historische Notizen über geometrische Anwendungen elliptischer Integrale. [Historical notes on geometric applications of elliptic integrals]. Elliptische Functionen, Theorie und Geschichte (нім.) . Nebert. с. 524—547. Euler, Leonhard (1761). Observationes de comparatione arcuum curvarum irrectificibilium [Observations on the comparison of arcs of irrectifiable curves]. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae (лат.) . 6 : 58—84. E 252 . (Figures )Euler, Leonhard (1786). De miris proprietatibus curvae elasticae sub aequatione
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
[On the amazing properties of elastic curves contained in equation
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
Acta Academiae Scientiarum Imperialis Petropolitanae (лат.) . 1782 (2): 34—61. E 605 .Fagnano, Giulio Carlo (1718–1723). Metodo per misurare la lemniscata [Method for measuring the lemniscate]. Giornale de' letterati d'Italia (італ.) . 29 : 258—269. Giunte al primo schediasma sopra la Lemniscata . Giornale de' letterati d'Italia . 34 : 197—207. 1710.Metodo per misurare la lemniscata, schediasma II . Giornale de' letterati d'Italia . 30 : 87—111. 1710.Fagnano (1911 1850). Opere Matematiche, vol. 2 (Figures )Greenhill, Alfred George (1892). The Applications of Elliptic Functions Guyou, Émile (1887). Nouveau système de projection de la sphère: Généralisation de la projection de Mercator [New system of projection of the sphere]. Annales Hydrographiques . Série 2 (фр.) . 9 : 16—35. Houzel, Christian (1978). Fonctions elliptiques et intégrales abéliennes [Elliptic functions and Abelian integrals]. У Dieudonné, Jean (ред.). Abrégé d'histoire des mathématiques, 1700–1900. II (фр.) . Hermann. с. 1—113. Hyde, Trevor (2014). A Wallis product on clovers (PDF) . The American Mathematical Monthly . 121 (3): 237—243. doi :10.4169/amer.math.monthly.121.03.237 . S2CID 34819500 . Kubota, Tomio (1964). Some arithmetical applications of an elliptic function. Crelle's Journal . 1964 (214/215): 141—145. doi :10.1515/crll.1964.214-215.141 . S2CID 115823187 . Langer, Joel C.; Singer, David A. (2010). Reflections on the Lemniscate of Bernoulli: The Forty-Eight Faces of a Mathematical Gem (PDF) . Milan Journal of Mathematics . 78 (2): 643—682. doi :10.1007/s00032-010-0124-5 . S2CID 1448521 . Langer, Joel C.; Singer, David A. (2011). The lemniscatic chessboard . Forum Geometricorum . 11 : 183—199. Lawden, Derek Frank (1989). Elliptic Functions and Applications . Applied Mathematical Sciences. Т. 80. Springer-Verlag. doi :10.1007/978-1-4757-3980-0 . ISBN 978-1-4419-3090-3 Lee, Laurence Patrick (1976). Conformal Projections Based on Elliptic Functions Cartographica Monograph. Т. 16. University of Toronto Press. ISBN 9780919870161 Levien, Raph (2008). The elastica: a mathematical history (PDF) (Технічний звіт). № UCB/EECS-2008-103 University of California at Berkeley. Levin, Aaron (2006). A Geometric Interpretation of an Infinite Product for the Lemniscate Constant. The American Mathematical Monthly . 113 (6): 510—520. doi :10.2307/27641976 . JSTOR 27641976 . Lindqvist, Peter; Peetre, Jaak (2001). Two Remarkable Identities, Called Twos, for Inverses to Some Abelian Integrals (PDF) . The American Mathematical Monthly . 108 (5): 403—410. doi :10.1080/00029890.2001.11919766 . JSTOR 2695794 . S2CID 43677974 . Markushevich, Aleksei Ivanovich (1966). The Remarkable Sine Functions Markushevich, Aleksei Ivanovich (1992). Introduction to the Classical Theory of Abelian Functions . Translations of Mathematical Monographs. Т. 96. American Mathematical Society. doi :10.1090/mmono/096 . ISBN 9780821841648 McGregor, John L. (2005). C-CAM: Geometric Aspects and Dynamical Formulation CSIRO Oceans and Atmosphere (Технічний звіт). № 70. McKean, Henry; Moll, Victor (1999). Elliptic Curves: Function Theory, Geometry, Arithmetic . Cambridge. ISBN 9780521582285 Milne-Thomson, Louis Melville (1964). 16. Jacobian Elliptic Functions and Theta Functions . У Abramowitz, Milton; Stegun, Irene Ann (ред.). Handbook of Mathematical Functions Neuman, Edward (2007). On Gauss lemniscate functions and lemniscatic mean (PDF) . Mathematica Pannonica . 18 (1): 77—94. Nishimura, Ryo (2015). New properties of the lemniscate function and its transformation . Journal of Mathematical Analysis and Applications . 427 (1): 460—468. doi :10.1016/j.jmaa.2015.02.066 . Ogawa, Takuma (2005). Similarities between the trigonometric function and the lemniscate function from arithmetic view point . Tsukuba Journal of Mathematics . 29 (1). doi :10.21099/tkbjm/1496164894 . Peirce, Charles Sanders (1879). A Quincuncial Projection of the Sphere . American Journal of Mathematics . 2 (4): 394—397. doi :10.2307/2369491 . JSTOR 2369491 . Popescu-Pampu, Patrick (2016). What is the Genus? . Lecture Notes in Mathematics. Т. 2162. Springer. doi :10.1007/978-3-319-42312-8 . ISBN 978-3-319-42311-1 Prasolov, Viktor; Solovyev, Yuri (1997). 4. Abel's Theorem on Division of Lemniscate. Elliptic functions and elliptic integrals . Translations of Mathematical Monographs. Т. 170. American Mathematical Society. doi :10.1090/mmono/170 . ISBN 9780821805879 Rančić, Miodrag; Purser, R. James; Mesinger, Fedor (1996). A global shallow-water model using an expanded spherical cube: Gnomonic versus conformal coordinates. Quarterly Journal of the Royal Meteorological Society . 122 (532): 959—982. Bibcode :1996QJRMS.122..959R . doi :10.1002/qj.49712253209 . William P.; Walker, Peter L. (2010), "22. Jacobian Elliptic Functions", in Olver, Frank W. J.; et al. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
William P.; Walker, Peter L. (2010), "23. Weierstrass Elliptic and Modular Functions", in Olver, Frank W. J.; et al. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Robinson, Paul L. (2019a). The Lemniscatic Functions. arXiv :1902.08614 Robinson, Paul L. (2019b). The Elliptic Functions in a First-Order System. arXiv :1903.07147 Rosen, Michael (1981). Abel's Theorem on the Lemniscate. The American Mathematical Monthly . 88 (6): 387—395. doi :10.2307/2321821 . JSTOR 2321821 . Schappacher, Norbert (1997). Some milestones of lemniscatomy (PDF) . У Sertöz, S. (ред.). Algebraic Geometry (Proceedings of Bilkent Summer School, August 7–19, 1995, Ankara, Turkey). Marcel Dekker. с. 257—290. Schneider, Theodor (1937). Arithmetische Untersuchungen elliptischer Integrale [Arithmetic investigations of elliptic integrals]. Mathematische Annalen (нім.) . 113 (1): 1—13. doi :10.1007/BF01571618 . S2CID 121073687 . Schwarz, Hermann Amandus (1869). Ueber einige Abbildungsaufgaben [About some mapping problems]. Crelle's Journal (нім.) . 1869 (70): 105—120. doi :10.1515/crll.1869.70.105 . S2CID 121291546 . Siegel, Carl Ludwig (1969). 1. Elliptic Functions. Topics in Complex Function Theory, Vol. I . Wiley-Interscience. с. 1—89. ISBN 0-471-60844-0 MR 0257326 . Snape, Jamie (2004). Bernoulli's Lemniscate . Applications of Elliptic Functions in Classical and Algebraic Geometry (Дипломна робота). University of Durham. с. 50—56. Southard, Thomas H. (1964). 18. Weierstrass Elliptic and Related Functions . У Abramowitz, Milton; Stegun, Irene Ann (ред.). Handbook of Mathematical Functions Sridharan, Ramaiyengar (2004). Physics to mathematics: from lintearia to lemniscate – I (PDF) . Resonance . 9 (4): 21—29. doi :10.1007/BF02834853 . S2CID 122132138 . From lintearia to lemniscate II: Gauss and Landen's Work (PDF) . Resonance . 9 (6): 11—20. 2004. doi :10.1007/BF02839214 . S2CID 121521515 .Todd, John (1975). The lemniscate constants. Communications of the ACM . 18 (1): 14—19. doi :10.1145/360569.360580 . S2CID 85873 . Vigren, Erik; Dieckmann, Andreas (21 червня 2020). Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges . Symmetry . 12 (6): 1040. Bibcode :2020Symm...12.1040V . doi :10.3390/sym12061040 Whittaker, Edmund Taylor; Watson, George Neville (1920 ed. 1902). 22.8 The lemniscate functions . A Course of Modern Analysis





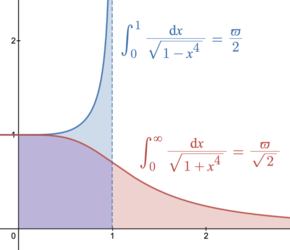





































![{\displaystyle r\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d4a8acea9f5c4e59d8f5fd0ea3c695efa7252fe)



























![{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {{\rm {d}}t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {{\rm {d}}t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {{\rm {d}}t}{\sqrt {t-t^{3}}}}\\&=4\int _{0}^{\infty }\left({\sqrt[{4}]{1+t^{4}}}-t\right)\,{\rm {d}}t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {{\rm {d}}t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,{\rm {d}}t\\&=2K({\rm {i}})={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\sqrt {\pi }}{\rm {e}}^{\beta '(0)}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\&=2{,}62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60adc27dcb890c4c8fc89ae3a2dc9edb4ebc2fcc)














![{\displaystyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\,{\rm {d}}x={\tfrac {1}{n}}\pi _{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fcf8c315f197b834e86977be2807c0e264ef389)

















![{\displaystyle {\begin{aligned}\sum _{z\in \mathbb {Z} [{\rm {i}}]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}({\rm {i}})={\frac {\varpi ^{4}}{15}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0d476dfae7978434ca359c54a2fc93b22c28798)
![{\displaystyle \mathbb {Z} [{\rm {i}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8484c4990a69790852c11b07f5fb8c2475c929d2)


















































![{\displaystyle {\mathcal {O}}=\mathbb {Z} [{\rm {i}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b508ca849d6745d1b76ec6524edeaa976c39143f)









![{\displaystyle P_{\beta }(x),Q_{\beta }(x)\in {\mathcal {O}}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15b4185e4f3e8e88d5267f62df83d2fb3c5ac76)


![{\displaystyle {\begin{aligned}\Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta }),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/688c0058aaac458e98f2517e3c571e83ded8fc49)

![{\displaystyle [\delta _{\beta }]\in (1/\beta )L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de59f86e4048a4d600ec02da0450b6f5e318429b)
![{\displaystyle [\delta _{\beta }]\in (1/\beta )L/L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcd7c658068f96d8253e40d98ca73fa28cc21068)




![{\displaystyle \Lambda _{\beta }(x)\in {\mathcal {O}}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96abdb3c8466ca26c4e6f40898b4d2e0415cf31)


![{\displaystyle {\begin{aligned}\Phi _{n}(x)=\prod _{[a]\in (\mathbb {Z} /n\mathbb {Z} )^{\times }}\left(x-{\rm {e}}^{2a\pi {\rm {i}}/n}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/557c89a75d951ecdc284198dfc6c7f7767186ee2)


![{\displaystyle \mathbb {K} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2c677cb3a6dab9be8d09aa08d78a137e17d894)



![{\displaystyle {\begin{aligned}\operatorname {sl} {\frac {2\varpi }{5}}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3ca8e6fe2e6d806f9031d7b7893c9eff066ea5)












![{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1)\left({\sqrt {{\sqrt {5}}+2}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78842c8c6060cec842d54b0d525503c394649a75)
![{\displaystyle {\tfrac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}-1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb58c50fee1e991176bb324599b4d43947c6c28)

![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c74fc1a430f5e7bb0244a281a1d4f1d0647ca67)
![{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e7446bf7046ae049852dbd22d5dc78e374b060)



![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aa6255bad54d95861f1c91c7dae1110c139d67f)
![{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}+1-{\sqrt {5}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f758a0ba20b6e2b74b2b639c48d58573c86bb7)


![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e0a7a05939422e6aadd7a3aa97292b6c764ccc)
![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d116792170cb8e87e734f4ede9d92de41a374c5c)

![{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}-1+{\sqrt {5}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee79a058fcbe0a7ca46be4da520abb70225a15f)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99990d06fac9e81d0fe3fc2d3f75ff0ebd59f28d)






































![{\displaystyle {\begin{aligned}\prod _{k=1}^{n}\operatorname {sl} \left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)={\sqrt[{8}]{\frac {\lambda ((2n+1){\rm {i}})}{1-\lambda ((2n+1){\rm {i}})}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fec7cdf2d1a7d3e7a873524806ca11e5c2fdcb94)
![{\displaystyle {\begin{aligned}&\operatorname {sl} {\bigl (}{\tfrac {1}{14}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\operatorname {sl} {\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}={\sqrt[{8}]{\frac {\lambda (7{\rm {i}})}{1-\lambda (7{\rm {i}})}}}=\operatorname {tg} {\Bigl (}{\tfrac {1}{2}}\operatorname {arccsc} {\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )},\\&\operatorname {sl} {\bigl (}{\tfrac {1}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {3}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {5}{18}}\varpi {\bigr )},\operatorname {sl} {\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}={\sqrt[{8}]{\frac {\lambda (9{\rm {i}})}{1-\lambda (9{\rm {i}})}}}=\operatorname {tg} {\Biggl (}{\frac {\pi }{4}}-\operatorname {arctg} {\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/766a1908cbc1f92b9ba3fc7b2197a645731d2da8)


















![{\displaystyle {\begin{aligned}&\operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=f\left({\frac {4\pi }{\varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\operatorname {ch} [(2n-1)\pi ]}{\operatorname {ch} ^{2}[(2n-1)\pi ]-\cos ^{2}x}}\right),\\&\operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)=f\left({\frac {4\pi }{\varpi }}\cos x\sum _{n=1}^{\infty }{\frac {\operatorname {ch} [(2n-1)\pi ]}{\operatorname {ch} ^{2}[(2n-1)\pi ]-\sin ^{2}x}}\right),\\&\operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=2{\rm {e}}^{-\pi /4}\sin x\prod _{n=1}^{\infty }{\frac {1-2{\rm {e}}^{-2n\pi }\cos 2x+{\rm {e}}^{-4n\pi }}{1+2{\rm {e}}^{-(2n-1)\pi }\cos 2x+{\rm {e}}^{-(4n-2)\pi }}},\\&\operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)=2{\rm {e}}^{-\pi /4}\cos x\prod _{n=1}^{\infty }{\frac {1+2{\rm {e}}^{-2n\pi }\cos 2x+{\rm {e}}^{-4n\pi }}{1-2{\rm {e}}^{-(2n-1)\pi }\cos 2x+{\rm {e}}^{-(4n-2)\pi }}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30456a2d555fd5e317c1fefdfd63fe23028fe9a8)











![{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f119a40d6612bf47dcb0933374839dd5372e26)

![{\displaystyle {\begin{aligned}&\int {\frac {1}{\sqrt {1-x^{4}}}}{\rm {d}}x=\operatorname {arcsl} x,\\&\int {\frac {1}{\sqrt {{\big (}x^{2}+1{\big )}{\big (}2x^{2}+1{\big )}}}}{\rm {d}}x=\operatorname {arcsl} {\frac {x}{\sqrt {x^{2}+1}}},\\&\int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}{\rm {d}}x=\operatorname {arcsl} {\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}},\\&\int {\frac {1}{\sqrt {x^{4}+1}}}{\rm {d}}x={\sqrt {2}}\operatorname {arcsl} {\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}1-x^{4}{\big )}^{3}}}}{\rm {d}}x={\sqrt {2}}\operatorname {arcsl} {\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}x^{4}+1{\big )}^{3}}}}{\rm {d}}x=\operatorname {arcsl} {\frac {x}{\sqrt[{4}]{x^{4}+1}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}1-x^{2}{\big )}^{3}}}}{\rm {d}}x=2\operatorname {arcsl} {\frac {x}{1+{\sqrt {1-x^{2}}}}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}x^{2}+1{\big )}^{3}}}}{\rm {d}}x=2\operatorname {arcsl} {\frac {x}{{\sqrt {x^{2}+1}}+1}},\\&\int {\frac {1}{\sqrt[{4}]{{\big (}ax^{2}+bx+c{\big )}^{3}}}}{\rm {d}}x={\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} {\frac {2ax+b}{{\sqrt {4a{\big (}ax^{2}+bx+c{\big )}}}+{\sqrt {4ac-b^{2}}}}},\\&\int {\sqrt {\operatorname {sech} x}}{\rm {d}}x=2\operatorname {arcsl} {\big (}\operatorname {th} {\tfrac {1}{2}}x{\big )},\\&\int {\sqrt {\sec x}}{\rm {d}}x=2\operatorname {arcsl} {\big (}\operatorname {tg} {\tfrac {1}{2}}x{\big )}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5eab9ef8dc558f5fd3de5e63b417c5bd43cf06)








![{\displaystyle {\begin{aligned}\operatorname {slh} z={\frac {1-{\rm {i}}}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+{\rm {i}}}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f3e8f7e5c5ff0bd124675cab580ea7f66184799)
![{\displaystyle {\begin{aligned}\operatorname {sinh} z=-{\rm {i}}\sin({\rm {i}}z)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f781975632aef353479b5ee97e427de2b2d346ca)



































