Еліптична крива

Еліптична крива над полем K — це множина точок проективної площини над K, що задовольняють рівнянню
разом з точкою на нескінченності та не містить особливих точок.
Еліптичні криві є одним з основних об'єктів вивчення в сучасній теорії чисел і криптографії. Наприклад, вони були використані при доведенні Великої теореми Ферма. Еліптична криптографія є самостійним розділом криптографії, що присвячений вивченню криптосистем на базі еліптичних кривих. Еліптичні криві також застосовуються в деяких алгоритмах факторизації (наприклад Алгоритм Ленстри[en]) і тестування простоти чисел. Зокрема, у класичній механіці за допомогою їх можна описати рух дзиґи.[1]
Еліпс не є еліптичною кривою. Термін «еліптична крива» походить від терміну «еліптичний інтеграл».
Еліптичні криві над дійсними числами[ред. | ред. код]

Формальне визначення еліптичної кривої важке для розуміння і вимагає деяких знань з алгебричної геометрії, але деякі властивості еліптичних кривих над дійсними числами можна описати, використовуючи тільки початкові знання з алгебри та геометрії.
Рівняння еліптичної кривої над дійсними числами можна спростити до вигляду (називається рівнянням Вейєрштрасса):
- ,
де і — дійсні числа.
Визначення еліптичної кривої також вимагає, щоб така крива не мала особливих точок. Геометрично це значить, що графік не повинен мати каспів та самоперетинів. Алгебрично це виконується тоді і тільки тоді, коли дискримінант
не дорівнює нулю. Хоч коефіцієнт -16 не впливає на визначення того, чи має крива особливі точки, але він використовується при більш глибокому вивчені еліптичних кривих.
Графік кривої без особливих точок складається з двох частин, якщо її дискримінант додатний, та з однієї — якщо від'ємний. Наприклад, для графіків на рисунку в першому випадку дискримінант дорівнює , а в другому — .
Груповий закон[ред. | ред. код]


При роботі в проективному просторі можна побудувати групову структуру на будь-якій кубічній кривій. Крива, яка задовольняє рівняння у вигляді Вейєрштрасса, матиме точку на нескінченності з однорідними координатами , яка буде нейтральним елементом в групі.
Оскільки крива симетрична відносно осі абсцис, то для будь-якої скінченної точки протилежною до неї точку можна визначити як симетричну точку відносно осі абсцис. Для буде .
Якщо та — дві точки на кривій, то ми можемо однозначно описати третю точку наступним чином: спочатку проведемо пряму через точки та . Ця пряма перетне криву також у третій точці . Далі візьмемо рівною .
Отримане визначення додавання точок працює за винятком кількох спеціальних випадків, пов'язаних з точкою на нескінченності та кратністю перетину. Далі визначимо . Це робить нейтральним елементом групи. Потім, якщо та протилежні, то визначимо . У випадку, коли буде тільки одна точка, через яку проведемо дотичну до кривої. У більшості випадків дотична буде перетинати криву у другій точці , візьмемо її як протилежну до . Однак, якщо буде точкою перегину, то за візьмемо , і в цьому випадку буде .
Для кубічної кривої, яка не задовольняє рівняння у вигляді Вейєрштрасса, все ще можна побудувати групову структуру, визначивши одну з дев'яти точок перегину як нейтральний елемент . У проективній площині кожна пряма перетинає криву у трьох точках з урахуванням кратності. Для точки протилежна їй визначається як третя точка на прямій, що проходить через та . Тоді для будь-яких точок та сума визначається як , де є третьою з точок, у яких пряма, що проходить через та , перетинає криву.
Нехай - поле, над яким визначається еліптична крива, позначимо цю криву через . Тоді -раціональні точки[en] - це точки на , координати яких з , та містять точку на нескінченності. Отримана множина -раціональних точок позначається через . Вона також утворює групу, оскільки властивості алгебричних рівнянь показують, що якщо знаходиться в , то і також є в , та якщо принаймні дві точки з трьох , і містяться в , то і третя теж. Крім того, якщо є підполем , то є підгрупою .
Вищеописану групу можна визначити як алгебраїчно, так і геометрично. Нехай крива задовольняє рівняння над полем (характеристика якого не рівна 2, 3), точки та лежать на цій кривій. Спочатку розглянемо випадок, коли (перший рисунок нижче). Нехай — пряма, що проходить через P і Q, тоді вона матиме такий кутовий коефіцієнт:
Оскільки — поле, то визначений. Рівняння прямої та рівняння кривої мають однакові значення у точках , та .
яке еквівалентне . Ми знаємо, що це рівняння має корені , та . Запишемо
З прирівняння коефіцієнтів при та з рівняння прямої через дві точки знаходимо значення та . Таким чином отримаємо , де
- ,
- .
Звідси
- ,
- .
Якщо , то існує два варіанти:
- 1) (третій та четвертий рисунки нижче), включаючи випадок, коли (четвертий рисунок), тоді сума точок та дорівнюватиме . Таким чином протилежною до кожної точки є точка симетрична відносно осі .
- 2) , тоді та (другий рисунок) знаходиться наступним чином:
- ,
- ,
- .
Звідси
- ,
- .
Еліптичні криві над полем комплексних чисел[ред. | ред. код]
Формулювання еліптичних кривих як вкладення тора в комплексну проективну площину випливає безпосередньо з властивості еліптичних функцій Вейєрштрасса. Ці функції і їх перші похідні пов'язані формулою:
- .
Тут і — константи; — еліптична функція Вейєрштрасса, а — її похідна. Видно, що співвідношення—у вигляді еліптичної кривої (над комплексними числами). Функції Вейерштрасса двічі періодичні; тобто, вони є періодичними у відношенні ґратки По суті, функції Вейєрштрасса натурально визначені на торі . Цей тор може бути вкладений в комплексну проектну площину відображенням
- .
Це відображення — груповий ізоморфізм, що відображає структуру натуральної групи тора в проективну площину. Крім того, це ізоморфізм поверхонь Рімана, тобто, топологічно, дану еліптичну криву можна розглянути як тор. Якщо ґратка пов'язана із ґраткою множенням на ненульове комплексне число , то відповідні криві ізоморфні. Класи ізоморфізму еліптичних кривих визначені j-інваріантом.
Класи ізоморфізму можна розглянути простішим способом. Константи і , що називаються модулярними інваріантами, єдиним чином визначені структурою тора. Втім, комплексні числа є полем розкладу для многочленів, а значить, еліптичні криві можна записати як
- .
Можна показати, що
і
- ,
отже модулярний дискримінант рівний
- .
Тут λ іноді називають модулярною лямбда-функцією.
Зв'язок з теорією чисел[ред. | ред. код]
Теорема Морделла — Вейля[en] стверджує, що якщо поле — поле раціональних чисел (або, взагалі числовим полем), то група -раціональних точок є скінченно породженою. Це означає, що група може бути виражена як пряма сума вільної абелевої групи і скінченної підгрупи кручення. Хоч і відносно легко визначити підгрупу кручення , але немає загального алгоритму для обчислення рангу вільної підгрупи. Формула для обчислення рангу дається в гіпотезі Бірча і Свіннертона-Дайера.
Недавнє доведення Великої теореми Ферма було зроблено за допомогою доведення особливого випадку теореми Таніями — Шимури, про зв'язок еліптичних кривих над раціональними числами з модулярними формами; ця теорема згодом була доведена і в цілому.
Точне число раціональних точок еліптичної кривої над скінченним полем достатньо важко обчислити, але теорема Хассе стверджує, що
- .
Число точок на даній кривій може бути обчислено за допомогою алгоритму Шуфа.
Еліптичні криві над довільним полем[ред. | ред. код]
Еліптичні криві можуть бути визначені над довільним полем ; формально, еліптична крива визначається як невироджена проектна алгебрична крива над з родом 1 з заданою точкою, визначеною над .
Якщо характеристика поля не рівна 2 та 3, то будь-яка еліптична крива над може бути записана у вигляді
- ,
де і — такі елементи , що многочлен (права сторона) не має кратного кореня. Якщо характеристика рівна 2 або 3, то необхідно ввести ще декілька умов: якщо характеристика поля дорівнює 3, то загальне рівняння можна звести до вигляду
- ,
де , , — константи, і поліном праворуч має тільки прості корені (позначення обрано з історичних причин). У полі характеристики 2 багато чого неможливо, тому загальне рівняння залишається без змін
за умови, що точки, які його задовольняють не будуть особливими. Якби характеристика не була перешкодою, то кожне рівняння зменшилось би до попереднього шляхом заміни змінних.
Можна узяти криву як множину всіх точок , які задовольняють вищезгаданому рівнянню, а і одночасно є елементами алгебричного замикання поля . Точки кривої, обидві координати яких належать , називаються -раціональними точками.
Еліптичні криві над скінченним полем[ред. | ред. код]
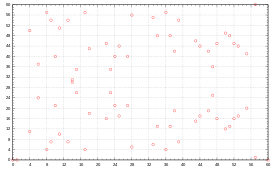
Нехай скінченне поле з елементів та еліптична крива визначена над . Точну кількість раціональних точок еліптичної кривої над взагалі досить важко обчислити. Теорема Гассе про еліптичні криві дає, враховуючи точку на нескінченності, таку оцінку:
Іншими словами, кількість точок кривої зростає приблизно так само як кількість елементів у полі.

Множина точок — скінченна абелева група. Вона завжди циклічна або ізоморфна прямій сумі двох циклічних груп. [2] Наприклад,[3] крива, визначена рівнянням , над полем має 72 точки (71 скінченних точок враховуючи та одна точка на нескінченності) та ізоморфна . Кількість точок на певній кривій можна обчислити через алгоритм Шуфа.
Вивчення кривої над розширеннями поля полегшується введенням локальної дзета-функції для , визначеної наступним чином
- ,
де поле — це (з точністю до ізоморфізму) розширення поля степеня n (тобто ). Ця дзета-функція є раціональною функцією від T. Існує ціле число таке, що
Крім того,
де і . Цей результат є окремим випадком гіпотез Вейля. Наприклад,[4] дзета-функція для над полем дорівнює
це випливає з того, що
- .
Застосування[ред. | ред. код]
Еліптичні криві над скінченними полями використовуються в криптографії (див. Еліптична криптографія) та при факторизації великих цілих чисел. Ці застосунки зазвичай використовують групову структуру на точках еліптичної кривої.
З 1998 року використовування еліптичних кривих для розв'язування криптографічних завдань, таких як цифровий підпис, було закріплено у стандартах США ANSI X9.62 та FIPS 186–2. В Україні ухвалений стандарт цифрового підпису базується на еліптичних кривих ДСТУ 4145-2002[5].
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ Adler M., van Moerbeke P., Vanhaecke P. (2004). [Integrable Spinning Tops. In: Algebraic Integrability, Painlevé Geometry and Lie Algebras Integrable Spinning Tops. In: Algebraic Integrability, Painlevé Geometry and Lie Algebras]. Springer, Berlin, Heidelberg. ISBN 978-3-642-06128-8.
- ↑ Washington, Lawrence C. Elliptic curves: number theory and cryptography. CRC press, 2008. - c. 97
- ↑ Koblitz 1994, p. 158
- ↑ Koblitz 1994, p. 160
- ↑ М. В. Захарченко, О. В. Онацький, Л. Г. Йона, Т. М. Шинкарчук (2011). 2.12 Криптосистема на еліптичних кривих. Асиметричні методи шифрування в телекомунікаціях. ОНАЗ ім. О. С. Попова. ISBN 978-966-7598-71-6.
Література[ред. | ред. код]
- Н. Коблиц (2001). Курс теории чисел и криптографии = A Course in Number Theory and Cryptography. Научное издательство «ТВП». ISBN 5-85484-014-6.
{{cite book}}: Cite має пусті невідомі параметри:|1=та|2=(довідка) - Н. Коблиц (2000). Введение в эллиптические кривые и модулярные формы = Introduction to Elliptic Curves and Modular Forms. ИО НФМИ. ISBN 5-8032-3325-0.
{{cite book}}: Cite має пусті невідомі параметри:|1=та|2=(довідка) - С. Ленг (2000). Эллиптические функции = Elliptic functions. ИО НФМИ. ISBN 5-8032-3326-9.
{{cite book}}: Cite має пусті невідомі параметри:|1=та|2=(довідка) - Joseph H. Silverman (1986). The Arithmetic of Elliptic Curves. Springer. ISBN 0-387-96203-4.
{{cite book}}: Cite має пусті невідомі параметри:|1=та|2=(довідка) - Lawrence Washington (2003). Elliptic Curves: Number Theory and Cryptography. Chapman & Hall/CRC. ISBN 1-58488-365-0.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Це незавершена стаття з криптографії. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (серпень 2017) |






























































































![{\displaystyle Z(E(K),T)\equiv \exp \left(\sum _{n=1}^{\infty }\#\left[E(K_{n})\right]{T^{n} \over n}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/681ace7ed092de951fed6ed9e0fcec88e6cc2e32)









