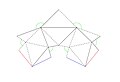
Згинаний многогранник

Многогранник (точніше — многогранна поверхня) називається зги́наною, якщо її просторову форму можна змінити такою безперервною в часі деформацією, за якої кожна грань не змінює своїх розмірів (тобто рухається як тверде тіло), а деформація здійснюється тільки за рахунок безперервної зміни двогранних кутів. Така деформація називається безперервним згинанням многогранника.

Властивості та приклади

У теорії зги́наних многогранників відомо чимало красивих і нетривіальних тверджень. Нижче наведено найважливіші зі встановлених на сьогодні фактів, дотримуючись хронологічного порядку:

1. Ніякий опуклий многогранник не може згинатись. Це негайно випливає з теореми Коші про однозначну визначеність опуклого многогранника, доведену в 1813 році.
2. Перші приклади згинаних многогранників були побудовані бельгійським інженером і математиком Раулем Брікаром в 1897 році. Зараз їх називають октаедрами Брікара. Вони не тільки неопуклі, але й мають самоперетини, що не дозволяє побудувати їх картонну модель, що рухається.
3. У 1976 році американський математик Роберт Коннеллі вперше побудував згинаний многогранник без самоперетинів.
4. З усіх відомих на сьогоднішній день згинаних многогранників без самоперетинів найменше число вершин (дев'ять) має многогранник, побудований німецьким математиком Клаусом Штеффеном (нім. Klaus Steffen) .
5. Відомі приклади згинаних многогранників, які є реалізаціями тора або пляшки Клейна, або взагалі двовимірної поверхні будь-якого топологічного роду.
6. З формули Шлефлі випливає, що будь згинаний многогранник в процесі згинання зберігає так звану інтегральну середню кривину, тобто число, рівне $\sum |\ell |(\pi -\alpha (\ell ))$, де $|\ell |$ — довжина ребра $~\ell$, $~\alpha (\ell )$ — величина внутрішнього двогранного кута при ребрі $~\ell$, а сума поширюється на всі ребра многогранника. Див також.
7. Теорема Сабітова: Будь-який згинаний многогранник в процесі згинання зберігає свій об'єм, тобто він буде згинатися навіть якщо його заповнити нестисливої ​​рідиною.

• 
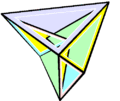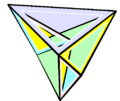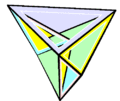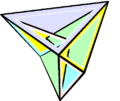
  октаедр Брікара, що згинається, першого типу
• 
  октаедр Брікара, що згинається, другого типу
• 
  Згинаний многогранник Штеффена
• 
  Розгортка згинаного многогранника Штеффена

Гіпотези

Незважаючи на значний прогрес, в теорії згинаних многогранників залишається багато невирішених проблем. Ось кілька відкритих гіпотез:

1. многогранник Штеффена має найменше число вершин серед усіх згинаних многогранників, що не мають самоперетинів;
2. Якщо один многогранник, який не має самоперетинів, отриманий з іншого многогранника, який також не має самоперетинів, безперервним згинанням, то ці многогранники рівноскладені, тобто перший можна розбити на скінченне число тетраедрів, кожен з цих тетраедрів незалежно від інших можна пересунути в просторі і отримати розбиття другого многогранника.

Узагальнення

Все сказане вище відносилося до многогранників в тривимірному евклідовому просторі. Однак дане вище визначення згинаного многогранника можна застосувати і до багатовимірних просторів і до неевклідових просторів, таких як сферичний простір і простір Лобачевського. Для них також відомі як нетривіальні теореми, так і відкриті запитання. Наприклад:

1. Доведено, що в чотиривимірному евклідовому просторі, просторі Лобачевського розмірності 3 та 4, а також в сферичному просторі розмірності 3 та 4 є згинані многогранники, в той час як існування згинаних многогранників в евклідових просторах розмірності 5 і вище залишається відкритим питанням ;
2. Доведено, що будь-який згинаний многогранник в евклідовому просторі розмірності 3 і вище зберігає свою інтегральну середню кривину в процесі згинання, але невідомо чи всякий згинаний многогранник в евклідовому просторі розмірності 4 і вище зберігає свій об'єм в процесі згинання;
3. Доведено, що в тривимірному сферичному просторі існує згинаний многогранник, обсяг якого непостійний у процесі згинання, але не відомо чи обов'язково зберігається обсяг згинаного многогранника в тривимірному просторі Лобачевського.

Зроби сам

Зробити модель згинаного многогранника Штеффена зовсім не важко. Опишемо це процес крок за кроком.

• Збережіть файл з розгорткою многогранника Штеффена з наведеної вище «галереї зображень».
• Збільшите розгортку в 2-3 рази і роздрукуйте його на принтері (при цьому бажано використовувати щільний папір або напівкартон).
• Виріжте розгортку по контуру, що складається з червоних, синіх і чорних (суцільних і пунктирних) відрізків.
• Кілька разів перегніть папір по суцільним і пунктирним відрізкам, що залишилися на розгортці. Виконуючи наступні дії слід надавати поверхні таку форму, щоб суцільні відрізки були «гірськими хребтами» (тобто виступали з многогранника назовні), а пунктирні відрізки були «долинами» (тобто вдавалися б всередину многогранника).
• Зігніть поверхню в просторі і склейте між собою кожні два чорних відрізка, з'єднаних на розгортці зеленої дугою кола.
• Склейте між собою два синіх відрізка.
• Склейте між собою два червоних відрізка.

Модель многогранника Штеффена готова.

Популярна література

• В. А. Александров, Изгибаемые многогранные поверхности, Соросовский образовательный журнал. 1997. No. 5. С. 112–117. Ця ж стаття перевидана в книзі під редакцією В. Н. Сойфера и Ю. П. Соловьёва: Современное естествознание. Энциклопедия. Т. 3: Математика и механика М.: Наука, М.: Флинта, 2000. ISBN 5-02-004299-4.
• М. Берже, Геометрія. М.: Мир, 1984. Т. 1. С. 516–517.
• В. А. Залгаллер, Непрерывно изгибаемый многогранник, Квант. 1978. No. 9. С. 13—19.
• А. И. Медяник, Модель многогранника Коннелли, Квант. 1979. No. 7. С. 39.
• И.Х. Сабитов,. Объёмы многогранников. — М.:МЦНМО, 2002.
• Девид А. Кларнер. Математичний квітник. Збірник статей і задач = The Mathematical Gardner / Пер. с англ. Ю. А. Данилова; под ред., с предисл. и прилож. И. М. Яглома. — М : Мир, 1983. — С. 105—117.

Наукова література

• В. А. Александров, Новый пример изгибаемого многогранника, Сиб. мат. журн. 1995. Т. 36, No 6. С. 1215–1224.
• Н. Х. Кьойпер, Згинні поліедральні сфери в $~E^{3}$, по Роберту Коннеллі, в кн. під ред. А. М. Колмогорова і С. П. Новикова: Исследования по метрической теории поверхностей. М.: Мир. 1980. С. 210–227.
• P. Коннеллі, Про один підхід до проблеми незгинності. Там же. С. 164–209.
• Р. Коннеллі, Деякі припущення і невирішені питання в теорії згинань. Там же. С. 228–238.
• И. Г. Максимов, Неизгибаемые многогранники с малым количеством вершин, Фундам. прикл. матем. 2006. Т. 12, No. 1. С. 143–165.
• С. Н. Михалёв, Некоторые необходимые метрические условия изгибаемости подвесок, Вестник МГУ, Сер. I, 2001, No. 3, 15—21.
• И. Х. Сабитов, Объём многогранника как функция его метрики, Фундам. прикл. матем. 1996. Т. 2, No. 4. С. 1235–1246.
• И. Х. Сабитов, Обобщённая формула Герона — Тарталья и некоторые её следствия, Матем. сб. 1998. Т. 189, No. 10. С. 105–134.