Хі
Функція розподілу ймовірностей
Параметри
k
>
0
{\displaystyle k>0\,}
Носій функції
x
∈
[
0
,
∞
)
{\displaystyle x\in [0,\infty )}
Розподіл імовірностей
1
2
(
k
/
2
)
−
1
Γ
(
k
/
2
)
x
k
−
1
e
−
x
2
/
2
{\displaystyle {\frac {1}{2^{(k/2)-1}\Gamma (k/2)}}\;x^{k-1}e^{-x^{2}/2}}
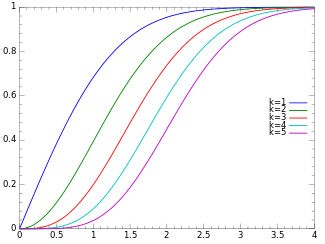
Функція розподілу ймовірностей (cdf)
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle P(k/2,x^{2}/2)\,}
Середнє
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Медіана
≈
k
(
1
−
2
9
k
)
3
{\displaystyle \approx {\sqrt {k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}}}}
Мода
k
−
1
{\displaystyle {\sqrt {k-1}}\,}
k
≥
1
{\displaystyle k\geq 1}
Дисперсія
σ
2
=
k
−
μ
2
{\displaystyle \sigma ^{2}=k-\mu ^{2}\,}
Коефіцієнт асиметрії
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Коефіцієнт ексцесу
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle {\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Ентропія
ln
(
Γ
(
k
/
2
)
)
+
{\displaystyle \ln(\Gamma (k/2))+\,}
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle {\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}
Твірна функція моментів (mgf)Складна (див. текст) Характеристична функція Складна (див. текст)
У теорії ймовірностей та статистиці розподіл хі є неперервним розподілом ймовірностей . Це розподіл додатньої частини квадратного кореня з суми квадратів набору незалежних випадкових величин, кожна з яких має стандартний нормальний розподіл , або ж еквівалентно, розподіл евклідової відстані випадкових величин від початку координат. Таким чином, це пов'язано з розподілом хі-квадрат , описуючи розподіл додаткової частини квадратного кореня випадкової величини, що має розподіл хі-квадрат.
Якщо
Z
1
,
…
,
Z
k
{\displaystyle Z_{1},\ldots ,Z_{k}}
k
{\displaystyle k}
нормально розподіленмх випадкових величини із середнім значенням 0 та стандартним відхиленням 1, тоді статистика
Y
=
∑
i
=
1
k
Z
i
2
{\displaystyle Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}}}
має розподіл хі. Розподіл хі має один параметр,
k
{\displaystyle k}
Z
i
{\displaystyle Z_{i}}
Найвідоміші приклади - розподіл Релея (розподіл хі з двома ступенями свободи ) та розподіл Максвелла – Больцмана молекулярних швидкостей в ідеальному газі (розподіл хі з трьома ступенями свободи).
Функція густини ймовірності (pdf) хі-розподілу записується
f
(
x
;
k
)
=
{
x
k
−
1
e
−
x
2
/
2
2
k
/
2
−
1
Γ
(
k
2
)
,
x
≥
0
;
0
,
інакше
.
{\displaystyle f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0;\\0,&{\text{інакше}}.\end{cases}}}
де
Γ
(
z
)
{\displaystyle \Gamma (z)}
гамма-функція .
Функція розподілу задається:
F
(
x
;
k
)
=
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}
де
P
(
k
,
x
)
{\displaystyle P(k,x)}
регуляризована гамма-функція .
Твірна функція моментів задається:
M
(
t
)
=
M
(
k
2
,
1
2
,
t
2
2
)
+
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
t
2
2
)
,
{\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right),}
де
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
Характеристична функція задається:
φ
(
t
;
k
)
=
M
(
k
2
,
1
2
,
−
t
2
2
)
+
i
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
−
t
2
2
)
{\displaystyle \varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right)}
Початкові моменти задаються:
μ
j
=
∫
0
∞
f
(
x
;
k
)
x
j
d
x
=
2
j
/
2
Γ
(
(
k
+
j
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{j}=\int _{0}^{\infty }f(x;k)x^{j}dx=2^{j/2}{\frac {\Gamma ((k+j)/2)}{\Gamma (k/2)}}}
де
Γ
(
z
)
{\displaystyle \Gamma (z)}
гамма-функція . Одже, перші кілька моментів:
μ
1
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu _{1}={\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!1)/2)}{\Gamma (k/2)}}}
μ
2
=
k
{\displaystyle \mu _{2}=k\,}
μ
3
=
2
2
Γ
(
(
k
+
3
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
μ
1
{\displaystyle \mu _{3}=2{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!3)/2)}{\Gamma (k/2)}}=(k+1)\mu _{1}}
μ
4
=
(
k
)
(
k
+
2
)
{\displaystyle \mu _{4}=(k)(k+2)\,}
μ
5
=
4
2
Γ
(
(
k
+
5
)
/
2
)
Γ
(
k
/
2
)
=
(
k
+
1
)
(
k
+
3
)
μ
1
{\displaystyle \mu _{5}=4{\sqrt {2}}\,\,{\frac {\Gamma ((k\!+\!5)/2)}{\Gamma (k/2)}}=(k+1)(k+3)\mu _{1}}
μ
6
=
(
k
)
(
k
+
2
)
(
k
+
4
)
{\displaystyle \mu _{6}=(k)(k+2)(k+4)\,}
де найправіші вирази виводяться за допомогою рекуренткого відношення гамма-функції:
Γ
(
x
+
1
)
=
x
Γ
(
x
)
{\displaystyle \Gamma (x+1)=x\Gamma (x)\,}
З цих виразів ми можна вивести наступні співвідношення:
Середнє:
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Дисперсія:
V
=
k
−
μ
2
{\displaystyle V=k-\mu ^{2}\,}
Асиметрія:
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Компенсований ексцес:
γ
2
=
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle \gamma _{2}={\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Ентропія задається рівнянням:
S
=
ln
(
Γ
(
k
/
2
)
)
+
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi ^{0}(k/2))}
де
ψ
0
(
z
)
{\displaystyle \psi ^{0}(z)}
Виведемо формули наближень середнього та дисперсії розподілу хі для великих n = k + 1. Вони мають практичне застосування, наприклад, для пошуку розподілу середньоквадратичного відхилення вибірки нормально розподіленої сукупності, де n - обсяг вибірки.
Тоді середнє значення:
μ
=
2
Γ
(
n
/
2
)
Γ
(
(
n
−
1
)
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,\,{\frac {\Gamma (n/2)}{\Gamma ((n-1)/2)}}}
Застосувавши формулу дублювання Лежандра можемо подати:
2
n
−
2
Γ
(
(
n
−
1
)
/
2
)
⋅
Γ
(
n
/
2
)
=
π
Γ
(
n
−
1
)
{\displaystyle 2^{n-2}\,\Gamma ((n-1)/2)\cdot \Gamma (n/2)={\sqrt {\pi }}\Gamma (n-1)}
тож:
μ
=
2
/
π
2
n
−
2
(
Γ
(
n
/
2
)
)
2
Γ
(
n
−
1
)
{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {(\Gamma (n/2))^{2}}{\Gamma (n-1)}}}
Використовуючи наближення Стірлінга для гамма-функції, отримаємо наступний запис середнього:
μ
=
2
/
π
2
n
−
2
(
2
π
(
n
/
2
−
1
)
n
/
2
−
1
+
1
/
2
e
−
(
n
/
2
−
1
)
⋅
[
1
+
1
12
(
n
/
2
−
1
)
+
O
(
1
n
2
)
]
)
2
2
π
(
n
−
2
)
n
−
2
+
1
/
2
e
−
(
n
−
2
)
⋅
[
1
+
1
12
(
n
−
2
)
+
O
(
1
n
2
)
]
{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}}
=
(
n
−
2
)
1
/
2
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
=
n
−
1
(
1
−
1
n
−
1
)
1
/
2
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle =(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
=
n
−
1
⋅
[
1
−
1
2
n
+
O
(
1
n
2
)
]
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
=
n
−
1
⋅
[
1
−
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
Отже, дисперсія задається:
V
=
(
n
−
1
)
−
μ
2
=
(
n
−
1
)
⋅
1
2
n
⋅
[
1
+
O
(
1
n
)
]
{\displaystyle V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]}
Якщо
X
∼
χ
k
{\displaystyle X\sim \chi _{k}}
X
2
∼
χ
k
2
{\displaystyle X^{2}\sim \chi _{k}^{2}}
розподіл хі-квадрат )
lim
k
→
∞
χ
k
−
μ
k
σ
k
→
d
N
(
0
,
1
)
{\displaystyle \lim _{k\to \infty }{\tfrac {\chi _{k}-\mu _{k}}{\sigma _{k}}}\xrightarrow {d} \ N(0,1)\,}
Нормальний розподіл )Якщо
X
∼
N
(
0
,
1
)
{\displaystyle X\sim N(0,1)\,}
|
X
|
∼
χ
1
{\displaystyle |X|\sim \chi _{1}\,}
Якщо
X
∼
χ
1
{\displaystyle X\sim \chi _{1}\,}
σ
X
∼
H
N
(
σ
)
{\displaystyle \sigma X\sim HN(\sigma )\,}
σ
>
0
{\displaystyle \sigma >0\,}
χ
2
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle \chi _{2}\sim \mathrm {Rayleigh} (1)\,}
Розподіл Релея )
χ
3
∼
M
a
x
w
e
l
l
(
1
)
{\displaystyle \chi _{3}\sim \mathrm {Maxwell} (1)\,}
Розподіл Максвелла )
‖
N
i
=
1
,
…
,
k
(
0
,
1
)
‖
2
∼
χ
k
{\displaystyle \|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}}
2-норма
k
{\displaystyle k}
k
{\displaystyle k}
розподіл хі - це окремий випадок узагальненого гамма розподілу або розподілу Накагамі або нецентрального розподілу чі
Середнє значення розподілу хі (масштабоване квадратним коренем з
n
−
1
{\displaystyle n-1}
Різні хі та хі-квадрат розподіли
Name
Statistic
Розподіл хі-квадрат
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}
Нецентрований хі-квадрат розподіл
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}
Розподіл хі
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}
Нецентрований хі розподіл
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}
Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972 .
Дискретні одновимірні Дискретні одновимірні Неперервні одновимірні Неперервні одновимірні Неперервні одновимірні Неперервні одновимірні Змішані Багатовимірні (спільні) Напрямкові Вироджені та сингулярні [en] Сімейства









































![{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ab2d5763ab73955d1da591a2c76909c453fb48)
![{\displaystyle =(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f3e1534e28ac6e9276477260c929f0fa2072a4e)
![{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f137a4f4c36c6d1a3e6e133d9ea9c8cf4cc3cfa)
![{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16110f5e6cee819cf7ce548062a398bcf57f7eac)
![{\displaystyle V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5610836c34d335011ebc02dc4ee6ec6753aac429)















