Стандартне відхилення


Станда́ртне відхи́лення (англ. standard deviation) або середнє квадратичне відхилення — у теорії ймовірностей і статистиці один із найпоширеніших показників розсіювання (розкиду) значень випадкової величини відносно її математичного сподівання, тобто центру розподілу. Має ту ж розмірність, що і випадкова величина. У літературі для позначення стандартного відхилення використовується літера грецької абетки сигма σ.
За визначенням середнє квадратичне відхилення є додатнім квадратним коренем із дисперсії. Як і дисперсія характеризує розсіяння значень навколо центру розподілу: більшому значенню стандартного відхилення відповідає більший їх розкид. Практична перевага стандартного відхилення як міри розсіяння в порівнянні з дисперсією полягає в тому, що його розмірність збігається з розмірністю випадкової величини, в той час як розмірність дисперсії — квадрат розмірності випадкової величини.
Іноді середнє квадратичне відхилення називають «стандартною похибкою» або «стандартною помилкою». Ці назви вживати не рекомендується, оскільки це може призвести до плутанини і неправильного тлумачення результатів того чи іншого дослідження.
Слід зауважити, що стандартне відхилення випадкової величини не є випадковою величиною.
Історія[ред. | ред. код]
Термін стандартне відхилення вперше у монографіях використав[1] Карл Пірсон[2] в 1894 році, перед тим почав використовувати його при читанні лекцій. Цим він замінив альтернативні назви подібного поняття, що існували раніше: наприклад, Гаусс використовував термін середня похибка.[3]
Визначення[ред. | ред. код]
Нехай — випадкова величина з математичним сподіванням μ:
- ,
де — оператор математичного сподівання.
Тоді
- ,
- де — дисперсія випадкової величини .
Отже, стандартне відхилення — це додатній квадратний корінь із дисперсії, тобто додатній квадратний корінь із математичного сподівання квадрату відхилення випадкової величини від її математичного сподівання.
Стандартне відхилення існує не для будь-якої випадкової величини. Як видно, умовою існування стандартного відхилення випадкової величини є існування її математичного сподівання. Прикладом розподілу, для якого не існує математичне сподівання, а отже не існує і стандартне відхилення, є розподіл Коші.
Неперервна випадкова величина[ред. | ред. код]
Для випадку неперервної випадкової величини з функцією густини ймовірностей формула для стандартного відхилення набуває вигляду
де — математичне сподівання, а інтеграли є невласними з границями інтегрування від до .
Приклад.
Для неперервної випадкової величини , яка рівномірно розподілена в діапазоні від -1 до + 1, стандартне відхилення
.
Тут було враховано, що в даному випадку , за межами відрізка та дорівнює 1/2 в межах цього відрізка.
Дискретна випадкова величина[ред. | ред. код]
Нехай — дискретна випадкова величина, для якої ймовірність події становить . Тоді вираз для стандартного відхилення набуває вигляду:
,
де — математичне сподівання.
Приклад.
Під час кидання грального кубика для гри в кості, якщо кубик симетричний, з однаковою ймовірністю 1/6 може випасти будь-яке число від 1 до 6. Фактично, число , що випадає під час кидання кубика, — дискретна рівномірно розподілена випадкова величина, яка може приймати цілі значення в діапазоні від 1 до 6. З урахуванням, що математичне сподівання , стандартне відхилення цієї величини .
Використання[ред. | ред. код]
Стандартне відхилення використовують під час розрахунку середнього квадратичного відхилення середнього арифметичного, для побудови довірчих інтервалів, статистичної перевірки гіпотез, виміру лінійного взаємозв'язку між випадковими величинами.
Оцінювання[ред. | ред. код]
Стандартне відхилення усієї сукупності може застосовуватися у випадках, де відібрано кожного представника сукупності (стандартизоване тестування). У випадках коли це не можливо, стандартне відхилення σ оцінюють на основі випадкової вибірки із сукупності і розраховують статистику для вибірки, яка використовуються для оцінки стандартного відхилення сукупності. Це називається статистичною оцінкою, а оцінене значення називається стандартним відхиленням вибірки, що позначається як s (іноді зі позначеннями). Однак, на відміну від випадку із оцінкою математичного сподівання для сукупності, де оцінкою для вибірки є вибіркове середнє, яке є простою оцінкою із багатьма властивостями для різних задач (незміщена, ефективна, максимальної правдоподібності), але не існує єдиної оцінки з усіма цими властивостями для стандартного відхилення, а незміщена оцінка для стандартного відхилення пов'язана із технічними складностями. Найчастіше, стандартне відхилення оцінюється за допомогою корегованого вибіркового стандартного відхилення (із використанням корекції N − 1), визначеного нижче. Однак інші оцінки можуть бути кращими за інших умов: некорегована оцінка (з використанням N) призводить до менших значень середньоквадратичної похибки, а використання N − 1.5 (для нормального розподілу) майже повністю усуває зміщення.
Некореговане стандартне відхилення для вибірки[ред. | ред. код]
Формулу для стандартного відхилення сукупності (для скінченної сукупності) можливо застосувати до вибірки, використавши як розмір вибірки розмір даної вибірки (хоча фактичний розмір сукупності для якої було отримано вибірки є набагато більшим). Ця оцінка, позначається як sN, і відома як некореговане вибіркове стандартне відхилення, або іноді стандартне відхилення вибірки (що представляє і розглядається як ціла сукупність), і визначається так:
де значення спостережень даної вибірки а середнє значення цих спостережень, а в знаменнику N означає об'єм вибірки. Середньоквадратичне відхилення — дорівнює кореню квадратному з дисперсії випадкової величини для вибірки, що в свою чергу є середнім значенням для квадратичних відхилень від вибіркового середнього.
Це конзистентна оцінка (вона збігається за імовірністю до значення, що відповідає сукупності із збільшенням об'єму вибірки до нескінченності), і ця оцінка є оцінкою максимальної правдоподібності якщо сукупність має нормальний розподіл. Однак, вона є зміщеною оцінкою, оскільки оцінені значення як правило значно занижені. Зміщення зменшується із збільшенням об'єму вибірки, зменшуючись у порядку пропорційному до 1/N, і таким чином зміщення є найбільш відчутним для малих і середніх вибірок; для зміщення буде меншим за 1 %. Таким чином, для дуже великих вибірок, це некореговане вибіркове стандартне відхилення є в загальному випадку прийнятним. Ця оцінка має також рівномірно меншу середньоквадратичну похибку ніж кореговане стандартне відхилення вибірки.
Кореговане стандартне відхилення для вибірки[ред. | ред. код]
При невеликій вибірці () вводиться поправка Бесселя:
де:
— стандартне відхилення, незміщена оцінка средньоквадратичного відхилення випадкової величини відносно її математичного сподівання;
— дисперсія;
— -й елемент вибірки;
— середнє арифметичне вибірки:
— обсяг (розмір) вибірки.
Слід звернути увагу на відмінність стандартного відхилення (у знаменнику ) від кореня з дисперсії (у знаменнику ). Для малих обсягів вибірки оцінка дисперсії є дещо зміщеною на величину , для нескінченно великого обсягу вибірки різниця між вказаними величинами зникає.
Вибірка — лише частина генеральної сукупності. Генеральна сукупність — абсолютно всі можливі результати. Отримати результат, що не входить в генеральну сукупність — неможливо. Для випадку з киданням монети генеральною сукупністю є: цифра, ребро, орел. А ось пара орел-цифра — вже лише вибірка. Для генеральної сукупності математичне очікування збігається зі справжнім значенням оцінюваного параметра. А для вибірки — необов'язково. Математичне очікування вибірки має зміщення щодо дійсного значення параметра. Через це середньоквадратична помилка більша ніж дисперсія, оскільки дисперсія — математичне очікування квадрата відхилення від середнього значення, а середньоквадратичне відхилення — математичне очікування відхилення від справжнього значення. Різниця в тому, від чого шукаємо відхилення: коли дисперсія, то від середнього (і не важливо достеменне це середнє чи помилкове), а коли середньоквадратичне відхилення, то це відхилення від справжнього середнього значення.
Незміщене вибіркове стандартне відхилення[ред. | ред. код]
На відміну від середнього і дисперсії, не існує формули незміщеної оцінки стандартного відхилення, яка б виконувалася для всіх розподілів. Замість неї, використовують s як базис, який масштабують за допомогою коефіцієнту поправки з метою утворити незміщену оцінку. Для нормального розподілу, незміщена оцінка задається як s/c4, де коефіцієнт поправки (який залежить від N) визначено за допомогою Гамма-функції, і дорівнює:
Це отримане із того, що вибірковий розподіл для стандартного відхилення вибірки відповідає (масштабованому) Хі розподілу, а коефіцієнт поправки є середнім даного хі розподілу.
Наближення можна виконати замінивши N − 1 на N − 1.5, в результаті буде отримано:
Похибка цього наближення зменшується квадратично (із 1/N2), і підходить для всіх вибірок, крім найменших або при необхідності мати найвищу точність: для N = 3 зміщення дорівнює 1.3 %, а для N = 9 зміщення уже буде меншим за 0.1 %.
Для інших розподілів, правильна формула буде залежати від розподілу, але основним правилом є використовувати таку поправку для наближення:
де γ2 означає поправку ексцесу для популяції. Цей параметр може бути або відомим заздалегідь для певного розподілу, або оціненим із даних.
Довірчий інтервал стандартного відхилення вибірки[ред. | ред. код]
Стандартне відхилення (СВ), яке ми отримуємо за допомогою вибірки розподілу, саме по собі не є абсолютно точним з двох причин: математичної (описаній тут за допомогою довірчого інтервалу) і з практичної причини вимірювання (похибки вимірювання). Математичний вплив описують за допомогою довірчого інтервалу або ДІ. Аби показати, як збільшення вибірки призведе до звуження довірчого інтервалу, наведемо такі приклади: Невелика сукупність розміром N = 2 має лише один ступінь свободи для оцінки стандартного відхилення. В результаті 95 % довірчого інтервалу для стандартного відхилення знаходиться в межах від 0.45 × СВ до 31.9 × СВ; і виглядає так:
де є p-им квантилем розподілу хі-квадрат із k ступенями свободи, а є рівнем довіри. Це є еквівалентно наступному виразу:
Із k = 1, і . Обернене значення квадратних коренів цих двох чисел дають нам множники 0.45 і 31.9 вказані вище.
Більша сукупність при N = 10 має 9 ступенів свободи при визначенні стандартного відхилення. Такий самий розрахунок, як наведено вище дозволяє отримати, що в цьому випадку 95 % ДІ знаходиться в межах від 0.69*СВ до 1.83*СВ. Тому навіть при сукупності вибірки розміром в 10, фактичне СВ може залишатися майже вдвічі більшим ніж отримане вибіркове СВ. Для сукупності вибірки N=100, це зменшується до 0.88*СВ до 1.16*СВ. Аби бути впевненим, що вибіркове стандартне відхилення близьке до фактичного необхідно мати вибірку із великою кількістю точок.
Ці ж формули можна застосувати для отримання довірчих інтервалів для дисперсії залишків для методу найменших квадратів, де k тепер буде задавати кількість ступенів свободи для похибки.
Суть стандартного відхилення (приклади)[ред. | ред. код]
Розглянемо наступний приклад, де є дві вибірки даних[4]:
- 1, 2, 3, 4, 5
- -235, -103, 3, 100, 250
З сукупностей очевидно, що вони різні. Якщо порахувати середнє арифметичне, то отримаємо в обох випадках 3. Проте, в другій вибірці дані більше розсіяні довкола центру, а в першому випадку більше сконцентровані в центрі. Тому кажуть, що в другої вибірки велике стандартне відхилення, а в першої незначне. Якщо обчислити дані відхилення, то отримаємо σ1=1,6, а σ2=186. Різниця суттєва.
Здебільшого вибірки не відрізняються настільки, як у попередньому випадку. Наприклад, при проведенні ряду вимірювань отримали дві вибірки[5]:
- x1: 10, 15, 20, 25, 30, 40, 45, 50
- x2: 10, 28, 28, 30, 30, 32, 32, 50
В обох випадках середні значення рівні 30, крім того у них однакові границі. Проте σ1=13,7, а σ2=10,1. Тобто, видно, що при однакових границях і ширині варіації дисперсія і стандартне відхилення виявляються неоднакові: на величини цих показників вплинув різний характер варіювання ознак об'єкта (іншими словами мінливість даних в вибірці).
Стандартне відхилення в ряді випадків виявляється кращим для використання ніж дисперсія, з тієї причини, що воно виражається в тих самих одиницях, що й середня арифметична величина.
Порівняння особливостей розподілу варіант у різних вибірках лише за показниками нормованого відхилення (σ) недостатньо, а іноді неможливе (коли необхідно порівнювати варіаційні ряди, де ознаки вимірювалися в різних одиницях вимірювання, наприклад, одна вибірка — маса людини в кілограмах, а інша — зріст людини в сантиметрах). Для таких порівнянь застосовується відносний показник, який позначається символом t і зветься нормованим відхиленням[6].
Правило 3-х сигм[ред. | ред. код]
Правило 3-х сигм () — практично всі значення нормально розподіленої випадкової величини лежать в інтервалі . Точніше — не менш, ніж із 99,7 % достовірністю, значення нормально розподіленої випадкової величини лежить у вказаному інтервалі (за умови що величина достеменно відома, а не отримана в результаті обробки вибірки). Якщо істинне значення величини невідоме, то слід користуватися не , а . Таким чином правило 3-х сигм перетвориться в правило трьох .
Інтерпретація і застосування[ред. | ред. код]
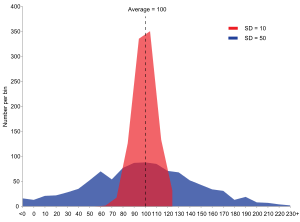

Великі значення стандартного відхилення означають, що точки можуть бути розподілені далеко від середнього, а малі значення стандартного відхилення означають, що точки зосереджені близько до середнього значення вибірки.
Наприклад, кожна із наступних трьох сукупностей {0, 0, 14, 14}, {0, 6, 8, 14} і {6, 6, 8, 8} має середнє значення 7. Їх стандартні відхилення дорівнюють 7, 5, і 1, відповідно. Третя сукупність має набагато менше стандартне відхилення ніж інші дві, оскільки всі її значення знаходяться близько до значення 7. Воно матиме ті самі одиниці вимірювання, що і самі дані вибірки. Якщо, наприклад, вибірка даних {0, 6, 8, 14} представляє вік чотирьох дітей в роках, стандартне відхилення дорівнюватиме 5 рокам. Інший приклад, сукупність {1000, 1006, 1008, 1014} може означати відстань, яку здолали чотири атлети в метрах. Вона має середнє значення в 1007 метрів, і стандартне відхилення в 5 метрів.
Стандартне відхилення може слугувати мірою невизначеності. Наприклад у фізиці, отримане стандартне відхилення серії повторюваних вимірювань визначає точність цих вимірювань. Якщо потрібно вирішити, чи відповідають вимірювання теоретичному передбаченню, стандартне відхилення цих вимірювань має не аби яку важливість: якщо середнє значення вимірювань знаходиться занадто далеко від передбачуваного (де відстань вимірюється як стандартне відхилення), тоді, ймовірно, необхідно переглянути теорію, що перевіряється. Це пояснюється тим, що вони виходять за межі значень, які логічно повинні були очікуватися, якби припущення було вірним і стандартне відхилення визначалося б належним чином.
Хоча стандартне відхилення означає наскільки далеко від середнього можуть бути розподілені дані вимірювань, існують також і інші міри. Наприклад, існує також середнє абсолютне відхилення, яке можна розглядати як більш пряму міру середньої відстані, якщо порівнювати із стандартним відхиленням.
Приклад застосування[ред. | ред. код]
Практичне використання стандартного відхилення для вибірки даних полягає в оцінці величини того, на скільки вони відхиляються від середнього значення.
Експеримент і перевірка гіпотез[ред. | ред. код]
Стандартне відхилення часто використовується для порівняння реальних даних вимірювання із моделлю, з метою її перевірки. Наприклад, в задачах виробництва вага виробів, що виходять із виробничої лінії повинна відповідати встановленому значенню. Зваживши деяку частку виробів можна знайти значення середньої ваги, яка завжди дещо відрізнятиметься від середнього на великій вибірці. Розрахувавши стандартне відхилення, можна отримати мінімальне і максимальне значення в якому середня вага знаходиться із дуже високою ймовірністю (99.9 % або більше). Якщо вона випадає за рамки цих значень, тоді процес виробництва необхідно відлагодити. Статистичні тести подібні до цього є важливими, коли тестування є відносно дорогим. Наприклад, якщо продукт необхідно відкрити, засушити і зважити, або якщо в рамках тесту його необхідно використовувати якимось чином.
В експериментальній науці, застосовують теоретичну модель реальності. У фізиці елементарних часток традиційно використовують стандартне відхилення в «5 сигм» для перевірки відкриття.[7] Це означає, що може існувати один шанс на 3.5 мільйонів що випадкова флуктуація буде відхилятися від результату. Цей рівень правдоподібності необхідно було підтвердити аби мати змогу стверджувати, що частка яка відповідає Бозону Хіггса була відкрита у двох незалежних експериментах в CERN,[8], а також це було мірою впевненості для оголошення про перше виявлення гравітаційних хвиль.[9]
Погода[ред. | ред. код]
В якості простого прикладу можна розглянути середньодобові максимуми температури двох міст, одне з яких знаходиться в прибережній зоні, а друге в глибині суші. Це корисно для розуміння, що діапазон щоденних максимумів температури у містах біля берега є меншим ніж у містах в середині суші. Таким чином, хоч ці два міста можуть мати однакову середню максимальну температуру, стандартне відхилення щоденного максимуму температури для прибережного міста буде меншим ніж у міста в глибині суші, в будь-який обраний день, фактична максимальна температура скоріше за все буде більш відмінною від середньої максимальної температури у місті в глибині суші, на відміну від прибережної зони.
Геометрична інтерпретація[ред. | ред. код]
Аби скласти геометричне уявлення та роз'яснення, розглянемо сукупність із трьох значень, x1, x2, x3. Вони визначають точку P = (x1, x2, x3) в просторі R3. Розглянемо пряму L = {(r, r, r) : r ∈ R}. Це «головна діагональ» що проходить через початок координат. Якщо всі три наші значення є рівними, тоді стандартне відхилення дорівнюватиме нулю і P лежатиме на прямій L. Таким чином можна висунути припущення, що стандартне відхилення пов'язане із відстанню точки P до L. Це дійсно так. Аби виміряти відстань від L ортогонально до точки P, почнемо з точки:
її координати є середніми значеннями, з яких ми почнемо.
| Виведення що |
|---|
|
знаходиться на тому із Пряма буде ортогональною вектору від точки до . Таким чином:
|
Розрахунки показують, що відстань між P і M (що є ортогональною відстанню від P до прямої L) дорівнює стандартному відхиленню вектору x1, x2, x3, помноженому на квадратний корінь від кількості вимірів вектора (в даному випадку це 3.)
Нерівність Чебишова[ред. | ред. код]
Спостереження рідко відхиляється від середнього значення більше ніж на декілька стандартних відхилень. Нерівність Чебишова доводить що, для всіх розподілів, для яких визначено стандартне відхилення, кількість спостережень, що знаходяться в діапазоні, яке відповідає числу стандартних відхилень від середнього значення, буде становити щонайменше таку кількість в процентах, яку вказано в такій таблиці.
| Відстань від середнього | Мінімальна кількість від сукупності |
|---|---|
| 50 % | |
| 2σ | 75 % |
| 3σ | 89 % |
| 4σ | 94 % |
| 5σ | 96 % |
| 6σ | 97 % |
| [10] | |
Правила, що стосуються нормально розподілених величин[ред. | ред. код]
Центральна гранична теорема доводить, що розподіл середнього для багатьох незалежних, однаково розподілених нормальних величин прямує до нормального розподілу із густиною імовірностей, що визначається як
де μ — математичне сподівання випадкових величин, σ дорівнює стандартному відхиленню їх розподілів, розділеному на n1/2, а n — кількість випадкових величин. Таким чином, стандартне відхилення є лише змінною масштабування, яка вказує наскільки широко розтягнутою буде крива розподілу, хоча воно також з'являється і в нормувальній сталій[en].
Якщо розподіл даних є наближеним до нормального, тоді частка даних, які потраплять в діапазон шириною в z стандартних відхилень від середнього задається так:
де — функція помилок. Частка даних, які будуть менше або дорівнюватимуть довільному значенню x, задаються за допомогою кумулятивної функції розподілу імовірностей:
- .[11]
Якщо розподіл даних наближений до нормального, тоді кількість даних, що знаходяться в діапазоні одного стандартного відхилення від середнього значення складатиме 68 процентів від усіх даних (математично цей інтервал описується як μ ± σ, де μ це арифметичне середнє), близько 95 процентів знаходяться в межах двох стандартних відхилень (μ ± 2σ), і близько 99.7 процентів знаходяться в межах трьох стандартних відхилень (μ ± 3σ). Це відомо як правило 68–95–99.7, або емпіричне правило.
Для різних значень z, проценти значень які знаходяться в межах і за межами симетричного інтервалу, CI = (−zσ, zσ), є такими:


| Довірчий інтервал | Частка значень у межах | Частка значень поза межами | |
|---|---|---|---|
| Процент | Процент | Частка | |
| 0.318 639σ | 25 % | 75 % | 3 / 4 |
| 0.674490σ | 50% | 50% | 1 / 2 |
| 0.994458σ | 68 % | 32 % | 1 / 3.125 |
| 1σ | 68.2689492% | 31.7310508% | 1 / 3.1514872 |
| 1.281552σ | 80 % | 20 % | 1 / 5 |
| 1.644854σ | 90 % | 10 % | 1 / 10 |
| 1.959964σ | 95 % | 5 % | 1 / 20 |
| 2σ | 95.4499736% | 4.5500264% | 1 / 21.977895 |
| 2.575829σ | 99 % | 1 % | 1 / 100 |
| 3σ | 99.7300204% | 0.2699796% | 1 / 370.398 |
| 3.290527σ | 99.9 % | 0.1 % | 1 / 1000 |
| 3.890592σ | 99.99 % | 0.01 % | 1 / 10000 |
| 4σ | 99.993666% | 0.006334% | 1 / 15787 |
| 4.417173σ | 99.999 % | 0.001 % | 1 / 100000 |
| 4.5σ | 99.9993204653751% | 0.0006795346249% | 3.4 / 1000000 (з кожного боку від середнього значення) |
| 4.891638σ | 99.9999% | 0.0001% | 1 / 1000000 |
| 5σ | 99.9999426697% | 0.0000573303% | 1 / 1744278 |
| 5.326724σ | 99.99999% | 0.00001% | 1 / 10000000 |
| 5.730729σ | 99.999999% | 0.000001% | 1 / 100000000 |
| 6σ | 99.9999998027% | 0.0000001973% | 1 / 506797346 |
| 6.109410σ | 99.9999999% | 0.0000001% | 1 / 1000000000 |
| 6.466951σ | 99.99999999% | 0.00000001% | 1 / 10000000000 |
| 6.806502σ | 99.999999999% | 0.000000001% | 1 / 100000000000 |
| 7σ | 99.9999999997440% | 0.000000000256% | 1 / 390682215445 |
Див. також[ред. | ред. код]
Джерела[ред. | ред. код]
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Гнеденко Б. В. Курс теории вероятностей. — 6-е изд. — Москва : Наука, 1988. — 446 с.(рос.)
- Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
Посилання[ред. | ред. код]
- ↑ Dodge, Yadolah (2003). The Oxford Dictionary of Statistical Terms. Oxford University Press. ISBN 0-19-920613-9.
- ↑ Pearson, Karl (1894). On the dissection of asymmetrical frequency curves. Philosophical Transactions of the Royal Society A. 185: 71—110. Bibcode:1894RSPTA.185...71P. doi:10.1098/rsta.1894.0003.
- ↑ Miller, Jeff. Earliest Known Uses of Some of the Words of Mathematics.
- ↑ Стандартное отклонение
- ↑ Лакин Г. Ф. Биометрия: Учеб. пособие для биол. спец. вузов. — М: Высш. шк., 1990. — 352 с. — с. 42
- ↑ Калінін М. І., Єлісєєв В. В. Біометрія: Підручник для студентів вузів біологічних і екологічних напрямків. — Миколаїв: Вид-во МФ НаУКМА, 2000. — 204 с. — C. 50-51[недоступне посилання з липня 2019]
- ↑ CERN | Accelerating science. Public.web.cern.ch. Процитовано 10 серпня 2013.
- ↑ CERN experiments observe particle consistent with long-sought Higgs boson | CERN press office. Press.web.cern.ch. 4 липня 2012. Архів оригіналу за 25 березня 2016. Процитовано 30 травня 2015.
- ↑ ((LIGO Scientific Collaboration)), ((Virgo Collaboration)) (2016), Observation of Gravitational Waves from a Binary Black Hole Merger, Physical Review Letters, 116 (6): 061102, arXiv:1602.03837, Bibcode:2016PhRvL.116f1102A, doi:10.1103/PhysRevLett.116.061102, PMID 26918975
- ↑ Ghahramani, Saeed (2000). Fundamentals of Probability (2nd Edition). Prentice Hall: New Jersey. p. 438.
- ↑ Eric W. Weisstein. Distribution Function. MathWorld—A Wolfram Web Resource. Процитовано 30 вересня 2014.
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

![{\displaystyle \operatorname {E} [X]=\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e19f2ee2d8e606b7b96a6667b3e8cd403851b53)

![{\displaystyle {\begin{aligned}\sigma &=+{\sqrt {D}}={\sqrt {\operatorname {E} [(X-\mu )^{2}]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4027e334133a90a48e69787905f011f2a39bf092)










![{\displaystyle [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf)































![{\displaystyle \left[{\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be51cb06ff9be6116d4554e1d44b3d23db610893)
















![{\displaystyle {\text{Proportion}}\leq x={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3907d1b0502235fa3fd00f261b290406a02e7b21)