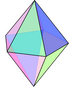
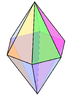
П'ятикутна біпіраміда
П'ятикутна біпіраміда (або дипіраміда) — третє тіло в нескінченному сімействі ізоедральних біпірамід. Кожна біпіраміда є двоїстим многогранником для однорідних призм.
Хоча тіло є ізоедральним, воно не є правильним, оскільки в деяких вершинах сходяться по чотири грані, в інших — по п'ять граней.
Якщо грані є правильними трикутниками, тіло є дельтаедром і многогранником Джонсона (J13, за Залгаллером — 2M3). Тіло можна розглядати як дві п'ятикутні піраміди[en] (J2 = M3), з'єднані основами.
Многогранник Джонсона — це один із 92 строго опуклих многогранників, які мають правильні межі, але не є однорідними (тобто, вони не є правильними многогранниками, архімедовими тілами, призмами або антипризмами).[1].
П'ятикутна біпіраміда є 4-зв'язною, що означає, що потрібно видалити чотири вершини, щоб решта вершин не були зв'язними. Тіло є одним з чотирьох 4-зв'язних симпліційних добре покритих многогранників, що означає, що всі максимальні незалежні множини його вершин мають однаковий розмір. Інші три многогранники з такою властивістю — це правильний октаедр, кирпатий двоклиноїд і неправильний многогранник з 12 вершинами і 20 трикутними гранями[2].

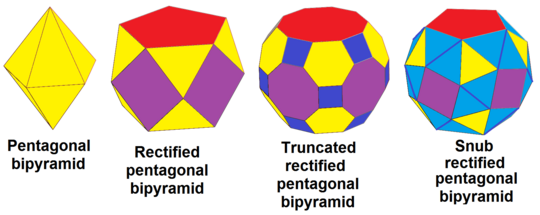
П'ятикутна біпіраміда, dt{2,5}, належить до послідовності зрізань — повне зрізання, rdt{2,5}, зрізання, trdt{2,5} і альтернація[en] (зрізання носів[en]), srdt{2,5}:
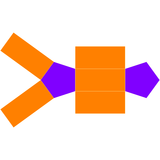
Двоїстий многогранник п'ятикутної піраміди з правильними гранями (тіла Джонсона) — це п'ятикутна призма з 7 гранями — 5 прямокутних граней і 2 п'ятикутники.
| Двоїсте тіло п'ятикутної біпіраміди | Розгортка двоїстого тіла |
|---|---|

|
|
| Багатогранник | 
|

|
|
|

|

|

|

| |
|---|---|---|---|---|---|---|---|---|---|
| Діаграма Коксетера — Динкіна | |||||||||
| Сферична мозаїка | 
|

|

|

|

|

|

|

|

|
| Конфігурація грані | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
- ↑ Johnson, 1966, с. 169—200.
- ↑ Finbow, Hartnell, Nowakowski, Plummer, 2010, с. 894–912.
- Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158, вип. 8 (31 жовтня). — С. 894–912. — DOI:.
- Norman W. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18 (31 жовтня). — С. 169–200. — DOI:.
- Weisstein, Eric W. Pentagonal dipyramid(англ.) на сайті Wolfram MathWorld.
- Нотація Конвея для многогранників Ввести: dP5