Маса
| Маса | ||||
|
Міжнародний еталон кілограма, зроблений у вигляді циліндра, з діаметром і висотою 39,17 мм. Матеріал — сплав з вмістом 90 % платини та 10 % іридію. Еталон зберігається у штаб-квартирі Міжнародного бюро мір і ваг у Севрі | ||||
| Символи: | m | |||
|---|---|---|---|---|
| Одиниці вимірювання | ||||
| SI | кілограм (кг) | |||
| СГС | грам (г) | |||
| Інші одиниці | інерта (МКГСС), тонна (МТС) | |||
| Розмірність: | M | |||
|
| ||||
| Класична механіка |
|---|
| Історія класичної механіки |
|
Фундаментальні поняття Простір · Час · Система відліку · Маса · Інерція · Швидкість · Прискорення · Імпульс · Сила · Гравітація · Момент імпульсу · Момент сили · Момент інерції · Енергія · Кінетична енергія · Потенціальна енергія · Механічна робота · Потужність |
|
Основні принципи |
|
Важливі теми |
|
Формулювання |
Ма́са — основна фізична величина, яка вважається однією з фундаментальних характеристик матерії, що визначає її інерційні, енергетичні та гравітаційні властивості від макроскопічних об'єктів до атомів і елементарних частинок. У сучасній фізиці елементарних частинок, яка ґрунтується на квантовій теорії поля, вважається, що маса не є фундаментальною властивістю частинок матерії, а набувається шляхом взаємодії частинок зі спеціальним полем Хіггса.
Маса є скалярною величиною та зазвичай позначається латинською літерою m.
Одиниці вимірювання маси[ред. | ред. код]
Одиницею вимірювання маси в системі SI є кілограм, скорочено позначається малими літерами кг, міжнародне позначення kg[1]. За визначенням , прийнятим III Генеральною конференцією з мір і ваг (ГКМВ) у 1901 році[2], до 2018 року: «Один кілограм є одиницею маси, що дорівнює масі міжнародного прототипу кілограма». Однак це визначення є застарілим, оскільки за станом на 2021 рік всі основні одиниці системи SI визначаються через фізичні константи.
Чинне визначення (2018 р.)[3][4]:
|
кілограм визначається через сталу Планка h, яка точно дорівнює 6.62607015×10−34 Дж⋅с (Дж = кг⋅м2⋅с−2), та визначення метра і секунди. |
У системі СГС й Гаусовій системі у тому числі, маса вимірюється в грамах (1⁄1000 кілограма). В атомній фізиці заведено прирівнювати масу до атомної одиниці маси, у фізиці твердого тіла — до маси електрона, у фізиці елементарних частинок масу вимірюють в електронвольтах.
Крім цих одиниць, що використовуються в науці, існує велика різноманітність історичних одиниць маси, які зберегли свою окрему сферу використання: фунт, унція, карат, тонна тощо. В астрономії одиницею для порівняння мас небесних тіл слугує маса Сонця.
У деяких природних системах одиниць як одиницю маси використовують маси елементарних частинок: електрона чи протона[5]. У системі одиниць Планка, що також належить до природних систем, одиницею маси є планківська маса.
Маси дуже дрібних частинок можуть бути визначені за допомогою величини, оберненої до комптонівської довжини хвилі: 1 см-1 ≈ 3.52×10−41 кг. Маса дуже великої зорі або чорної діри може ототожнюватись з її гравітаційним радіусом: 1 см ≈ 6.73×1024 кг.
Історичний нарис[ред. | ред. код]
Слово маса (лат. massa, від дав.-гр. μαζα) на початках в античні часи означало шматок тіста. Згодом зміст слова розширився, і воно стало означати цільний, необроблений шматок довільної речовини; у цьому сенсі слово вживається, наприклад, у Овідія та Плінія[6].
Поняття маси як наукового терміну було введено у фізику Ньютоном, до цього дослідники оперували тільки поняттям ваги. У праці «Математичні начала натуральної філософії» Ньютон спочатку визначив «кількість матерії» у фізичному тілі як добуток його густини на об'єм. Далі він вказав, що в тому ж розумінні буде використовувати термін маса. Нарешті, Ньютон вводить поняття маси у закони фізики: спочатку у другий закон Ньютона (через кількість руху), а потім — у закон всесвітнього тяжіння, звідки відразу випливає, що вага пропорційна масі.
У ньютонівській механіці маса — величина додатна й адитивна, тобто маса m будь-якої системи матеріальних точок (наприклад, твердого тіла) дорівнює сумі мас усіх n точок цієї системи:
- .
Крім цього, в ньютонівській механіці вважається, що:
- маса тіла не залежить ні від стану його руху, ні від місцезнаходження тіла в просторі, ні від того, діють на нього інші тіла чи ні;
- справджується закон збереження маси: маса механічної системи не змінюється з часом, якщо не відбувається обмін речовиною між системою і зовнішніми тілами (зовнішнім середовищем).
Фактично Ньютон використовує тільки два розуміння маси: як міри інертності і джерела тяжіння. Тлумачення її як міри «кількості матерії» — не більш ніж наочна ілюстрація, і воно зазнало критики ще в XIX столітті як нефізичне та беззмістовне.
Тривалий час одним з головних законів природи вважався закон збереження маси. Однак у XX столітті з'ясувалося, що цей закон є окремим випадком закону збереження енергії, і в деяких ситуаціях (ядерні реакції, релятивістська механіка тощо) не виконується.
Види маси[ред. | ред. код]
Існує дві різні величини, які мають спільну назву «маса»:
- Інертна маса характеризує здатність тіла чинити опір зміні стану його руху під дією сили. За умови, що сила однакова, об'єкт з меншою масою легше змінює стан руху ніж об'єкт з більшою масою. Інертна маса фігурує у спрощеній формі другого закону Ньютона, а також у формулі для визначення імпульсу тіла у класичній механіці.
- Гравітаційна маса характеризує інтенсивність взаємодії тіла з гравітаційним полем. Вона фігурує у Ньютонівському законі всесвітнього тяжіння.
Перша перевірка пропорційності двох видів маси була зроблена Галілеєм, який вивчав вільне падіння. Згідно з дослідами Галілея, усі тіла, незалежно від їх маси і матеріалу, падають з однаковим прискоренням. Зараз ці досліди можна трактувати так, що збільшення сили, що діє на масивніше тіло з боку гравітаційного поля Землі, повністю компенсується збільшенням його інертних властивостей. Пізніше на пропорційність інертної і гравітаційної мас звернув увагу Ньютон, він же вперше довів, що ця пропорційність витримується з точністю не меншою за 0,1 %[7].
Хоча інертна маса і гравітаційна маса є концептуально різними поняттями, всі відомі на сьогоднішній день експерименти свідчать, що ці маси пропорційні між собою. Пропорційність (умовно кажучи, «рівність мас») експериментально перевірено з дуже високою точністю: чутливість до відносної різниці у найкращому експерименті на 2009 рік[8] має порядок 10−13. Такого роду експерименти привели до формулювання принципу еквівалентності сил інерції та гравітації:
Усі явища в гравітаційному полі відбуваються так само, як у відповідному полі сил інерції, якщо є однаковими напруженості цих полів та однакові початкові умови для тіл системи.
Це дозволяє побудувати систему одиниць так, щоб одиниця вимірювання мас була одна й та сама, і вони були рівні між собою. Практично всі системи одиниць побудовані за цим принципом.
У загальній теорії відносності інертна та гравітаційна маси вважаються повністю еквівалентними.
Рівняння[ред. | ред. код]
Як міра інертності тіла, маса входить до другого закону Ньютона, записаного у спрощеному (для випадку сталої маси) вигляді
- ,
де — прискорення, а — сила, що діє на тіло.
Маса входить також у квантові рівняння руху: рівняння Шредінгера, рівняння Дірака тощо.
Як величина, що визначає гравітаційну взаємодію тіл, маса входить до формулювання закону всесвітнього тяжіння
- ,
де G — гравітаційна стала, і — маси двох тіл (матеріальних точок), що взаємодіють одне з одним, — сила, яка діє з боку другого тіла на перше, — вектор, проведений від першого тіла до другого. Це можна інтерпретувати таким чином, що маса визначає величину гравітаційного поля, створеного другим тілом, а маса силу, з якою це поле діє на перше тіло. Закон всесвітнього тяжіння є симетричним стосовно мас тіл. У наведеному вигляді його можна використовувати не тільки для матеріальних точок, але і для сферичних тіл, відстань між якими перевищує суму їхніх радіусів.
Зв'язок із енергією[ред. | ред. код]
Маса є інваріантною величиною-скаляром — модулем 4-вектора енергії-імпульсу. Тобто, енергія та компоненти імпульсу як, відповідно, часова та просторові компоненти 4-вектора енергії-імпульсу змінюються через перетворення Лоренца при переході до іншої інерціальної системи відліку, а маса залишається сталою:
- [9].
Відповідно до цього, маса може бути еквівалентом лише енергії спокою.
Закони збереження[ред. | ред. код]
У 18 столітті хімічні досліди встановили закон збереження маси при хімічних перетвореннях. Сумарна маса речовин, які вступають у хімічну реакцію, дорівнює сумарній масі речовин, що утворюються в результаті реакції. Однак у релятивістській фізиці закон збереження маси не діє.
Маса елементарних частинок[ред. | ред. код]
Маса, точніше маса спокою, є важливою характеристикою елементарних частинок. Питання про те, якими причинами зумовлені ті значення маси частинок, які спостерігаються на досліді, є важливою проблемою фізики елементарних частинок. Так, наприклад, маса нейтрона дещо більша за масу протона, що зумовлено різницею у взаємодії кварків, із яких складаються ці частинки. Приблизна однаковість мас деяких частинок дозволяє об'єднувати їх у групи, трактуючи як різні стани одної загальної частинки із різними значеннями ізотопічного спіну.
Узагальнення поняття маси[ред. | ред. код]
При малих значеннях імпульсу вільної частинки, тобто такої, на яку не діють жодні сили, енергія частинки визначається формулою
- ,
де p — імпульс частинки. Така залежність енергії від імпульсу називається параболічним законом дисперсії.
В багатьох випадках залежність енергії складнішої фізичної системи від маси має аналогічний квадратичний вид. Наприклад, така залежність властива для закону дисперсії енергетичних зон у твердому тілі. Для таких систем можна ввести аналогічну масі величину, яку називають ефективною масою.
Інваріантна маса[ред. | ред. код]
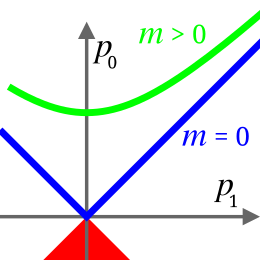
Одне з узагальнень маси із класичної фізики; в сучасних працях по теорії відносності, ядерній фізиці, фізиці елементарних часток і т. і. звичайно просто «масою» і називається. Домінує точка зору, що терміни «маса спокою» та «релятивістська маса» є застарілими[10]. ; перший мусить бути замінений на термін «маса», а другий взагалі має бути відкинутий, оскільки може привести до помилкових суджень.
В спеціальній теорії відносності фізична величина швидкість використовується як проміжна величина, котра входить в функцію Лагранжа. Проте в теоретичній фізиці використовується гамільтонова форма рівнянь руху, котра є найбільш прийнятна для використання в квантовій механіці та електродинаміці. В рамках підходу Ландау-Ліфшіца взаємозв'язок між швидкістю та імпульсом має вигляд:
- ,
тоді як квадрат модуля є:
- .
Із цих двох рівнянь можна знайти основне співвідношення, котре зв'язує масу, імпульс та енергію частинки:
- .
Очевидно, що при (), ми будемо мати т.з. енергію спокою:
- .
Тут слід відзначити, що використовується термін енергія спокою, а не «маса спокою».
Кожна з відомих елементарних частинок має строго визначену масу спокою, яка є її базовою характеристикою. Існує чимало різних теорій, які намагаються пояснити, чому та чи інша частинка має саме таку масу спокою.
Існують частинки, які не мають маси спокою. Такі частинки завжди рухаються зі швидкістю світла. Природно, що до таких часток належать кванти світла — фотони.
Питання про те, чи має масу спокою нейтрино тісно зв'язане із проблемою темної речовини у Всесвіті та із сценаріями еволюції Всесвіту і є однією із найцікавіших загадок фізики.
Вимірювання маси[ред. | ред. код]
Методи та засоби для вимірювання[ред. | ред. код]



Більшість приладів для вимірювання маси ґрунтується на використанні принципу еквівалентності інертної і гравітаційної маси. За допомогою таких приладів, що їх називають «вагами», масу тіл визначають за їхньою вагою. В пружинних вагах вага вимірюється за ступенем деформації пружини. У важільних — вага визначається через порівняння ваги об'єкту зважування з вагою еталонів (гир) відомої маси.
Однак, у стані невагомості (скажімо, на космічних станціях) такі ваги незастосовні й використовуються інші пристрої — вимірювачі маси тіла в невагомості (масметри), дія яких ґрунтується на вимірюванні періоду вільних коливань вантажу на пружині; цей період, як відомо, залежить від маси тіла.
Маси заряджених елементарних частинок визначають за їхніми слідами у камері Вільсона[11]. Маси короткоживучих елементарних частинок, що не залишають слідів в камері Вільсона, визначають, оцінюючи сумарну енергію продуктів їх розпаду[12][13].
Масу Землі визначають на основі закону всесвітнього тяжіння Ньютона, виходячи з відомих значень гравітаційної сталої та радіуса Землі[14]. Масу Сонця визначають також на основі закону всесвітнього тяжіння Ньютона, виходячи з відомих значень гравітаційної сталої, відстані між Землею та Сонцем й періоду обертання Землі навколо Сонця[15]. Маса нашої Галактики визначається, виходячи з періоду обертання околиць Сонця навколо центра Галактики та відстані до центра Галактики[16].
Маси найближчих подвійних зірок визначаються за відстанями між ними та періодом їхнього обертання. Якщо зірка не має супутника і належить до головної послідовності, то її масу можна визначити, виходячи з її світності або температури поверхні[17].
Значення мас різних об'єктів[ред. | ред. код]
| Маса (кг) | в інших одиницях | ||
| Електрон | еВ | ||
| Протон | еВ | ||
| Бозон Хіггса | еВ | ||
| Вірус грипу | |||
| Сніжинка | |||
| Тіло людини | кілограмів | ||
| Слон | тонн | ||
| Кит | тонн | ||
| Піраміда Хеопса | тонн | ||
| Земля | мас Землі | ||
| Юпітер | мас Землі | ||
| Сонце | мас Сонця | ||
| Інші зорі | мас Сонця | ||
| Наша Галактика | мас Сонця | ||
| Інші галактики | мас Сонця |
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ ДСТУ 3651.0-97 Метрологія. Одиниці фізичних величин Основні одиниці фізичних величин міжнародної системи одиниць Основні положення, назви та позначення.
- ↑ Unit of mass (kilogram). SI Brochure: The International System of Units (SI) [8th edition, 2006; updated in 2014] (англ.). BIPM. Архів оригіналу за 2 січня 2021. Процитовано 11 листопада 2015.
- ↑ Mirandés, Estefanía de; Barat, Pauline; Stock, Michael; Milton, Martin J. T. (2016). Calibration campaign against the international prototype of the kilogram in anticipation of the redefinition of the kilogram, part II: evolution of the BIPM as-maintained mass unit from the 3rd periodic verification to 2014. Metrologia (англ.). Т. 53, № 5. с. 1204. doi:10.1088/0026-1394/53/5/1204. ISSN 0026-1394. Процитовано 16 листопада 2018.
- ↑ Weule, Genelle (16 листопада 2018). If you thought a kilogram weighed a kilogram, you were wrong (and the definition is about to change). ABC News (en-AU) . Архів оригіналу за 17 листопада 2018. Процитовано 16 листопада 2018.
- ↑ Tomilin K. A. (1999-06). Natural Systems of Units: To the Centenary Anniversary of the Planck System (PDF). Proc. of the XXII Internat. Workshop on high energy physics and field theory (англ.). Архів оригіналу (PDF) за 12 травня 2016. Процитовано 22 грудня 2016.
- ↑ Джеммер, М., 1967, Глава I.
- ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5.
- ↑ S. Schlamminger, K.-Y. Choi, T. A. Wagner, J. H. Gundlach, and E. G. Adelberger Test of the Equivalence Principle Using a Rotating Torsion Balance // Phys. Rev. Lett. 100, 041101 (2008). Published 28 January 2008
- ↑ 4-імпульс
- ↑ Л. Б. Окунь, Успехи физических наук, 2000, т. 170, с. 1366 [1]
- ↑ Завельский, 1970, с. 119.
- ↑ Завельский, 1970, с. 123.
- ↑ Копылов Г. И. Всего лишь кинематика. — М. : Атомиздат, 1968. — 176 с.
- ↑ Завельский, 1970, с. 136.
- ↑ Завельский, 1970, с. 150.
- ↑ Завельский, 1970, с. 161.
- ↑ Киппенхан Р. 100 миллиардов солнц. Рождение, жизнь и смерть звезд. — М.: Мир, 1990. — С. 281—284 — ISBN 5-03-001195-1.
Література[ред. | ред. код]
- Кучерук І. М., Горбачук І. Т., Луцик П. П. Загальний курс фізики : навч. посібник у 3-х т. — Київ : Техніка, 2006. — Т. 2 : Електрика і магнетизм.
- Єжов С. М., Макарець М. В., Романенко О. В. Класична механіка. — К. : ВПЦ "Київський університет", 2008. — 480 с.
- Сук О. П., Базакуца В. А. Фізичні величини та одиниці. — Х. : ХДПУ, 1998. — 320 с.
- Федорченко А. М. Теоретична механіка. — К. : Вища школа, 1975. — 516 с.
- Ландау Л. Д., Лифшиц Е. М. Теория поля // Теоретическая физика. — М. : Физматлит, 2006. — Т. 2. — 536 с.
- Завельский Ф. С. Взвешивание миров, атомов и элементарных частиц. — М. : Атомиздат, 1970. — 176 с.
- Макс Джеммер. Понятие массы в классической и современной физике. — М. : Прогресс, 1967. — 254 с.
- Яворський Б. М., Детлаф А. А., Лебедев А. К. Довідник з фізики для інженерів та студентів вищих навчальних закладів / Переклад з 8-го переробл. і випр. вид. — Т. : Навчальна книга — Богдан, 2007. — 1040 с. — ISBN 966-692-818-3.
Посилання[ред. | ред. код]
- Francisco Flores (6 лютого 2012). The Equivalence of Mass and Energy. Stanford Encyclopedia of Philosophy. Архів оригіналу за 8 травня 2021. Процитовано 3 грудня 2013. (англ.)
- Gordon Kane (27 червня 2005). The Mysteries of Mass (PDF). Scientific American. Архів оригіналу (PDF) за 12 серпня 2017. Процитовано 3 грудня 2013. (англ.)
- L. B. Okun (15 листопада 2001). Photons, Clocks, Gravity and the Concept of Mass (PDF). Nuclear Physics. Архів оригіналу (PDF) за 29 вересня 2013. Процитовано 3 грудня 2013. (англ.)
- Frank Wilczek (20 липня 2007). The Origin of Mass (video). MIT Video. Архів оригіналу за 8 травня 2017. Процитовано 33 серпня 2018. (англ.)
- John Baez[en] та ін. (2012). What is relativistic mass?. Архів оригіналу за 30 червня 2007. Процитовано 3 грудня 2013. (англ.)
- John Baez[en] та ін. (2008). What is the mass of a photon?. Архів оригіналу за 31 травня 2014. Процитовано 3 грудня 2013. (англ.)
- David R. Williams (12 лютого 2008). The Apollo 15 Hammer-Feather Drop. NASA. Архів оригіналу за 8 травня 2021. Процитовано 3 грудня 2013. (англ.)
|











































