Прискорення
Матеріал з Вікіпедії — вільної енциклопедії.
Приско́ренням називається зміна швидкості тіла за одиницю часу. Математично прискорення описується як похідна швидкості за часом.
Прискорення позначається зазвичай латинською літерою a й в скалярному випадку вимірюється в системі СІ в метрах за секунду в квадараті (м/с2). В системі СГС одиниця вимірювання прискорення сантиметр за секунду в квадраті (см/с2). Часто прискорення також вимірюють, вибираючи за одиницю прискорення вільного падіння, тобто говорять, що прискорення складає, наприклад, 2g.
Оскільки швидкість - похідна від координати, то прискорення можна записати, як другу похідну від координати.
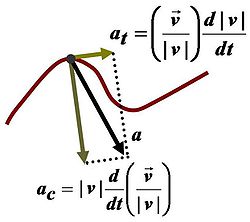
Прискорення векторна величина. Його напрямок не завжди співпадає із напрямком швидкості. У випадку обертання прискорення перпендикулярне до швидкості. В загальному випадку вектор прискорення можна розкласти на дві складові. Складова вектора прискорення, яка направлена паралалельно до вектора швидкості, а, отже, вздовж дотичної до траєкторії називається тангенціальним прискоренням. Складова вектора прискорення, що направлена перпендикулярно до вектора швидкості, а, отже, вздовж нормалі до траєкторії, називається нормальним прискоренням.
Рух тіла, при якому прискорення не змінюєтья ні за величиною ні за напрямком називаєтсья рівноприскореним рухом.
Зміст |
[ред.] Прискорення тіла, що рухається по колу
Якщо тіло рухається по колу із сталою кутовою швидкістю ω, то його прискорення спрямоване до центра кола й дорівнює за абсолютною величиною
,
де R - радіус кола, v = ωR - швидкість тіла.
[ред.] 4-вектор прискорення
В теорії відносності рух із змінною швидкістю теж характеризується певною величиною, аналогічною прискоренню, але на відміну від звичайного прискорення 4-вектор прискорення є другою похідною від 4-вектора координат не по часу, а по просторово-часовому інтервалу.
.
4-вектор прискорення завжди "перпендикулярний" 4-швидкості
.
 |
Це незавершена стаття з фізики. Ви можете допомогти проекту, виправивши або дописавши її. |
[ред.] Цікаві факти
Максимальне прискорення твердого тіла, яке вдалося отримати в лабораторних умовах, складало 1010g.[1] Для досліду вчені застосували так звану Z-машину (Z Machine), яка створює надзвичайно потужний імпульс магнітного поля, який прискорює в спеціальному каналі снаряд – алюмінієву пластинку розміром 30×15 мм і товщиною 0,85 мм. Швидкість снаряда становила приблизно 34 км/с (у 50 раз швидше за кулю).
[ред.] Дивіться також
[ред.] Посилання
[ред.] Джерела
- Федорченко А.М.. Теоретична механіка (1975), Київ: Вища школа., 516 с.
