Адвекція

Адвекція — термін, що застосовується у фізиці, інженерії та науках про Землю для опису перенесення речовини в потоках як цілого.
Загальний опис[ред. | ред. код]
У хімії атмосфери — переміщення повітря, його властивостей (таких як тепло), розпорошених у ньому речовин, туману і т. ін. лише шляхом переважно горизонтального руху атмосферних мас.
Речовина переноситься разом з усіма своїми властивостями. Здебільшого через адвекцію відбувається перенесення рідин. Властивості, які переносяться з речовиною зберігаються наприклад енергія. Прикладом адвекції є перенесення бруду та мулу в річках водним потоком вниз за течією. Переносити матеріали у своєму потоці може будь-яка речовина, що має теплову енергію, наприклад вода або повітря.
Під час атвекції рідини переносять деякі частинки як ціле в потоці. Рух рідини описується математично векторним полем, а матеріал, що переноситься, — скалярним полем, яке задає його розподіл у просторі. Адвекція вимагає потоків рідини, а тому не може відбуватися у твердих тілах. Вона не включає перенесення речовин через так звану молекулярну дифузію.
Адвекцію іноді плутають з більш загальним поняттям конвекції, що включає як адвективний, так і дифузійний перенесення.
У метеорології і фізичній океанографії адвекція часто належить до поширення деяких властивостей атмосфери та океану, таких як тепло, вологість (див. вологість) або солоність. Адвекція важлива для формування орографічних хмар і опадів, як частин гідрологічного циклу.
Різниця між адвекцію і конвекцією[ред. | ред. код]
Термін адвекції іноді виступає як синонім для конвекції, але технічно, конвекція покриває два поняття дифузії і адвекції. Адвекція описує рух деякої кількості речовини через об'ємний переріз рідини (річка або трубопровод).[1][2]
Метеорологія[ред. | ред. код]
У метеорології і фізичній океанографії адвекція часто описує горизонтальне транспортування деяких властивостей атмосфери або океану, наприклад, спеки, вологості або солоності. Конвекція, як правило, належить до вертикального руху (вертикальної адвекції). Адвекція важлива для формування орографічних хмар і опадів, як частин гідрологічного циклу.
Математика адвекції[ред. | ред. код]
Рівняння адвекції це диференціальне рівняння в частинних похідних, яке регулює рух, зберігання скалярного поля, вектор швидкості поля. Воно бере до уваги скалярне поле, закон збереження, разом з теоремою Гаусса.
Легко візуалізується, приклад адвекції як транспортування чорнила в річці. Чорнило буде рухатися вниз за течією в «пульс» через адвекцію. При додаванні в озеро, без істотних масових витрат води, чорнило буде просто розходитися назовні дифузійним чином, що не є адвекцією. Зверніть увагу, що, якщо воно рухається вниз за течією, «пульс» чорнила також буде поширюватися через дифузію. Сукупність цих процесів називається конвекцією.
Рівняння адвекції[ред. | ред. код]
В Декартових координатах оператор адвекції
- .
де це поле швидкостей, і - оператор дивергенції (зверніть увагу, що тут використовуються Декартові координати).
У рівнянні адвекції постійною величиною описується скалярне поле і виражається математично через рівняння нерозривності:
де це оператор дивергенції і це швидкість векторного поля. Часто передбачається, що потік є нестисливий, тобто поле швидкостей задовольняє рівняння
і називається соленоїдним. Якщо це так, вищенаведене рівняння може бути переписано як
Зокрема, якщо потік стійкий, то
який показує, що є сталою вздовж оптимізації. Отже, і не змінюються в часі.
Якщо векторна величина (наприклад, магнітне поле) буде переноситься на соленоїднім полі швидкості вищевказане рівняння адвекції стає:
Тут це векторне поле замість скалярного поля .
Розв'язання рівняння[ред. | ред. код]
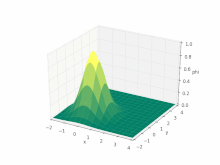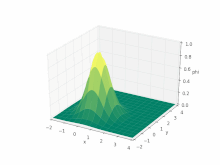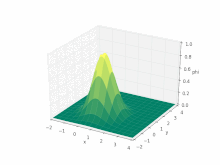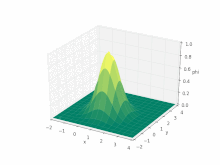
Рівняння адвекції непросто розв'язати чисельно: система є гіперболічним диференціальним рівнянням у частинних похідних.
Навіть для одновимірного руху та постійного поля швидкості, система, як і раніше, залишається практично нерозв'язною. Рівняння набуває вигляду
де — скалярне поле, а — -ва компонента вектора .
Див. також[ред. | ред. код]
- Рівняння збереження
- Конвекція
- Число Куранта
- Число Пекле
- Перерегулювання (сигнал)
- Дель
- Атмосфера землі
- Дифузія
- Випромінювання
Джерела[ред. | ред. код]
Посилання[ред. | ред. код]
- Адвекція [Архівовано 29 вересня 2020 у Wayback Machine.] // ВУЕ
- Дисертація числове моделювання нелінійних еволюційних задач Дифузії-Адвеції-Реакції[недоступне посилання з листопадаа 2019] (Львівський національний університет імені Івана Франка, Факультет прикладної математики та інформатики автор: Вовк Олександр Володиммрович)
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

















