Інтерполяція Ерміта. Кубічні сплайни Ерміта — кубічні сплайни , що використовують інтерполювання поліномами методом Ерміта. Цей метод інтерполювання використовує дві контрольні точки та два вектори напрямків.
Названі на честь французького математика Шарля Ерміта .
Кубічні поліноміальні сплайни широко використовуються у галузі комп'ютерної графіки та геометричного моделювання для отримання кривих або траєкторії руху, що проходять через задані точки площини або тривимірного простору .
Інтерполяція на інтервалі Інтерполяція на інтервалі (0,1)
f(t)
f(0)
f(1)
f'(0)
f'(1)
h
00
(
t
)
{\displaystyle \ h_{00}(t)}
1
0
0
0
h
01
(
t
)
{\displaystyle \ h_{01}(t)}
0
1
0
0
h
10
(
t
)
{\displaystyle \ h_{10}(t)}
0
0
1
0
h
11
(
t
)
{\displaystyle \ h_{11}(t)}
0
0
0
1
p
(
t
)
{\displaystyle \mathbf {p} (t)}
p
0
{\displaystyle \mathbf {p_{0}} }
p
1
{\displaystyle \mathbf {p_{1}} }
m
0
{\displaystyle \mathbf {m_{0}} }
m
1
{\displaystyle \mathbf {m_{1}} }
Задано початкову точку
p
0
{\displaystyle p_{0}}
m
0
{\displaystyle m_{0}}
t
=
0
{\displaystyle t=0}
p
1
{\displaystyle p_{1}}
m
1
{\displaystyle m_{1}}
t
=
1
{\displaystyle t=1}
Для кубічного полінома та його похідної
p
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
{\displaystyle \mathbf {p} (t)=a_{0}+a_{1}t+a_{2}t^{2}+a_{3}t^{3}}
p
′
(
t
)
=
a
1
+
2
a
2
t
+
3
a
3
t
2
{\displaystyle \mathbf {p} \prime (t)=a_{1}+2a_{2}t+3a_{3}t^{2}}
виразимо коефіцієнти
a
0
,
a
1
,
a
2
,
a
3
{\displaystyle a_{0},a_{1},a_{2},a_{3}}
p
(
0
)
,
p
(
1
)
,
p
′
(
0
)
,
p
′
(
1
)
{\displaystyle \mathbf {p} (0),\mathbf {p} (1),\mathbf {p} \prime (0),\mathbf {p} \prime (1)}
{
p
(
0
)
=
a
0
p
(
1
)
=
a
0
+
a
1
+
a
2
+
a
3
p
′
(
0
)
=
a
1
p
′
(
1
)
=
a
1
+
2
a
2
+
3
a
3
⇒
{
a
0
=
p
(
0
)
a
1
=
p
′
(
0
)
a
2
=
3
(
p
(
1
)
−
p
(
0
)
)
−
2
p
′
(
0
)
−
p
′
(
1
)
a
3
=
p
′
(
0
)
+
p
′
(
1
)
−
2
(
p
(
1
)
−
p
(
0
)
)
{\displaystyle {\begin{cases}\mathbf {p} (0)=a_{0}\\\mathbf {p} (1)=a_{0}+a_{1}+a_{2}+a_{3}\\\mathbf {p} \prime (0)=a_{1}\\\mathbf {p} \prime (1)=a_{1}+2a_{2}+3a_{3}\end{cases}}\Rightarrow {\begin{cases}a_{0}=\mathbf {p} (0)\\a_{1}=\mathbf {p} \prime (0)\\a_{2}=3(\mathbf {p} (1)-\mathbf {p} (0))-2\mathbf {p} \prime (0)-\mathbf {p} \prime (1)\\a_{3}=\mathbf {p} \prime (0)+\mathbf {p} \prime (1)-2(\mathbf {p} (1)-\mathbf {p} (0))\end{cases}}}
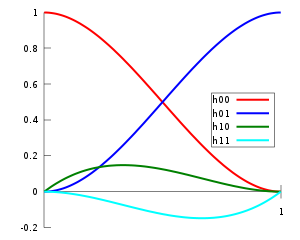
Підставивши значення полінома та його похідної із таблиці справа, отримаємо чотири базові ермітові поліноми:
Базис для кубічних ермітових сплайнів.
h
00
(
t
)
=
2
t
3
−
3
t
2
+
1
=
(
1
−
t
)
2
(
1
+
2
t
)
h
01
(
t
)
=
−
2
t
3
+
3
t
2
=
t
2
(
3
−
2
t
)
h
10
(
t
)
=
t
3
−
2
t
2
+
t
=
t
(
1
−
t
)
2
h
11
(
t
)
=
t
3
−
t
2
=
t
2
(
t
−
1
)
{\displaystyle {\begin{matrix}h_{00}(t)&=&2t^{3}-3t^{2}+1&=&(1-t)^{2}(1+2t)\\h_{01}(t)&=&-2t^{3}+3t^{2}&=&t^{2}(3-2t)\\h_{10}(t)&=&t^{3}-2t^{2}+t&=&t(1-t)^{2}\\h_{11}(t)&=&t^{3}-t^{2}&=&t^{2}(t-1)\\\end{matrix}}}
Тоді інтерполяційний поліном визначається як лінійна комбінація чотирьох базових:
p
(
t
)
=
h
00
(
t
)
p
0
+
h
10
(
t
)
m
0
+
h
01
(
t
)
p
1
+
h
11
(
t
)
m
1
,
t
∈
[
0
,
1
]
{\displaystyle \mathbf {p} (t)=h_{00}(t)\mathbf {p_{0}} +h_{10}(t)\mathbf {m_{0}} +h_{01}(t)\mathbf {p_{1}} +h_{11}(t)\mathbf {m_{1}} ,\qquad t\in [0,1]}
Існують такі властивості симетрії:
h
00
(
t
)
+
h
01
(
t
)
=
1
{\displaystyle \ h_{00}(t)+h_{01}(t)=1}
h
00
(
t
)
=
h
01
(
1
−
t
)
{\displaystyle \ h_{00}(t)=h_{01}(1-t)}
h
10
(
t
)
=
−
h
11
(
1
−
t
)
{\displaystyle \ h_{10}(t)=-h_{11}(1-t)}
Інтерполяція на інтервалі
(
x
k
,
x
k
+
1
)
{\displaystyle (x_{k}\,,\;x_{k+1})}
Інтерполяція на цьому інтервалі задається формулою
p
(
x
)
=
h
00
(
t
)
p
0
+
h
10
(
t
)
h
m
0
+
h
01
(
t
)
p
1
+
h
11
(
t
)
h
m
1
,
h
=
x
k
+
1
−
x
k
,
t
=
(
x
−
x
k
)
/
h
.
{\displaystyle \mathbf {p} (x)=h_{00}(t)\mathbf {p_{0}} +h_{10}(t)h\mathbf {m_{0}} +h_{01}(t)\mathbf {p_{1}} +h_{11}(t)h\mathbf {m_{1}} ,\qquad h=x_{k+1}-x_{k},\qquad t=(x-x_{k})/h.}
Зв'язок з кривими Без'є Чотири базові ермітові поліноми легко виразити через поліноми Бернштейна , що є базисними для кривих Без'є
h
00
(
t
)
=
(
1
−
t
)
2
(
1
+
2
t
)
=
(
1
−
t
)
3
+
3
t
(
1
−
t
)
2
=
b
0
,
3
(
t
)
+
b
1
,
3
(
t
)
h
01
(
t
)
=
t
2
(
3
−
2
t
)
=
t
3
+
3
t
2
(
1
−
t
)
=
b
3
,
3
(
t
)
+
b
2
,
3
(
t
)
h
10
(
t
)
=
t
(
1
−
t
)
2
=
b
1
,
3
(
t
)
/
3
h
11
(
t
)
=
t
2
(
t
−
1
)
=
−
b
2
,
3
(
t
)
/
3
{\displaystyle {\begin{matrix}h_{00}(t)&=&(1-t)^{2}(1+2t)&=&(1-t)^{3}+3t(1-t)^{2}&=&\mathbf {b} _{0,3}(t)+\mathbf {b} _{1,3}(t)\\h_{01}(t)&=&t^{2}(3-2t)&=&t^{3}+3t^{2}(1-t)&=&\mathbf {b} _{3,3}(t)+\mathbf {b} _{2,3}(t)\\h_{10}(t)&=&t(1-t)^{2}&=&&&\mathbf {b} _{1,3}(t)/3\\h_{11}(t)&=&t^{2}(t-1)&=&&&-\mathbf {b} _{2,3}(t)/3\\\end{matrix}}}
Тому кубічний сплайн Ерміта з параметрами
(
p
0
,
p
1
,
m
0
,
m
1
)
{\displaystyle \mathbf {\left(p_{0},p_{1},m_{0},m_{1}\right)} }
аналогічний кубічній кривій Без'є з опорними вершинами
(
p
0
,
p
1
,
p
0
+
m
0
3
,
p
1
−
m
1
3
)
.
{\displaystyle \mathbf {\left(p_{0},p_{1},p_{0}+{\frac {m_{0}}{3}},p_{1}-{\frac {m_{1}}{3}}\right)} .}
Інтерполяція сплайном Інтерполяції набору точок
(
x
k
,
p
k
)
{\displaystyle (x_{k},{\boldsymbol {p}}_{k})}
k
=
1
,
…
,
n
{\displaystyle \ k=1,\ldots ,n}
(
x
1
,
x
n
)
.
{\displaystyle \ (x_{1},x_{n}).}
Існують декілька способів задання параметрів.
Кінцеві різниці Найпростіший спосіб із застосуванням трьох контрольних точок:
m
k
=
p
k
+
1
−
p
k
2
(
x
k
+
1
−
x
k
)
+
p
k
−
p
k
−
1
2
(
x
k
−
x
k
−
1
)
{\displaystyle {\boldsymbol {m}}_{k}={\frac {{\boldsymbol {p}}_{k+1}-{\boldsymbol {p}}_{k}}{2(x_{k+1}-x_{k})}}+{\frac {{\boldsymbol {p}}_{k}-{\boldsymbol {p}}_{k-1}}{2(x_{k}-x_{k-1})}}}
для індексів
k
=
2
,
…
,
n
−
1
{\displaystyle k=2,\ldots ,n-1}
Кардинальні сплайни
m
k
=
(
1
−
c
)
p
k
+
1
−
p
k
−
1
2
{\displaystyle {\boldsymbol {m}}_{k}=(1-c){\frac {{\boldsymbol {p}}_{k+1}-{\boldsymbol {p}}_{k-1}}{2}}}
Параметр
c
∈
(
0
,
1
)
{\displaystyle c\in (0,1)}
Сплайни Кетмал-Рома
m
k
=
p
k
+
1
−
p
k
−
1
2
{\displaystyle {\boldsymbol {m}}_{k}={\frac {{\boldsymbol {p}}_{k+1}-{\boldsymbol {p}}_{k-1}}{2}}}
![{\displaystyle \mathbf {p} (t)=h_{00}(t)\mathbf {p_{0}} +h_{10}(t)\mathbf {m_{0}} +h_{01}(t)\mathbf {p_{1}} +h_{11}(t)\mathbf {m_{1}} ,\qquad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ea37ce43183b72d3917aa76eadf1324d4e10139)
