Евольвента

Приклад побудови евольвенти кривої

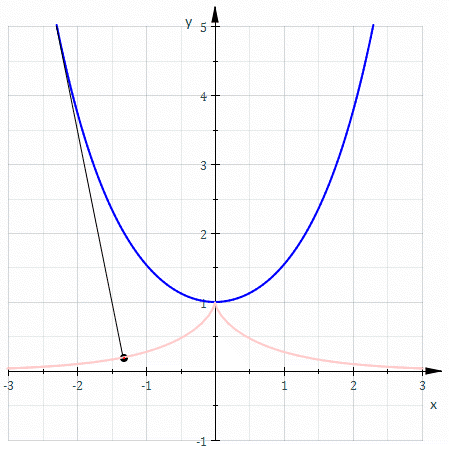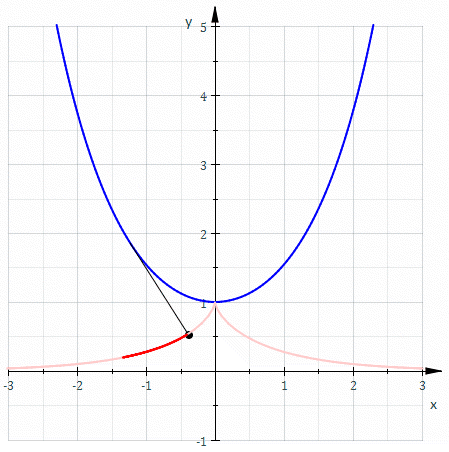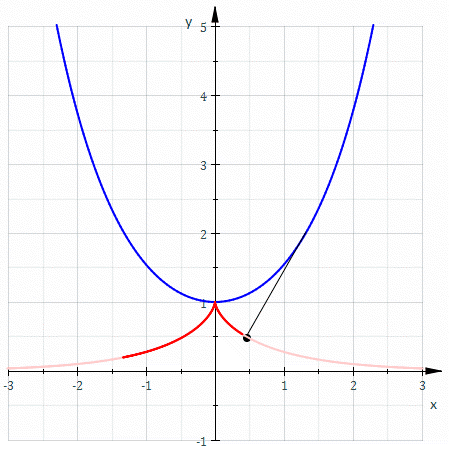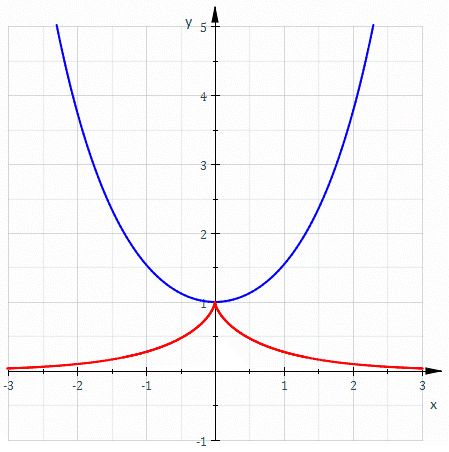
Евольвента (від лат. evolvens — що розгортає) плоскої лінії $L$  — це лінія $L_{*}$, по відношенню до якої $L$ є еволютою. Іншими словами, це крива, що описується кінцем гнучкої нерозтяжної нитки закріпленої в деякій точці, що змотується з плоскої кривої.

Рівняння евольвенти

Якщо лінія $l$ задана рівнянням ${\bar {r}}={\bar {r}}(s)\$ ($s$ — параметр довжини кривої), то рівняння властивості її евольвенти має вигляд

${\bar {\psi }}={\bar {r}}+(\alpha -s){\dot {\bar {r}}}$,

де $\alpha$ — довільний параметр.

Для параметрично заданої кривої $(x(t),y(t))$ рівняння евольвенти

$X(t)=x(t)-{\frac {x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,dt$

$Y(t)=y(t)-{\frac {y(t)'}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\,dt$

Приклад

Анімація побудови евольвенти кола

Евольвентою кола є спіралеподібна крива, котра описується кінцем гнучкої нерозтяжної нитки, що змотується з кола заданого радіуса. Рівняння евольвенти кола мають вигляд:

$~x=r(\cos(t)+t\sin(t))$

$~y=r(\sin(t)-t\cos(t))$

де $t$ — кут положення на колі точки дотику нитки до кола, a $r$ — радіус кола.

Побудова евольвенти кола заданого діаметра

Евольвента кола

Задане коло з діаметром $d\!$, з центром в точці $o\!$. Дане коло ділимо на дванадцять рівних частин. В точках 2, 3, 4. проводимо дотичні до кола, спрямовані в один бік. Точки евольвенти знаходимо виходячи з того, що при розгортанні кола точка $B^{2}\!$, повинна розміщатись від точки 2 на відстані, рівній довжині дуги між точками 1 і 2, а точка $B^{3}\!$, повинна розміщатись від точки 3 на відстані, рівній довжині дуги між точками 1 і 3 (дві довжини попередньої дуги), і так далі

Точне розташування точок евольвенти отримаємо, відкладаючи по дотичних довжини відповідних дуг. Довжину дуги між точками 1 і 2 визначається за формулою

$a={\frac {\pi d}{m}},\!$

де $d\!$ — діаметр кола; $m\!$ — число частин, на яке розділено коло.

Отримавши низку точок евольвенти сполучаємо їх плавною лінією.

В даному випадку коло з діаметром $d\!$ є еволютою до цієї евольвенти.

Застосування

У техніці форму евольвенти кола мають:

• профіль зуба для коліс зубчастої передачі;
• форма кожуха радіального вентилятора;
• вихори потоків у циклонах та ін.

У системах автоматизованого проектування іноді використовують кубічні криві Безьє для наближеного опису евольвентних кривих у евольвентних зачепленнях.

Див. також

• Еволюта
• Евольвентне зачеплення
• Паралельна крива

Посилання

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1400+ с.(укр.)
• Mathworld. Involute [Архівовано 11 лютого 2021 у Wayback Machine.]