Векторний добуток

Векторний добуток (вертикальний вектор) змінюється разом з кутом між векторами

Ве́кторний добу́ток — білінійна, антисиметрична операція на векторах у тривимірному просторі. На відміну від скалярного добутку векторів евклідового простору, результатом векторного добутку є вектор (його також називають «векторним добутком»), а не скаляр.

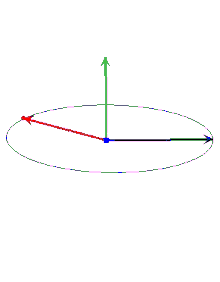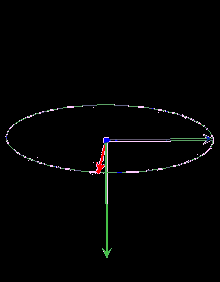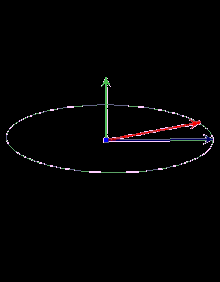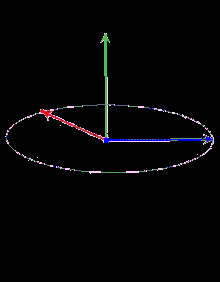
Векторний добуток двох векторів у тривимірному евклідовому просторі — вектор, перпендикулярний до обох вихідних векторів, довжина якого дорівнює площі паралелограма, утвореного вихідними векторами, а вибір з двох напрямків визначається так, щоб трійка з векторів-множників, узятих в такому ж порядку, як записано в добутку, і отриманого вектора була правою. Векторний добуток колінеарних векторів (зокрема, якщо хоча б один з множників — нульовий вектор) вважається рівним нульовому вектору.

Таким чином, для визначення векторного добутку двох векторів необхідно задати орієнтацію простору, тобто сказати, яка трійка векторів є правою, а яка — лівою. При цьому не є обов'язковим задання у розглянутому просторі будь-якої системи координат. Зокрема, при заданій орієнтації простору результат векторного добутку не залежить від того, чи є розглядувана система координат правою, чи лівою. При цьому формули вираження координат векторного добутку через координати вихідних векторів у правій і лівій ортонормованій прямокутній системі координат відрізняються знаком.

Векторний добуток не має властивості комутативності та асоціативності. Він є антикомутативним і, на відміну від скалярного добутку векторів, результат є знову вектором.

Корисний для «вимірювання» перпендикулярності векторів — модуль векторного добутку двох векторів дорівнює добутку їхніх модулів, якщо вони перпендикулярні, і зменшується до нуля, якщо вектори колінеарні.

Має багато технічних і фізичних застосувань. Наприклад, момент імпульсу і сила Лоренца математично записуються у вигляді векторного добутку.

Історія

Векторний добуток було введено У. Гамільтоном у 1846 році одночасно зі скалярним добутком у зв'язку з кватерніонами — відповідно, як векторна і скалярна частина добутку двох кватерніонів, скалярна частина яких дорівнює нулю.

Позначення

Найчастіше для позначення векторного добутку вживається символ ×. Векторний добуток позначається також квадратними дужками, в яких співмножники розділені комами. Крім того, в фізичних текстах заведено позначати вектори жирним шрифтом.

${\vec {u}}\times {\vec {v}}=[{\vec {u}},{\vec {v}}]=[{\vec {u}}\times {\vec {v}}]=\mathbf {u} \times \mathbf {v} =[\mathbf {u} ,\mathbf {v} ]$

Праві і ліві трійки векторів у тривимірному евклідовому просторі

Розглянемо впорядковану трійку некомпланарних (лінійно незалежних) векторів ${\vec {a}},{\vec {b}},{\vec {c}}$ в тривимірному евклідовому просторі. В орієнтованому просторі така трійка векторів буде або «правою», або «лівою».

Геометричне визначення

Сумісний початки векторів в одній точці. Упорядкована трійка некомпланарних векторів ${\vec {a}},{\vec {b}},{\vec {c}}$ у тривимірному просторі називається правою, якщо з кінця вектора ${\vec {c}}$ найкоротший поворот від вектора ${\vec {a}}$ до вектору ${\vec {b}}$ видно спостерігачеві проти годинникової стрілки. І навпаки, якщо найкоротший поворот видно за годинниковою стрілкою, то трійка називається лівою.

Визначення за допомогою руки

Знаходження напрямку векторного добутку використовуючи правило правої руки

Інше визначення пов'язане з правою рукою людини, звідки і взято назву. На малюнку трійка векторів ${\vec {a}}$, ${\vec {b}}$, ${\vec {a}}\times {\vec {b}}$ є правою.

Алгебричне визначення

Існує також аналітичний спосіб визначення правої і лівої трійки векторів, який вимагає задання у розглянутому просторі правої або лівої системи координат, причому не обов'язково прямокутної і ортонормованої.

Потрібно скласти матрицю, першим рядком якої будуть координати вектора ${\vec {a}}$, другим — вектора ${\vec {b}}$, третім — вектора ${\vec {c}}$. Потім, залежно від знака визначника цієї матриці, можна зробити такі висновки:

• Якщо визначник додатний, то трійка векторів має ту ж орієнтацію, що й система координат.
• Якщо визначник від'ємний, то трійка векторів має орієнтацію, протилежну орієнтації системи координат.
• Якщо визначник дорівнює нулю, то вектори компланарні (лінійно залежні).

Зауваження

Визначення «правої» і «лівої» трійки векторів залежать від орієнтації простору, але не вимагають задання у розглянутому просторі будь-якої системи координат, як і не вимагає цього визначення самого векторного добутку. При цьому формули вираження координат векторного добутку через координати вихідних векторів будуть відрізнятися знаком у правій і лівій прямокутній системі координат.

Всі праві між собою (і ліві між собою) трійки векторів називаються однаково орієнтованими.

За заданої орієнтації простору система координат називається правою (лівою), якщо трійка з векторів з координатами $(1,0,0)$, $(0,1,0)$, $(0,0,1)$ є правою (лівою).

Геометричне визначення і визначення за допомогою руки самі задають орієнтацію простору. Алгебраїчне визначення задає спосіб розбиття трійок некомпланарних векторів на два класи однаково орієнтованих векторів, але воно не задає орієнтації простору, а використовує вже задану — ту, на підставі якої дана система координат вважається правою або лівою. При цьому, якщо орієнтація системи координат невідома, можна порівнювати знак визначника зі знаком визначника іншої трійки некомпланарних векторів, орієнтація якої відома — якщо знаки збігаються, то трійки однаково орієнтовані, якщо знаки протилежні — трійки протилежно орієнтовані.

Алгебраїчне означення векторного добутку

Довільний вектор в $\mathbb {R} ^{3}$ описується своїми координатами відносно стандартного базису $\{{\vec {i}},{\vec {j}},{\vec {k}}\}.$ Векторним добутком двох $3$-векторів

${\vec {u}}=u_{1}{\vec {i}}+u_{2}{\vec {j}}+u_{3}{\vec {k}},\quad {\vec {v}}=v_{1}{\vec {i}}+v_{2}{\vec {j}}+v_{3}{\vec {k}},$

називається $3$-вектор

${\vec {u}}\times {\vec {v}}=(u_{2}v_{3}-u_{3}v_{2}){\vec {i}}+(u_{3}v_{1}-u_{1}v_{3}){\vec {j}}+(u_{1}v_{2}-u_{2}v_{1}){\vec {k}},$

який також символічно записується у вигляді $3\times 3$ детермінанту:

${\vec {u}}\times {\vec {v}}={\begin{vmatrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\end{vmatrix}}$.

Насправді ці формули для векторного добутку виконуються у будь-якому ортонормованому базисі $\mathbb {R} ^{3}$.

Геометричне означення векторного добутку

У науковій літературі з механіки і фізики розповсюджено дещо інше означення векторного добутку.

Векторним добутком двох $3$-векторів ${\vec {u}},{\vec {v}}\in \mathbb {R} ^{3}$ називається $3$-вектор ${\vec {u}}\times {\vec {v}}\in \mathbb {R} ^{3}$, який задовольняє наступним вимогам:

1. $|{\vec {u}}\times {\vec {v}}|=|{\vec {u}}||{\vec {v}}|\sin \theta ,$ де $\theta$ —це кут між ${\vec {u}}$ та ${\vec {v}}$ (довжина або правило паралелограму);
2. вектор ${\vec {u}}\times {\vec {v}}$ — ортогональний до векторів ${\vec {u}}$ та ${\vec {v}}$ (ортогональність);
3. вектори ${\vec {u}},{\vec {v}},{\vec {u}}\times {\vec {v}}$ утворюють праву трійку векторів (орієнтація).

Властивості

Геометричні властивості векторного добутку

Малюнок 1: Площа паралелограма дорівнює модулю векторного добутку.

Малюнок 2: Об'єм паралелепіпеда при використанні векторного і скалярного добутку векторів; пунктирні лінії показують проєкції вектора c на a × b і вектора b × c на a. Це відповідає різним способам обчислення об'єму.

• Необхідною і достатньою умовою колінеарності двох ненульових векторів є рівність нулю їх векторного добутку.
• Модуль векторного добутку $[{\vec {a}},\;{\vec {b}}]$ дорівнює площі $S$ паралелограма, побудованого на зведених до спільного початку векторах ${\vec {a}}$ і ${\vec {b}}$ (див. малюнок 1)
• Якщо ${\vec {e}}$ — одиничний вектор, ортогональний векторам ${\vec {a}}$ і ${\vec {b}}$ і вибраний так, що трійка ${\vec {a}},{\vec {b}},{\vec {e}}$ — права, а $S$ — площа паралелограма, побудованого на них (зведених до спільного початку), то для векторного добутку справедлива формула:

$[{\vec {a}},\;{\vec {b}}]=S\cdot {\vec {e}}.$

• Якщо ${\vec {c}}$ — який-небудь вектор, $\pi$ — будь-яка площина, яка містить цей вектор, ${\vec {e}}$ — одиничний вектор, що лежить у площині $\pi$ і ортогональний до ${\vec {c}}$, ${\vec {g}}$ — одиничний вектор, ортогональний до площини $\pi$ і спрямований так, що трійка векторів ${\vec {e}},{\vec {c}},{\vec {g}}$ є правою, то для будь-якого вектора ${\vec {a}}$, що лежить у площині $\pi$, справедлива формула

$[{\vec {a}},\;{\vec {c}}]=\mathrm {Pr} _{\vec {e}}{\vec {a}}\cdot |{\vec {c}}|\cdot {\vec {g}}.$

• При використанні векторного і скалярного добутків можна вирахувати об'єм паралелепіпеда, побудованого на зведених до спільного початку векторах a, b і c (див. малюнок 2). Такий добуток трьох векторів називається мішаним.

$V=|\langle {\vec {a}},\;[{\vec {b}},\;{\vec {c}}]\rangle |.$

На малюнку показано, що цей об'єм може бути знайдений двома способами: геометричний результат зберігається навіть при заміні «скалярного» і «векторного» добутків місцями:

$V=\langle [{\vec {a}},\;{\vec {b}}],\;{\vec {c}}\rangle =\langle {\vec {a}},\;[{\vec {b}},\;{\vec {c}}]\rangle .$

Величина векторного добутку залежить від синуса кута між початковими векторами, тому векторний добуток може сприйматися як степінь «перпендикулярності» векторів так само, як і скалярний добуток може розглядатися як степінь «паралельності». Векторний добуток двох одиничних векторів дорівнює 1 (одиничного вектора), якщо початкові вектори перпендикулярні, і дорівнює 0 (нульовому вектору), якщо вектори паралельні або антипаралельні.

Алгебричні властивості векторного добутку

Далі $[{\vec {a}},\;{\vec {b}}]$ і $\langle {\vec {a}},\;{\vec {b}}\rangle$ позначають відповідно векторний і скалярний добуток векторів ${\vec {a}}$ і ${\vec {b}}$.

Подання	Опис
$[{\vec {a}},\;{\vec {b}}]=-[{\vec {b}},{\vec {a}}]$	Антикомутативність.
$[\alpha \cdot {\vec {a}},\;{\vec {b}}]=[{\vec {a}},\;\alpha \cdot {\vec {b}}]=\alpha \cdot [{\vec {a}},\;{\vec {b}}]$	Ассоціативність множення на скаляр.
$[{\vec {a}}+{\vec {b}},\;{\vec {c}}]=[{\vec {a}},\;{\vec {c}}]+[{\vec {b}},\;{\vec {c}}]$	Дистрибутивність за додаванням.
$[[{\vec {a}},\;{\vec {b}}],\;{\vec {c}}]+[[{\vec {b}},\;{\vec {c}}],\;{\vec {a}}]+[[{\vec {c}},{\vec {a}}],\;{\vec {b}}]=0$	Тотожність Якобі.
$[{\vec {a}},\;{\vec {a}}]={\vec {0}}$
$[{\vec {a}},\;[{\vec {b}},\;{\vec {c}}]]={\vec {b}}\cdot \langle {\vec {a}},\;{\vec {c}}\rangle -{\vec {c}}\cdot \langle {\vec {a}},\;{\vec {b}}\rangle$	Формула «БАЦ мінус ЦАБ», тотожність Лагранжа.
$|[{\vec {a}},\,{\vec {b}}]|^{2}+\langle {\vec {a}},\,{\vec {b}}\rangle ^{2}=|{\vec {a}}|^{2}\cdot |{\vec {b}}|^{2}$	Частковий випадок мультиплікативності норми кватерніонів.
$\langle [{\vec {a}},\,{\vec {b}}],\,{\vec {c}}\rangle =\langle {\vec {a}},\,[{\vec {b}},\,{\vec {c}}]\rangle$	Значення цього виразу називають мішаним добутком векторів $a$, $b$, $c$.

Вираження в координатах

У правому ортонормованому базисі

Якщо два вектори ${\vec {a}}$ і ${\vec {b}}$ подані у правому ортонормованому базисі координатами

${\vec {a}}=(a_{x},\;a_{y},\;a_{z}),$

${\vec {b}}=(b_{x},\;b_{y},\;b_{z}),$

то їх векторний добуток має координати

$[{\vec {a}},\;{\vec {b}}]=(a_{y}b_{z}-a_{z}b_{y},\;a_{z}b_{x}-a_{x}b_{z},\;a_{x}b_{y}-a_{y}b_{x}).$

Для запам'ятовування цієї формули зручно використовувати символічний визначник:

$[{\vec {a}},\;{\vec {b}}]={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\end{vmatrix}},$

де $\mathbf {i} =(1,0,0)$, $\mathbf {j} =(0,1,0)$, $\mathbf {k} =(0,0,1)$, або

$[{\vec {a}},\;{\vec {b}}]_{i}=\sum _{j,k=1}^{3}\varepsilon _{ijk}a_{j}b_{k},$

де $\varepsilon _{ijk}$ — символ Леві-Чивіти.

У лівому ортонормованому базисі

Якщо базис лівий ортонормований, то векторний добуток у координатах має вигляд

$[{\vec {a}},\;{\vec {b}}]=(a_{z}b_{y}-a_{y}b_{z},\;a_{x}b_{z}-a_{z}b_{x},\;a_{y}b_{x}-a_{x}b_{y}).$

Для запам'ятовування, аналогічно:

$[{\vec {a}},\;{\vec {b}}]=-{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\end{vmatrix}},$

або

$[{\vec {a}},\;{\vec {b}}]_{i}=-\sum _{j,k=1}^{3}\varepsilon _{ijk}\cdot a_{j}\cdot b_{k}.$

Формули для лівої системи координат можна отримати з формул правої системи координат, записавши ті ж вектори ${\vec {a}}$ і ${\vec {b}}$ у допоміжній правій системі координат ($\mathbf {i} '=\mathbf {i} ,\mathbf {j} '=\mathbf {j} ,\mathbf {k} '=-\mathbf {k}$):

$[{\vec {a}},\;{\vec {b}}]={\begin{vmatrix}\mathbf {i} '&\mathbf {j} '&\mathbf {k} '\\a'_{x}&a'_{y}&a'_{z}\\b'_{x}&b'_{y}&b'_{z}\end{vmatrix}}={\begin{vmatrix}\mathbf {i} &\mathbf {j} &-\mathbf {k} \\a_{x}&a_{y}&-a_{z}\\b_{x}&b_{y}&-b_{z}\end{vmatrix}}=-{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\end{vmatrix}}.$

У довільній афінній системі координат

Векторний добуток у довільній афінній системі координат $O{\vec {e}}_{1}{\vec {e}}_{2}{\vec {e}}_{3}$ має координати

$[{\vec {a}},\;{\vec {b}}]={\begin{vmatrix}[{\vec {e}}_{2},\;{\vec {e}}_{3}]&[{\vec {e}}_{3},\;{\vec {e}}_{1}]&[{\vec {e}}_{1},\;{\vec {e}}_{2}]\\a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\end{vmatrix}}.$

Варіації та узагальнення

Кватерніони

Координати векторного добутку в правому ортонормованому базисі можна також записати в кватерніонній формі, тому букви $\mathbf {i}$, $\mathbf {j}$, $\mathbf {k}$ — стандартні позначення для ортів в $\mathbb {R} ^{3}$: вони розглядаються як уявні кватерніони.

Зауважимо, що співвідношення через векторний добуток між $\mathbf {i}$, $\mathbf {j}$ і $\mathbf {k}$ відповідають правилам множення для кватерніонів $i$, $j$ і $k$. Якщо уявити вектор $(a_{1},\;a_{2},\;a_{3})$ як кватерніон $a_{1}i+a_{2}j+a_{3}k$, то векторний добуток двох векторів виходить взяттям векторної частини від добутку відповідних їм кватерніонів. Скалярний добуток цих векторів протилежний скалярній частині добутку цих кватерніонів.

Перетворення до матричної форми

Векторний добуток двох векторів у координатах у правому ортонормованому базисі можна записати як добуток кососиметричної матриці і вектора:

$[{\vec {a}},\;{\vec {b}}]=[{\vec {a}}]_{\times }{\vec {b}}={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}},$

$[{\vec {b}},\;{\vec {a}}]={\vec {b}}^{T}[{\vec {a}}]_{\times }={\begin{bmatrix}b_{1}&b_{2}&b_{3}\end{bmatrix}}{\begin{bmatrix}\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&\,0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}},$

де

$[{\vec {a}}]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.$

Нехай ${\vec {a}}$ дорівнює векторному добутку:

${\vec {a}}=[{\vec {c}},\;{\vec {d}}],$

тоді

$[{\vec {a}}]_{\times }=({\vec {c}}{\vec {d}}^{T})^{T}-{\vec {c}}{\vec {d}}^{T}.$

Така форма запису дозволяє узагальнити векторний добуток на вищі розмірності, подаючи псевдовектори (кутова швидкість, індукція тощо) як такі кососиметричні матриці. Ясно, що такі фізичні величини будуть мати $n(n-1)/2$ незалежних компонент у $n$-вимірному просторі. У тривимірному просторі виходять три незалежні компоненти, тому такі величини можна подавати як вектори цього простору.

З такою формою запису також здебільшого простіше працювати (наприклад, в епіполярній геометрії).

Із загальних властивостей векторного добутку випливає, що

$[{\vec {a}}]_{\times }\,{\vec {a}}={\vec {0}}$ і ${\vec {a}}^{T}\,[{\vec {a}}]_{\times }={\vec {0}},$

а оскільки $[{\vec {a}}]_{\times }$ кососиметрична, то

${\vec {b}}^{T}\,[{\vec {a}}]_{\times }\,{\vec {b}}=0.$

У такій формі запису легко довести тотожність Лагранжа (правило «БАЦ мінус ЦАБ»).

Поширення на матриці

У тривимірному випадку можна визначити в координатах у довільному базисі векторний добуток матриць і добуток матриці на вектор. Це робить очевидним зазначений вище ізоморфізм і дозволяє спростити багато викладок. Подамо матрицю $A$ як стовпець векторів, тоді

${\begin{bmatrix}{\vec {a}}_{1}\\{\vec {a}}_{2}\\{\vec {a}}_{3}\end{bmatrix}}\times {\vec {b}}={\begin{bmatrix}{\vec {a}}_{1}\times {\vec {b}}\\{\vec {a}}_{2}\times {\vec {b}}\\{\vec {a}}_{3}\times {\vec {b}}\end{bmatrix}},$

${\begin{bmatrix}{\vec {a}}_{1}\\{\vec {a}}_{2}\\{\vec {a}}_{3}\end{bmatrix}}\cdot {\vec {b}}={\begin{bmatrix}{\vec {a}}_{1}\cdot {\vec {b}}\\{\vec {a}}_{2}\cdot {\vec {b}}\\{\vec {a}}_{3}\cdot {\vec {b}}\end{bmatrix}}.$

Множення матриці на вектор зліва визначається аналогічно, якщо подати $A$ як рядок векторів. Транспонування матриці, відповідно, переводить рядок векторів у стовпець векторів, і навпаки. Легко узагальнити багато співвідношень для векторів на співвідношення для векторів і матриць, наприклад ($A$ — матриця, ${\vec {x}}$, ${\vec {y}}$ — вектори):

$A\cdot ({\vec {x}}\times {\vec {y}})=(A\times {\vec {x}})\cdot {\vec {y}},$

$A\times ({\vec {x}}\times {\vec {y}})={\vec {x}}(A\cdot {\vec {y}})-{\vec {y}}(A\cdot {\vec {x}}).$

Після цього можна змінити форму запису для векторного добутку:

${\vec {x}}\times {\vec {y}}=E\cdot ({\vec {x}}\times {\vec {y}})=(E\times {\vec {x}})\cdot {\vec {y}},$

$E$ — одинична матриця. Звідси очевидні існування і вигляд матриці, що відповідає векторному множенню на вектор ліворуч. Аналогічно можна отримати вираз для множення матриці на вектор праворуч. Поширюючи операції над векторами на матриці покомпонентно, подаючи їх як «вектори з векторів», стандартні співвідношення для векторів легко узагальнюються на матриці. Наприклад, теорема Стокса в $\mathbb {R} ^{3}$ набуде вигляду:

$\int \limits _{\Sigma }\operatorname {rot} \,\mathbf {A^{T}} \,\mathbf {d\Sigma } =\int \limits _{\partial \Sigma }\mathbf {A} \cdot \,d\mathbf {r} ,$

де ротор матриці $A$ обчислюється як векторний добуток матриці $A$ на оператор Гамільтона зліва (базис вважається правим ортонормованим). У цих позначеннях дуже легко довести, наприклад, такі форми теореми Стокса:

$\int \limits _{\Sigma }\operatorname {grad} \,u\times \,\mathbf {d\Sigma } =\int \limits _{\partial \Sigma }u\,d\mathbf {r} ,$

$\int \limits _{\Sigma }\left[\mathbf {d\Sigma } ;\left[\nabla ;\mathbf {a} \right]\right]=\int \limits _{\partial \Sigma }\mathbf {a} \times d\mathbf {r} .$

Розмірності, не рівні трьом

Нехай $n$ — розмірність простору.

Векторний добуток, що володіє всіма властивостями звичайного тривимірного векторного добутку, тобто бінарне білінійне антисиметричне невироджене відображення $\mathbb {R} ^{n}\times \mathbb {R} ^{n}\to \mathbb {R} ^{n}$можна ввести тільки для розмірностей 3 і 7.

Однак є просте узагальнення на інші натуральні виміри, починаючи з 3, а якщо потрібно — і на розмірність 2 (останнє, щоправда, дещо специфічним чином). Тоді це узагальнення, на відміну від неможливого, описаного трохи вище, вводиться не для пари векторів, а лише для набору $(n-1)$ векторів-співмножників. Цілком аналогічно мішаному добутку, природно узагальнюваному в $n$-вимірному просторі на операцію з $n$ співмножниками. Використовуючи символ Леві-Чивіти $\varepsilon _{i_{1}i_{2}i_{3}\ldots i_{n}}$ з $n$ індексами можна явно записати такий $(n-1)$-валентний векторний добуток як

$P_{i}(\mathbf {a,\;b,\;c,\;\ldots } )=\sum _{j,\;k,\;m,\;\ldots =1}^{n}\varepsilon _{ijk\ldots }a_{j}b_{k}c_{m}\ldots =\det({\begin{pmatrix}\mathbf {e_{1}} \\\vdots \\\mathbf {e_{n}} \end{pmatrix}}\mathbf {,a,b,c,\ldots } )\cdot \mathbf {e_{i}} ,$

Таке узагальнення дає гіперплощу розмірності $n-1$.

Якщо потрібно ввести операцію саме для двох співмножників, що має геометричний сенс, гранично близький до змісту векторного добутку (тобто представляє орієнтовану площу), то результат вже не буде вектором, оскільки при $n\neq 3$ не знайдеться єдиної, однозначно визначеної нормалі до двовимірної площини, натягнутої на множники. Можна ввести бівектор, компоненти якого дорівнюють проєкціям орієнтованої площі паралелограма, натягнутого на пару векторів, на координатні площини:

$\ P_{ij}(\mathbf {a,b} )=a_{i}b_{j}-a_{j}b_{i}$.

Ця конструкція називається зовнішнім добутком.

Для двовимірного випадку операція

$\ P(\mathbf {a,b} )=a_{1}b_{2}-a_{2}b_{1}$.

називається псевдоскалярним добутком, оскільки отримуваний простір одновимірний і результат є псевдоскаляром. (Двоіндексний зовнішній добуток, описаний вище, можна ввести і для двовимірного простору, однак він, очевидно, досить тривіально пов'язаний зі псевдоскалярним добутком, а саме зовнішній добуток у цьому випадку подається матрицею, на діагоналі якої нулі, а два недіагональні елементи, що залишилися, дорівнюють псевдоскалярному добутку і мінус псевдоскалярному добутку).

Алгебра Лі векторів

Векторний добуток вводить на $\mathbb {R} ^{3}$ структуру алгебри Лі (оскільки він задовольняє обом аксіомам — антисиметричності і тотожності Якобі). Ця структура відповідає ототожненню $\mathbb {R} ^{3}$ з дотичною алгеброю Лі $so(3)$ до групи Лі $SO(3)$ ортогональних лінійних перетворень тривимірного простору.

Див. також

• Скалярний добуток
• Аксіальний вектор
• Псевдоскалярний добуток (тільки на площині!)
• Мішаний (скалярно-векторний) добуток векторів (тільки в $\mathbb {R} ^{3}$)
• Подвійний (векторно-векторний) добуток векторів (тільки в $\mathbb {R} ^{3}$)
• Векторний добуток у семивимірному просторі

Інше

• Ротор
• Дивергенція

Посилання

• Добуток векторний // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.