Правильногранний многогранник



Правильногранний многогранник — це опуклий многогранник, кожна грань якого є правильним многокутником.
Правильногранний многогранник називають тілом Джонсона або многогранником Джонсона, якщо він не є ні платоновим тілом (правильним многогранником), ні архімедовим, ні призмою, ні антипризмою.
Прикладом тіла Джонсона є піраміда з квадратною основою і бічними гранями у вигляді правильних трикутників (J1(М2)). Вона має 1 квадратну грань і 4 трикутних.
Як і в кожного строго опуклого тіла, в цих многогранників до кожної вершини примикає щонайменше три грані і сума їхніх кутів (прилеглих до вершини) менша від 360º. Оскільки правильні многокутники мають кути щонайменше 60º, до вершини можуть прилягати максимум п'ять граней. П'ятикутна піраміда[en] (J2) є прикладом, у якому є вершина п'ятого порядку (тобто з п'ятьма гранями).
Хоча немає явного обмеження на правильні многокутники, які можуть служити гранями тіл Джонсона, насправді грані можуть мати тільки 3, 4, 5, 6, 8 або 10 сторін, причому трикутні грані (не менше чотирьох) має будь-яке з тіл Джонсона.
Подовжений чотирисхилий повернутий бікупол (J37), який називають також псевдоромбокубооктаедром[1] єдиний з тіл Джонсона має властивість локальної вершинної однорідності — в кожній вершині сходяться 4 грані і їхнє розташування однакове — 3 квадрати і 1 трикутник. Однак тіло вершинно-транзитивним не є, оскільки має різну ізометрію в різних вершинах, що й робить його тілом Джонсона, а не архімедовим тілом.
1966 року Норман Джонсон[en] опублікував список усіх 92 тіл і дав їм назви й номери. Він висловив гіпотезу, що їх тільки 92, тобто інших немає.
Раніше, 1946 року Л. Н. Єсаулова надіслала О. Д. Александрову листа, в якому довела, що правильногранних многогранників (крім 5 правильних многогранників, 13 напівправильних і двох нескінченних серій (призм та антипризм) може існувати лише скінченне число. 1961 року Александров передав цього листа В. А. Залгаллеру[ru], можливо через нотатки Джонсона 1960 року.[2] 1967 року Залгаллер опублікував доведення того, що список Джонсона повний. До виконання було залучено групу школярів школи № 239. Повне доведення зайняло близько 4 років з залученням комп'ютерної техніки. В доведенні також істотно використовувалась теорема Александрова про опуклі многогранники.
Назви тіл Джонсона мають велику описову здатність. Більшість цих тіл можна побудувати з кількох тіл (пірамід, куполів і ротонд), додаючи платонові і архімедові тіла, призми й антипризми.
- Бі- означає, що дві копії тіл з'єднані основами. Для куполів і ротонд вони можуть бути з'єднані гранями одного типу (прямі) або різних (повернуті). Октаедр, наприклад, є квадратною біпірамідою, кубооктаедр — повернутим трикутним бікуполом, а ікосододекаедр — повернутою п'ятикутною біротондою.
- Подовжений означає, що до тіла приєднано призму або її вставлено між двома частинами тіла. Ромбокубооктаедр, наприклад, є подовженим квадратним прямим куполом.
- Скручений подовжений означає, що до тіла приєднано антипризму або її вставлено між двома частинами тіла. Ікосаедр, наприклад, є скрученою подовженою п'ятикутною біпірамідою.
- Нарощений означає, що піраміда або купол приєднані до грані тіла.
- Відсічений означає, що піраміду або купол відрізано від тіла.
- Скручений означає, що купол, який належить многограннику, повернуто так само, як у повернутих бікуполах.
Останні три операції — нарощення, відсікання і поворот — на досить великих многогранниках можуть бути виконані більше одного разу. Для операцій, здійснених два рази, додається двічі. (Двічі скручене тіло має два повернутих куполи.) Для операцій, виконаних три рази, додається тричі. (У тричі відсіченого тіла видалено три піраміди або куполи.)
Іноді слова двічі недостатньо. Необхідно відрізняти тіла, в яких змінено дві протилежні грані від тіл, в яких змінено інші грані. Коли змінені грані паралельні, до назви додається протилежно. (Двічі протилежно нарощене тіло має дві паралельні грані (протилежні) з доданими тілами.) Якщо ж зміни стосуються граней, які не є протилежними, до назви додається, косо. (Двічі косо нарощене тіло має дві грані з доданими тілами, але ці грані не протилежні.)
Кілька назв походять від многокутників, з яких зібрано тіло Джонсона.
- Якщо визначити місяць як групу з двох трикутників, приєднаних до квадрата, слово клинокорона відповідає клиноподібній короноподібній групі, утвореній двома місяцями. Слово двоклиноїд або двоклинник означає дві такі групи.
У цій статті використовуються назви зі статті Залгаллера[3]. Разом з номерами многогранників, даними Джонсоном, у дужках наведено складений номер зі статті Залгаллера. У цьому складеному номері
- Пn позначає призму з n-кутною основою.
- Аn позначає антипризму з n-кутною основою.
- Мn позначає тіло з індексом n (тобто в цьому випадку тіло будується на основі іншого тіла).
- Підкреслення означає поворот тіла.
Зауваження: Мn не збігається з Jn. Так, квадратна піраміда J1(М2) має індекс 1 у Джонсона і індекс 2 у Залгаллера.
Перші два тіла Джонсона, J1 і J2, є пірамідами. Трикутна піраміда є правильним тетраедром, тобто не є тілом Джонсона.
| Правильні | J1(М2) | J2(М3) |
|---|---|---|
| Трикутна піраміда (тетраедр) |
Квадратна піраміда | П'ятикутна піраміда[en] |

|

|

|

|

|

|
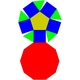
Наступні чотири многогранники — три куполи й одна ротонда.
| Куполи | Ротонди | |||
|---|---|---|---|---|
| Однорідні | J3(М4) | J4(М5) | J5(М6) | J6(М9) |
| Трикутна призма | Трисхилий купол | Чотирисхилий купол | П'ятисхилий купол | П'ятисхила ротонда |

|

|

|

|

|

|

|
|

| |
| Пов'язані однорідні многогранники | ||||
| Кубооктаедр | Ромбокубооктаедр | Ромбоікосододекаедр | Ікосододекаедр | |

|

|

|

| |
Наступні п'ять многогранників Джонсона є подовженими і скрученими подовженими пірамідами. Їх отримують склеюванням двох многогранників. У разі скрученої подовженої трикутної піраміди три пари суміжних трикутників копланарні, тобто тіло не є многогранником Джонсона.
| Подовжені піраміди[en] (або нарощені призми) |
Скручені подовжені піраміди[en] (або нарощені антипризми) | ||||
|---|---|---|---|---|---|
| J7(М1+П3) | J8(М2+П4) | J9(М3+П5) | Копланарна | J10(М2+А4) | J11(М3+А5) |
| Подовжена трикутна піраміда | Подовжена чотирикутна піраміда | Подовжена п'ятикутна піраміда | Скручена подовжена трикутна піраміда | Скручена подовжена чотирикутна піраміда | Скручена подовжена п'ятикутна піраміда |
| Нарощена трикутна призма | Нарощений куб | Нарощена п'ятикутна призма | Нарощений октаедр | Нарощена квадратна антипризма | Нарощена п'ятикутна антипризма |

|

|

|

|

|

|

|

|

|

|

| |
| Утворені з многогранників | |||||
| Тетраедр Трикутна призма |
Квадратна піраміда Куб |
П'ятикутна піраміда[en] П'ятикутна призма |
Тетраедр Октаедр |
Квадратна піраміда Квадратна антипризма |
П'ятикутна піраміда[en] П'ятикутна антипризма |
Наступними многогранниками Джонсона є біпіраміди, подовжені біпіраміди[en] і скручені подовжені біпіраміди[en]:
| Біпіраміди | Подовжені біпіраміди[en] | Скручені подовжені біпіраміди[en] | ||||||
|---|---|---|---|---|---|---|---|---|
| J12(2М1) | Правильна | J13(2М3) | J14(М1+П3+М1) | J15(М2+П4+М2) | J16(М3+П5+М3) | Копланарна | J17(М2+А4+М2) | Правильні |
| Трикутна біпіраміда | Квадратна біпіраміда (октаедр) |
П'ятикутна біпіраміда | Подовжена трикутна біпіраміда | Подовжена чотирикутна біпіраміда | Подовжена п'ятикутна біпіраміда | Скручена подовжена трикутна біпіраміда (ромбоедр) |
Скручена подовжена чотирикутна біпіраміда | Скручена подовжена п'ятикутна біпіраміда (ікосаедр) |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
||
| Утворені з многогранників | ||||||||
| Тетраедр | Квадратна піраміда | П'ятикутна піраміда[en] | Тетраедр Трикутна призма |
Квадратна піраміда Куб |
П'ятикутна піраміда[en]П'ятикутна призма | Тетраедр Октаедр |
Квадратна піраміда Квадратна антипризма |
П'ятикутна піраміда[en] П'ятикутна антипризма |
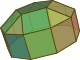
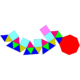
| Подовжені куполи[en] | Подовжена ротонда | Скручені подовжені куполи[en] | Скручена подовжена ротонда | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Копланарні | J18(М4+П6) | J19(М5+П8) | J20(М6+П10) | J21(М9+П10) | Увігнуті | J22(М4+А6) | J23(М5+А8) | J24(М6+А10) | J25(М9+А10) |
| Подовжений двосхилий купол | Подовжений трисхилий купол | Подовжений чотирисхилий купол | Подовжений п'ятисхилий купол | Подовжена п'ятисхила ротонда | Скручений подовжений двосхилий купол | Скручений подовжений трисхилий купол | Скручений подовжений чотирисхилий купол | Скручений подовжений п'ятисхилий купол | Скручена подовжена п'ятисхила ротонда |

|

|

|
|

|

|

|

|

|

|

|

|

|

|

|
|

|

| ||
| Утворені з многогранників | |||||||||
| Квадратна призма Трикутна призма |
Шестикутна призма Трисхилий купол |
Восьмикутна призма Чотирисхилий купол |
Десятикутна призма П'ятисхилий купол |
Десятикутна призма П'ятисхила ротонда |
Чотирикутна антипризма[en]Трикутна призма | Шестикутна антипризма Трисхилий купол |
Восьмикутна антипризмаЧотирисхилий купол | Десяткутна антипризма[en]П'ятисхилий купол | Десяткутна антипризма[en]П'ятисхила ротонда |
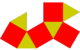
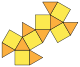
Повернуті трикутні бікуполи є напівправильними многогранниками (в цьому випадку — архімедовими тілами), тобто вони не належать до класу многогранників Джонсона.
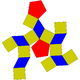
| Прямі куполи | Повернуті куполи | ||||||
|---|---|---|---|---|---|---|---|
| Копланарний | J27(2М4) | J28(2М5) | J30(2М6) | J26(П3+П3) | Напівправильний | J29(М5+М5) | J31(М6+М6) |
| Двосхилий прямий бікупол | Трисхилий прямий бікупол | Чотирисхилий прямий бікупол | П'ятисхилий прямий бікупол | Двосхилий повернутий бікупол (гіробіфастигіум) |
Трикутний повернутий бікупол (кубооктаедр) |
Чотирисхилий повернутий бікупол | П'ятисхилий повернутий бікупол |

|

|

|

|

|

|
||

|

|
|
|
|

|

| |
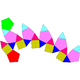
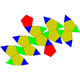
| Утворені з многогранників | |||||||
| Куполоротонди | Біротонди | ||
|---|---|---|---|
| J32(М6+М9) | J33(М6+М9) | J34(2М9) | Напівправильна |
| П'ятисхила пряма куполоротонда | П'ятисхила повернута куполоротонда | П'ятисхила пряма біротонда | П'ятисхила повернута біротонда (ікосододекаедр) |

|

|

|

|
|

|
|

|
| Утворені з многогранників | |||
| П'ятисхилий купол П'ятисхила ротонда |
П'ятисхила ротонда | ||
| Подовжені прямі бікуполи[en] | Подовжені повернуті бікуполи[en] | ||||||
|---|---|---|---|---|---|---|---|
| Копланарний | J35(М4+П6+М4) | Напівправильний | J38(М6+П10+М6) | Копланарний | J36(М4+П6+М4) | J37(М5+П8+М5) | J39(М6+П10+М6) |
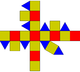
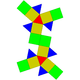
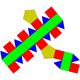
| Подовжений двосхилий прямий бікупол | Подовжений трисхилий прямий бікупол | Подовжений квадратний прямий бікупол (ромбокубооктаедр) |
Подовжений п'ятисхилий прямий бікупол | Подовжений двосхилий повернутий бікупол | Подовжений тисхилий повернутий бікупол | Подовжений чотирисхилий повернутий бікупол | Подовжений п'ятисхилий повернутий бікупол |

|

|

|

|

|

|

|

|

|
|

|
|

|
| ||
| Подовжені куполоротонди | Подовжені біротонди | ||
|---|---|---|---|
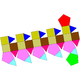
| J40(М6+П10+М9) | J41(М6+П10+М9) | J42(М9+П10+М9) | J43(М9+П10+М9) |
| Подовжена п'ятисхила пряма куполоротонда | Подовжена п'ятисхила повернута куполоротонда | Подовжена п'ятисхила пряма біротонда | Подовжена п'ятисхила повернута біротонда |

|

|

|

|

|
|

|

|
Кирпаті[en] антипризми можна побудувати альтеруванням зрізаних антипризм. Два тіла є многогранниками Джонсона, одне тіло правильне, а решту неможливо побудувати за допомогою правильних трикутників.
| Скручені подовжені бікуполи[en] | Скручена подовжена куполоротонда | Скручена подовжена біротонда | |||
|---|---|---|---|---|---|
| Неопуклі | J44(М4+А6+М4) | J45(М5+А8+М5) | J46(М6+А10+М6) | J47(М6+А10+М9) | J48(М9+А10+М9) |
| Скручений подовжений двосхилий бікупол | Скручений подовжений трисхилий бікупол | Скручений подовжений чотирисхилий бікупол | Скручений подовжений п'ятисхилий бікупол | Скручена подовжена п'ятисхила куполоротонда | Скручена подовжена п'ятисхила біротонда |

|

|

|

|

|

|

|

|

|

|

| |
| Утворені з многогранників | |||||
| Трикутна призма Квадратна антипризма |
Трисхилий купол Шестикутна антипризма |
Чотирисхилий купол Восьмикутна антипризма |
П'ятисхилий купол Десятикутна антипризма[en] |
П'ятисхилий купол П'ятисхила ротонда Десятикутна антипризма[en] |
П'ятисхила ротонда Десятиугольная антипризма[en] |
| J7(М1+ П3) (повторно) |
J49(П3+М2) | J50(П3+2М2) | J51(П3+3М2) | |
|---|---|---|---|---|
| Подовжена трикутна піраміда | Нарощена трикутна призма | Двічі нарощена трикутна призма | Тричі нарощена трикутна призма | |

|

|

|

| |

|

|

|

| |
| Утворені з многогранників | ||||
| Трикутна призма Тетраедр |
Трикутна призма Квадратна піраміда | |||
| Нарощені п'ятикутні призми | Нарощені шестикутні призми | ||||
|---|---|---|---|---|---|
| J52(П5+М2) | J53(П5+2М2) | J54(П6+М2) | J55(М2+П6+М2) | J56(П6+2М2) | J57(П6+3М2) |
| Нарощена п'ятикутна призма | Двічі нарощена п'ятикутна призма | Нарощена шестикутна призма | Двічі протилежно нарощена шестикутна призма | Двічі косо нарощена шестикутна призма | Тричі нарощена шестикутна призма |

|

|

|

|

|

|

|
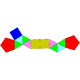
|

|
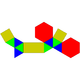
|

|

|
| Утворені з многогранників | |||||
| П'ятикутна призма Квадратна піраміда |
Шестикутна призма Квадратна піраміда | ||||
| Правильний | J58(М15+М3) | J59(М3+М15+М3) | J60(М15+2М3) | J61(М15+3М3) |
|---|---|---|---|---|
| Додекаедр | Нарощений додекаедр | Двічі протилежно нарощений додекаедр | Двічі косо нарощений додекаедр | Тричі нарощений додекаедр |

|

|

|

|

|

|

|
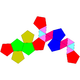
|
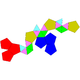
| |
| Утворені з многогранників | ||||
| Додекаедр і пятиугольная пирамида[en] | ||||
| Правильний | J11(М3+А5) (повторно) |
J62(М7+М3) | J63(М7) | J64(М7+М1) |
|---|---|---|---|---|
| Ікосаедр | Відсічений ікосаедр (Скручена подовжена п'ятикутна піраміда) |
Двічі косо відсічений ікосаедр | Тричі відсічений ікосаедр | Нарощений тричі відсічений ікосаедр |

|

|

|

|

|

|

|

|

| |
| Утворені з многогранників | ||||
| Тричі відсічений ікосаедр, пятиугольная пирамида[en] і тетраедр | ||||
| J65(М10+М4) | J66(М11+М5) | J67(М5+М11+М5) |
|---|---|---|
| Нарощений зрізаний тетраедр | Нарощений зрізаний куб | Двічі нарощений зрізаний куб |

|

|

|

|

|

|
| Утворені з многогранників | ||
| Зрізаний тетраедр Трисхилий купол |
Зрізаний куб Чотирисхилий купол | |
| Напівправильний | J68(М6+М12) | J69(М6+М12+М6) | J70(М12+2М6) | J71(М12+3М6) |
|---|---|---|---|---|
| Зрізаний додекаедр | Нарощений зрізаний додекаедр | Двічі протилежно нарощений зрізаний додекаедр | Двічі косо нарощений зрізаний додекаедр | Тричі нарощений зрізаний додекаедр |

|

|

|

|

|

|

|

|

|

|
| J72(М6+М14+М6=М6+М13+2М6) | J73(М6+М14+М6) | J74(2М6+М13+М6) | J75(3М6+М13) |
|---|---|---|---|
| Скручений ромбоікосододекаедр | Двічі протилежно скручений ромбоікосододекаедр | Двічі косо скручений ромбоікосододекаедр | Тричі скручений ромбоікосододекаедр |

|

|

|

|

|

|

|

|
| J76(М6+М14=2М6+М13) | J77(М14+М6) | J78(М13+М6+М6) | J79(М13+2М6) |
|---|---|---|---|
| Відсічений ромбоікосододекаедр | Протилежно скручений відсічений ромбоікосододекаедр | Косо скручений відсічений ромбоікосододекаедр | Двічі косо скручений відсічений ромбоікосододекаедр |

|

|

|

|
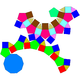
|

|

|

|
| J80(М14) | J81(М13+М6) | J82(М14+М6) | J83(М13) |
| Двічі протилежно відсічений ромбоікосододекаедр | Двічі косо відсічений ромбоікосододекаедр | Скручений двічі відсічений ромбоікосододекаедр | Тричі відсічений ромбоікосододекаедр |

|

|

|

|

|

|

|
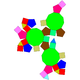
|
Кирпаті[en] антипризми можна побудувати альтеруванням зрізаних антипризм. Два тіла є многогранниками Джонсона, одне тіло правильне, а решту неможливо побудувати за допомогою правильних трикутників.
| J84(М25) | Правильний | J85(М28) | Неправильний |
|---|---|---|---|
| Тіло Джонсона | Правильний | Тіло Джонсона | Увігнутий… |
 Кирпатий двоклиноїд ss{2,4} |
 Ікосаедр ss{2,6} |
 Кирпата квадратна антипризма ss{2,8} |
 ss{2,10}… |

|

|

|
| J86(М22) | J87(М22+М3) | J88(М23) | |
|---|---|---|---|
| Клинокорона | Нарощена клинокорона | Велика клинокорона | |

|

|

| |

|

|

| |
| J89(М21) | J90(М24) | J91(М8) | J92(М20) |
| Сплощена велика клинокорона | Оперезаний двоклинник | Подвійна серпоротонда | Сплощена трикутна клиноротонда |

|

|

|

|

|

|

|
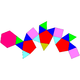
|
П'ять многогранників Джонсона є дельтаедрами, тобто, всі їх грані — правильні трикутники:
|
|
Двадцять чотири многогранники Джонсона мають тільки трикутні та чотирикутні грані:
Одинадцять тіл Джонсона мають тільки трикутні і п'ятикутні грані:
|
|
Вісім многогранників Джонсона мають тільки трикутні, квадратні і шестикутні грані:
|
|
П'ять многогранників Джонсона мають тільки трикутні, квадратні і восьмикутні грані:
|
|
25 многогранників Джонсона мають вершини, які лежать на одній сфері: 1-6, 11, 19, 27, 34, 37, 62, 63, 72-83. Всі ці многогранники можна отримати з правильних або однорідних многогранників шляхом повороту (купола) або відсікання (купола чи піраміди)[4].
| Октаедр | Кубооктаедр | Ромбокубооктаедр | |||
|---|---|---|---|---|---|
| J1(М2) |
J3(М4)
|
J27(2М4) | J4(М5)
|
J19(М5+П8)
|
J37(М5+П8+М5)
|
| Ікосаедр | Ікосододекаедр | ||||
|---|---|---|---|---|---|
| J2(М3)[en] |
J63(М7)
|
J62(М7+М3) | J11(М3+А5)
|
J6(М9)
|
J34(2М9)
|
J5(М6)
|
J76(М6+М14)
|
J80(М14)
|
J81(М13+М6)
|
J83(М13)
|
J72(М6+М14+М6)
|
J73(М6+М14+М6)
|
J74(2М6+М13+М6)
|
J75(3М6+М13)
|
J77(М14+М6)
|
J78(М13+М6+М6)
|
J79(М13+2М6)
|
J82(М14+М6)
|
- ↑ Pseudo Rhombicuboctahedra.
- ↑ Johnson N. W. Convex polyhedra with regular faces (preliminary report) // Notices Amer. Math. Soc. — 1960. — 16 червня. — С. 952.
- ↑ Залгаллер, 1967.
- ↑ Johnson solids et al.
- Гурин А. М. К истории изучения выпуклых многогранников с правильными гранями // Сиб. электрон. матем. изв. — 2010. — Т. 7 (16 июня). — С. A.5—A.23.
- Norman W. Johnson[en]. Convex Solids with Regular Faces // Canadian Journal of Mathematics. — 1966. — Т. 18 (16 червня). — С. 169—200. — ISSN 0008-414X. — DOI:. (Містить оригінальне перерахування 92 тіл і гіпотезу, що інших немає.)
- Залгаллер В. А. Выпуклые многогранники с правильными гранями. — М.—Л. : Наука, 1967. — Т. 2. — 221 с. — (Зап. научн. сем. ЛОМИ) (Перший доказ, що існує тільки 92 тел Джонсона.)
- Anthony Pugh. Глава 3. Дальнейшие выпуклые многогранники // Polyhedra: A visual approach. — California : University of California Press Berkeley, 1976. — ISBN 0-520-03056-7.
- Брёндстед А. Введение в теорию выпуклых многогранников. — М. : Мир, 1988.
- Sylvain Gagnon. «Convex многогранників with regular faces[недоступне посилання з листопада 2017]», Structural Topology. — 1982. — № 6. — P. 83-95.
- Paper Models of Многогранників Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W. Johnson Solid (англ.) на сайті Wolfram MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
- CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4 dimensional space
- Sylvain Gagnon. «Convex многогранників with regular faces[недоступне посилання з листопада 2017]». — Structural Topology. — 1982. — № 6. — P. 83-95.
- Паперові моделі многогранників Багато посилань
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W. Johnson Solid(англ.) на сайті Wolfram MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
- CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4-dimensional space