Локон Аньєзі

Локон Аньєзі — плоска крива третього порядку, геометричне місце точок , для яких виконується співвідношення ,
де — діаметр кола, — напівхорда цього кола, перпендикулярна до .
Свою назву "локон Аньєзі" крива отримала на честь італійської математикині Марії Гаетани Аньєзі, яка досліджувала цю криву.
Рівняння[ред. | ред. код]
,
- У декартовій системі координат:
Координати точки , що лежить на локоні — , . і за визначенням будуємо пропорцію
Звідси
З іншого боку може бути знайдений з рівняння кола:
Нам відомий , значить виражаємо :
Прирівнюємо обидва вирази для :
Зводимо в квадрат, переносимо та виносимо за дужки:
Виражаємо y (y=0 не підходить за визначенням):
- , де параметр — кут між і , приймає значення:
Координати точки однозначно визначаються кутом між і . Якщо , а , тоді за визначенням локону можна скласти пропорцію
за визначенням дорівнює . З трикутника : , значить
звідси . Цю формулу підставляємо в рівняння кривої:
Використавши тотожність, отримаємо
Раціональна параметризація для кривої має вигляд:
; параметр t приймає значення:
- У полярній системі рівняння локону досить складне: щоб його знайти, треба розв'язати кубічне рівняння:
Однак отримана формула буде занадто складною і невкладистою, щоб мати якесь практичне значення.
Властивості[ред. | ред. код]
- Локон Аньєзі — крива третього порядку.
- Діаметр єдина вісь симетрії кривої. Вісь Ох — її асимптота.
- Крива має один максимум — і дві точки перегину — . Вони лежать на прямих (кут ) [1] [2]
- В околі вершини локон наближається до кола діаметром . У точці відбувається дотик, і крива збігається з колом. Це показує значення радіуса кривини в точці : .
- Площа під графіком (між кривою і асимптотою): . [1] [2] [3] Вона обчислюється інтегруванням рівняння по всій числовій прямій [4], і дорівнює площі визначального круга, помноженій на 4.
Центр мас фігури, обмеженої кривою та її асимптотою лежить на осі симетріі, на відстані від асимптоти, тобто в точці з координатами [2]
Найбільший за площею прямокутник, який можна вписати між кривою та її асимптотою, має висоту, що дорівнює радіусу визначального кола, і ширину, що дорівнює подвоєному діаметру кола. Його площа: . [3]
- Об'єм тіла, утвореного обертанням кривої навколо своєї асимптоти (осі ): .[1] [2] . Цей об'єм вдвічі більше за об'єм тора, утвореного при обертанні визначального кола локона навколо цієї ж прямої.[3]
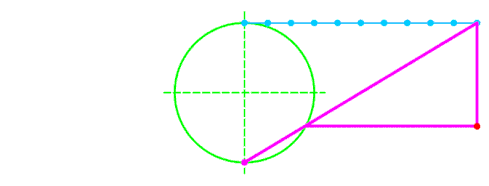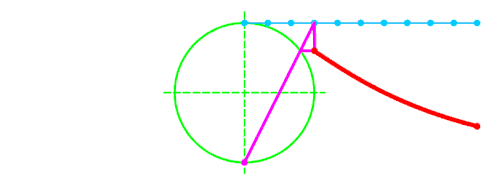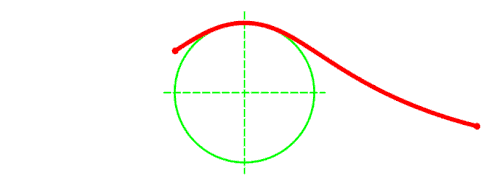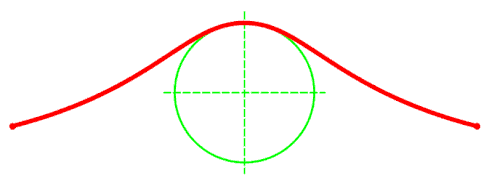
Побудова[ред. | ред. код]
- Будуємо коло діаметром і через нижню точку кола О проводимо дотичну Ox.
- Через верхню точку кола A (діаметрально протилежну до О) проводимо пряму, паралельну до Ох.
- Через точку О проводимо січну ОL, яка перетинає коло в точці C і верхню пряму в точці L.
- Через точку C проводимо пряму, паралельну до Ох, а через L проводимо пряму, паралельну до діаметра ОA. Ці дві прямі перетинаються в точці M, яка належить локону Аньєзі.
Споріднена крива[ред. | ред. код]
Крива, що носить назву "псевдо-локон" утворюється шляхом подвоєння ординат локона Аньєзі. Цю криву досліджував Дж. Грегорі в 1658 і використовував Готфрід Лейбніц у 1674 році, виводячи вираз: [2]
Див. також[ред. | ред. код]
Примітки[ред. | ред. код]
- ↑ а б в Lawrence, J. Dennis (2013), 4.3 Witch of Agnesi (Fermat, 1666; Agnesi, 1748), A Catalog of Special Plane Curves, Dover Books on Mathematics, Courier Corporation, с. 90—93, ISBN 9780486167664
- ↑ а б в г д Yates, Robert C. (1954), Witch of Agnesi, Curves and their Properties (PDF), Classics in Mathematics Education, т. 4, National Council of Teachers of Mathematics, с. 237—238
- ↑ а б в Larsen, Harold D. (January 1946), The Witch of Agnesi, School Science and Mathematics, 46 (1): 57—62, doi:10.1111/j.1949-8594.1946.tb04418.x
- ↑ Witch of Agnesi (PDF) (англ) .
{{cite web}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання)
Посилання[ред. | ред. код]
- Weisstein, Eric W. Witch of Agnesi(англ.) на сайті Wolfram MathWorld.
- Witch of Agnesi [Архівовано 8 грудня 2011 у Wayback Machine.] by Chris Boucher based on work by Eric W. Weisstein, The Wolfram Demonstrations Project.
- The Witch of Agnesi [Архівовано 7 червня 2011 у Wayback Machine.] - Mathforum.org Java applet
- Witch of Agnesi Encyclopedia of Mathematics.
- WITCH OF AGNESI - MATHCURVE.COM
- MacTutor History of Mathematics Archive. "Witch of Agnesi."
- Xah Lee. Witch of Agnesi
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||