Логарифм
| Логарифм | |
 | |
| Апроксимаційний алгоритм | CORDIC |
|---|---|
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
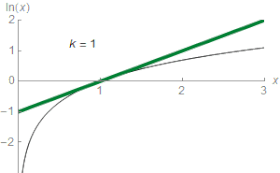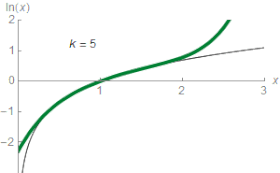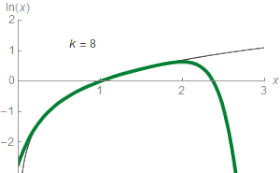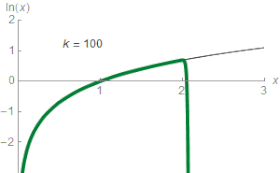 | |
| Протилежне | показникова функція |
| | |
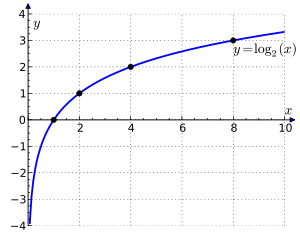
log2(2) = 1, тому що 21 = 2,
log2(4) = 2, тому що 22 = 4,
log2(8) = 3, тому що 23 = 8
Логари́фм, або логари́тм,[1][2] (від грец. λόγος — «слово», і грец. ἀριθμός — «число») — число (показник степеня, степінь), яке показує, до якого степеня слід піднести число (основу), щоб одержати число .
Основна логарифмічна тотожність: або , де , та .
Логарифми ввів Джон Непер на початку XVII століття як засіб спрощення розрахунків. Їх швидко почали застосовувати науковці та інженери для пришвидшення виконання обчислень із застосуванням логарифмічних лінійок і таблиць логарифмів. Логарифм дозволяє прискорити множення багатозначних чисел шляхом складання їхніх логарифмів. Наприклад, візьмімо два числа, які потрібно помножити: і . За допомогою таблиці логарифмів подивімося, що за основою ці числа мають логарифми (степені) і відповідно. Тобто, i . Таким чином, . Виходить, що логарифмом добутку чисел і , за основою , є число . З таблиці логарифмів легко знайти результат .
Сучасне означення логарифмів увів Леонард Ейлер, який у XVIII столітті пов'язав їх з показниковою функцією.
Позначення[ред. | ред. код]
Позначення:
- (логарифм числа за основою )
Існують особливі позначення для:
- натуральних логарифмів (логарифмів за основою e):
- десяткових логарифмів (логарифмів за основою 10):
- двійкових логарифмів (логарифмів за основою 2):
Логарифми були винайдені Джоном Непером на початку XVII століття як засіб для спрощення розрахунків і відтоді широко використовуються в науці, техніці. До винайдення комп'ютерів логарифмічна лінійка та таблиці логарифмів були повсякденним інструментом інженера.
Властивості[ред. | ред. код]
| Формула | Приклад | |
|---|---|---|
| Добуток | ||
| Частка | ||
| Степінь | ||
| Корінь |
Ці властивості зробили логарифм надзвичайно корисною функцією. Додавання та віднімання набагато простіші операції ніж множення та ділення, й, маючи таблицю логарифмів, можна сильно спростити складні обчислення.
Формула
дозволяє переходити від одної основи до іншої.
Інші тотожності:
Логарифмічна функція[ред. | ред. код]

Логарифмічна функція ставить у відповідність кожному значенню змінної її логарифм за наперед обраною основою .
Властивості логарифмічної функції:
- множина визначення логарифмічної функції ,
- логарифмічна функція є монотонною, причому
- є зростаючою, якщо
- є спадною, якщо
- логарифмічні функції за різними основами є пропорційними,
- функція є оберненою до показникової функції ,
- похідна логарифмічної функції:
- первісна логарифмічної функції:
- (див. також таблицю інтегралів логарифмічних функцій)
- похідна від логарифму функції називається логарифмічною похідною
- розклад у ряд Тейлора
Натуральні логарифми[ред. | ред. код]
Зв'язок з десятковим логарифмом: .
Як зазначено вище, для похідної натурального логарифму справедлива проста формула:
З цієї причини у математичних дослідженнях дуже часто використовують саме натуральні логарифми. Вони часто з'являються при розв'язку диференціальних рівнянь, дослідженні статистичних закономірностей (наприклад, розподіл простих чисел) тощо.
Невизначений інтеграл від натурального логарифму легко знайти інтегруванням за частинами:
Розклад у ряд Тейлора може бути представлений наступним чином:
при наступна рівність є справедливою
| (1) |
Зокрема,
Формула (1) не має великої практичної цінності через те, що ряд дуже повільно сходиться і значення є обмеженим у доволі вузькому діапазоні. Однак, не складно отримати з неї зручнішу формулу:
| (2) |
Цей ряд сходиться швидше, а крім цього, ліва частина формули тепер може виразити логарифм будь-якого додатного числа.
Двійкові логарифми[ред. | ред. код]
Логарифми за основою 2 широко застосовуються в теорії інформації. Двійковий логарифм натурального числа дозволяє визначити число цифр у внутрішньому комп'ютерному (бітовому) поданні цього числа:
- (дужки позначають цілу частину числа).
Інформаційна ентропія — міра кількості інформації, також заснована на двійкових логарифмах.
Оцінка асимптотичної складності рекурсивних алгоритмів, заснованих на принципі «розділяй та володарюй» — таких, як швидке сортування, швидке перетворення Фур'є, двійковий пошук виконується з використанням двійкових логарифмів.
У теорії музики, щоб вирішити питання про те, на скільки частин ділити октаву, потрібно відшукати раціональне наближення для Якщо розкласти це число в безперервний дріб, то третій дріб, що підходить, (7/12) дозволяє обґрунтувати класичний розподіл октави на 12 півтонів.
Десяткові логарифми[ред. | ред. код]


Логарифми за основою 10 (позначаються як lg a) до винайдення калькуляторів широко використовувалися для обчислень. Нерівномірна шкала десяткових логарифмів зазвичай наноситься і на логарифмічні лінійки. Подібна шкала використовується у багатьох областях науки, наприклад:
- Фізика — інтенсивність звуку (децибели).
- Астрономія — шкала яскравості зірок.
- Хімія — активність водневих іонів (pH).
- Сейсмологія — шкала Ріхтера.
- Теорія музики — нотна шкала, по відношенню до частот нотних звуків.
- Історія — логарифмічна шкала часу.
Логарифмічна шкала також широко використовується для виявлення показника степеня у показникових залежностях і коефіцієнта у показнику експоненти. При цьому графік, побудований у логарифмічному масштабі по одній або двох осях, приймає вигляд прямої, яка є простішою для дослідження.
Логарифмічна функція комплексної змінної[ред. | ред. код]
Визначення і властивості[ред. | ред. код]
Для комплексних чисел логарифм визначається так само як і для дійсних. На практиці використовується майже завжди натуральний комплексний логарифм, який позначимо як і визначимо як множину всіх комплексних чисел таких, що . Комплексний логарифм існує для будь-якого , і його дійсна частина визначається однозначно, тоді як уявна частина має нескінченну множину значень. З цієї причини його називають багатозначною функцією. Якщо представити у показниковій формі:
- ,
то логарифм знаходиться за формулою:
Тут — дійсний логарифм, , — довільне ціле число. Значення, що отримуємо при , називається головним значенням комплексного натурального логарифму; прийнято брати значенням аргументу у ньому в інтервалі . Відповідна (вже однозначна) функція називається головною гілкою логарифму і позначається . Інколи через також позначають значення логарифму, що лежить не на головній гілці.
З формули маємо наступні наслідки:
- Дійсна частина логарифму визначається за формулою:
- Логарифм від'ємного числа знаходиться за формулою:
Оскільки комплексні тригонометричні функції пов'язані з експонентою (формула Ейлера), то комплексний логарифм як функція, що обернена до експоненти, пов'язаний з оберненими тригонометричними функціями. Приклад такого зв'язку:
Приклади[ред. | ред. код]
Наведемо головне значення логарифму для деяких аргументів:
Потрібно бути обережним при перетвореннях комплексних логарифмів, беручи до уваги, що вони багатозначні, тому з рівності логарифмів будь-яких виразів не виходить рівність цих виразів. Приклад помилкових міркувань:
- — неправильно (суперечність).
Відзначимо, що зліва стоїть головне значення логарифма, а справа — значення з нижчої гілки (). Причина помилки — неправильне використання властивості , яка, загалом, справджується у випадку комплексних чисел для всього нескінченного набору значень логарифма, а не тільки для головного значення.
Аналітичне продовження[ред. | ред. код]

Логарифм комплексного числа також може бути визначений як аналітичне продовження дійсного логарифму на всю комплексну площину. Нехай крива починається в одиниці, не проходить через нуль і не перетинає від'ємну частину дійсної осі. Тоді головне значення логарифму в кінцевій точці кривої можна визначити за формулою:
Якщо — проста крива (без самоперетину), то для чисел, що лежать на ній, логарифмічні тотожності можна застосовувати без обмежень, наприклад
Якщо дозволити кривій перетинати від'ємну частину дійсної осі, то перший такий перетин переносить результат з гілки головного значення на сусідню гілку, а кожен наступний перетин викликає аналогічне зміщення по гілках логарифмічної функції (дивіться рисунок).
Із формули аналітичного продовження виходить, що на будь-якій гілці логарифму
Для будь-якого околу , що містить точку :
Інтеграл береться у додатному напрямку (проти годинникової стрілки). Ця тотожність лежить в основі теорії лишків.
Можна також визначити аналітичне продовження комплексного логарифма за допомогою ряду, що наведений вище (1), і який узагальнений для випадку комплексного аргументу. Однак із вигляду розкладу в ряд маємо наслідок, що він дорівнює нулю в одиниці, тобто ряд відноситься лише до головної гілки багатозначної функції комплексного логарифма.
Поверхня Рімана[ред. | ред. код]
Комплексна логарифмічна функція — приклад поверхні Рімана; її уявна частина (рисунок 3) складається з нескінченного числа гілок, що закручені у вигляді спіралі. Ця поверхня однозв'язна; єдиний її нуль (першого порядку) отримуємо при , особливі точки: і (точки розгалуження нескінченного порядку).
Ріманова поверхня логарифму є універсальним накриттям для комплексної площини без точки .
Історія[ред. | ред. код]
Ще у VIII столітті індійський математик Вірасена розвинув концепцію ардхакчеди, що означала скільки разів число виду 2n можна поділити на два. Для чисел, які не є цілими степенями двійки ардхакчеда залишалася невизначеною. Він описав також трікачеду та чатуртхачеду — відповідні числа для основ 3 і 4[3][4]. 1544 року Міхаель Штифель опублікував у Нюрнбергу книгу Arithmetica integra з таблицею[5] цілих чисел і степенів двійки, які їм відповідають[6][7]. Ці ранні дослідження можна вважати попередниками логарифмів.

Метод логарифмування був опублікований Джоном Непером у 1614 році в книзі під назвою Mirifici Logarithmorum Canonis Descriptio (Опис чудового правила логарифмів)[8]. Незалежно від Непера логарифми відкрив Юст Бурґі, але його публікація з'явилася на 6 років пізніше[9].
Непер не тільки сформулював правило множення чисел з використанням логарифмів, а й побудував перші логарифмічні таблиці. Методом повторного віднімання Непер обрахував 107(1 − 10−7)L для L від 1 до 100. Для L=100 результат приблизно дорівнює 0.99999 = 1 − 10−5. Далі він порахував добутки цих чисел при множенні на 107(1 − 10−5)L для L від 1 до 50, і, аналогічно, добутки цих чисел при множенні на 0.9995 ≈ (1 − 10−5)20 й 0.99 ≈ 0.99520. Обчислення тривали 20 років. Як наслідок він отримав число L, яке є розв'язком рівняння
для чисел від 5 до 10 000 000.
Спочатку Непер назвав L штучним числом, але потім запровадив новий термін — логарифм. У сучасній нотації з використанням натуральних логарифмів це співвідношення має вигляд[10]
де наближення відповідає тому, що
з дуже малою похибкою.
Дуже швидко винахід Непера здобув широке визнання. Роботи італійця Бонавентури Кавальєрі та німця Йоганна Кеплера розвинули і вдосконалили концепцію[11]. 1620 року Едмунд Вінґейт збудував першу логарифмічну лінійку.
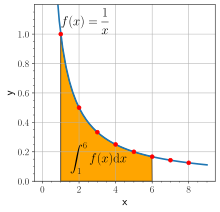
1647 року Грегуар де Сент-Вінсент отримав зв'язок між логарифмом та квадратурою гіперболи, зауваживши, що площі під графіком функції y = 1/x між 1 та числами a та b задовольняють співвідношенню:
- .
Натуральні логарифми були вперше описані Нікола Меркаром у праці Logarithmotechnia 1668 року[12], хоча ще у 1619 вчитель математики Джон Спейделл складав таблицю натуральних логарифмів[13].
Приблизно 1730 року Леонард Ейлер дав означення експоненти та натурального логарифма як
Ейлер показав, що ці функції обернені одна одній[14][15][16].
Деякі практичні застосування[ред. | ред. код]
Логарифмічна лінійка[ред. | ред. код]


Логарифмі́чна лінійка — аналоговий обчислювальний пристрій, що дозволяє виконувати кілька математичних операцій, основними з яких є множення і ділення чисел.
Найпростіша логарифмічна лінійка складається з двох шкал у логарифмічному масштабі, що здатні пересуватися одна відносно одної. Складніші лінійки містять додаткові шкали і прозорий повзунок з кількома поділками. На зворотній стороні лінійки можуть знаходитися різні довідкові матеріали.
За допомогою додаткових шкал можна здійснювати піднесення до степеня (частіше всього до квадрата і куба), обчислення логарифмів, тригонометричних функцій та обернених операцій (добування квадратних і кубічних коренів, обчислення експоненти та обернених тригонометричних функцій), перетворення величин між різними системами (наприклад, кіловатів на кінські сили чи навпаки) та деякі інші операції.
Принцип дії[ред. | ред. код]
Основний принцип дії логарифмічної лінійки заснований на тому, що множення і ділення чисел замінюється відповідно додаванням і відніманням їх логарифмів:
- lg (xy) = lg x + lg y,
- lg (x/y) = lg x − lg y.
Для того щоб обчислити добуток двох чисел, початок (чи кінець) рухомої шкали суміщують із першим множником на нерухомій шкалі, а на рухомій шкалі відшукують другий множник. Напроти нього на нерухомій шкалі знаходиться результат множення чисел.
Щоб розділити числа, на рухомій шкалі знаходять дільник і суміщують його з діленим на нерухомій шкалі. Початок (або кінець) рухомої шкали вказує на результат.
За допомогою логарифмічної лінійки знаходять лише мантису числа, його порядок обчислюється усно. Точність обчислення звичайних логарифмічних лінійок — два-три десяткових знаки. Для виконання інших операцій застосовують повзунок та додаткові шкали. Слід відзначити, що, незважаючи на простоту, на логарифмічній лінійці можна виконувати досить складні розрахунки.
Історія[ред. | ред. код]
Перший варіант лінійки розробив англійський математик-аматор Вільям Отред 1622 року.
Раніше випускалися посібники з їх використання досить великого обсягу[17][18].
В СРСР логарифмічні лінійки широко застосовувалися для виконання інженерних розрахунків приблизно до початку 80-х років XX століття, коли їх було витіснено калькуляторами.

Відродження логарифмічної лінійки відбулося на початку XXI сторіччя внаслідок попиту на наручні годинники та хронометри із вбудованим простим обчислювальним пристроєм. Його виконано у вигляді двох логарифмічних шкал навколо циферблату годинника, одна з яких може обертатися (базель). За примхою виробників такі пристрої зазвичай називають «навігаційна лінійка». За допомогою такого пристрою можна виконувати переведення миль на кілометри, літрів на галони, метри за секунду в кілометри за годину тощо[19]. На відміну від калькулятора одразу будується таблиця відповідності величин.
Прикладом таких годинників можна вважати Breitling Navitimer, CITIZEN (моделі BJ7010-59E, JQ8005-56E, JR3130-55E), Orient (моделі OCEM58002DV, OCTD09001B, OCTD09003D) та деякі інші.
Логарифмічна спіраль[ред. | ред. код]


Логарифмічна спіраль або ізогональна спіраль — особливий вид спіралі, що часто зустрічається в природі. Логарифмічна спіраль була вперше описана Декартом і пізніше інтенсивно досліджена Бернуллі, який називав її Spira mirabilis — «дивовижна спіраль». Власне термін «логарифмічна спіраль» (фр. spirale logarithmique) першим вжив П'єр Варіньон[20]
Рівняння[ред. | ред. код]
У полярних координатах рівняння кривої може бути записано як
або
що пояснює назву «логарифмічна».
У параметричній формі його може бути записано як
де a, b — дійсні числа.
Властивості[ред. | ред. код]
- Кут, що утворюється дотичною в довільній точці логарифмічної спіралі з радіус-вектором точки дотику, постійний і залежить лише від параметра
- У термінах диференціальної геометрії це може бути записано як
- У термінах диференціальної геометрії це може бути записано як
- Похідна функції пропорційна параметру b. Іншими словами, він визначає, наскільки щільно і в якому напрямку закручується спіраль. У граничному випадку, коли спіраль вироджується в коло радіусу a. Навпаки, коли b прямує до нескінченності спіраль наближається до прямої лінії. Кут, що доповнює до 90 °, називають нахилом спіралі.
- Розмір витків логарифмічної спіралі поступово збільшується, але їх форма залишається незмінною. Можливо, внаслідок цієї властивості, логарифмічна спіраль з'являється в багатьох зростаючих формах, подібних до мушлель молюсків і квіток соняшників.
-
Мушля молюска Наутілуса за формою близька до логарифмічної спіралі
-
Область низького тиску над Ісландією
-
Секція множини Мандельброта, що є логарифмічною спіраллю
Примітки[ред. | ред. код]
- ↑ Revue statistique de l'Ukraine (українською) . 1928.
- ↑ Fizychniĭ zbirnyk (рос.). Vyd-vo Lʹvivsʹkoho derz︠h︡. universytetu. 1959.
- ↑ Gupta, R. C. (2000), History of Mathematics in India, у Hoiberg, Dale; Ramchandani (ред.), Students' Britannica India: Select essays, New Delhi: Popular Prakashan, с. 329, архів оригіналу за 17 березня 2018, процитовано 22 червня 2011
{{citation}}:|editor3-first=з пропущеним|editor3-last=(довідка) - ↑ Dr. Hiralal Jain, ред. (1996), THE SHATKHANDAGAMA OF PUSHPADANTA AND BHOOTABAL (вид. 3rd), Solapur: Jain Samskriti Samrakshaka Sangha, архів оригіналу за 11 травня 2011, процитовано 22 червня 2011
{{citation}}: Проігноровано невідомий параметр|unused_data=(довідка), part 3-4-5, book 4 - ↑ Stifelio, Michaele (1544), Arithmetica Integra, London: Iohan Petreium, архів оригіналу за 22 червня 2013, процитовано 22 червня 2011
- ↑ Bukhshtab, A.A.; Pechaev, V.I. (2001), Arithmetic, у Hazewinkel, Michiel (ред.), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
- ↑ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart and Winston, с. 182, ISBN 978-0-03-077670-0, архів оригіналу за 12 вересня 2019, процитовано 22 червня 2011
- ↑ Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ↑ Boyer 1991, Chapter 14, section "Jobst Bürgi"
- ↑ William Harrison De Puy (1893), The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, т. 17 (вид. 9th), Werner Co., с. 179, архів оригіналу за 12 вересня 2019, процитовано 22 червня 2011
- ↑ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, section 2
- ↑ J. J. O'Connor; E. F. Robertson (2001-09), The number e, The MacTutor History of Mathematics archive, архів оригіналу за 11 лютого 2012, процитовано 02/02/2009
- ↑ Cajori, Florian (1991), A History of Mathematics (вид. 5th), Providence, RI: AMS Bookstore, ISBN 978-0-8218-2102-2, архів оригіналу за 12 вересня 2019, процитовано 22 червня 2011, p. 152
- ↑ Maor, Eli (2009), e: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, sections 1, 13
- ↑ Eves, Howard Whitley (1992), An introduction to the history of mathematics, The Saunders series (вид. 6th), Philadelphia: Saunders, ISBN 978-0-03-029558-4, section 9-3
- ↑ Boyer, Carl B. (1991), A History of Mathematics, New York: John Wiley & Sons, ISBN 978-0-471-54397-8, p. 484, 489
- ↑ Панов Д.Ю. Счетная линейка. — 21-е изд. — М : Наука, 1973. — 168 с.(рос.)
- ↑ Богомолов Н.В. Практические занятия с логарифмической линейкой (сборник задач). — М : Высшая школа, 1977. — 103 с.(рос.)
- ↑ Citizen BJ7010-59E. Watch Zone. Архів оригіналу за 30 червня 2013. Процитовано 2 листопада 2010.
- ↑ Spirale logarithmique. [Архівовано 29 червня 2012 у Wayback Machine.] (фр.)
Див. також[ред. | ред. код]
Література[ред. | ред. код]
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- Сторчай, Володимир Федорович. Показникові і логарифмічні рівняння: навч. посібник / В. Ф. Сторчай ; Дніпропетровський держ. ун-т. — К. : [б.в.], 1995. — 100 с
- Щербинин, Гарий Петрович. Показательно- логарифмические выражения, уравнения и неравенства: учеб. пособие / Г. П. Щербинин, Т. А. Недзельская ; ИСИО, Харьковский гос. технический ун-т радиоэлектроники. — Х. : [б.в.], 1995. — 60 с.
- Барановська, Галина Григорівна. Практикум з математики: Показникова та логарифмічна функції: навч. посібник для вступників до вузів / Г. Г. Барановська, В. В. Ясінський ; Національний технічний ун-т України «Київський політехнічний ін-т». Факультет довузівської підготовки. — К. : [б.в.], 1998. — 124 с.
- Кушнір, Ісаак. У світі логарифмів. — К. : Факт, 2004. — 136 с.: рис.
Посилання[ред. | ред. код]
- Функція логарифмічна // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
| Вікіцитати містять висловлювання на тему: Логарифм |
- Логарифмічна функція // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 179. — 594 с.
- Динамічні математичні моделі FIZMA.neT [Архівовано 13 вересня 2021 у Wayback Machine.]
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
|





























![{\displaystyle \log _{a}{\sqrt[{p}]{x}}={\frac {1}{p}}\log _{a}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b40486767b64c5e22cc9dbfcfd6621cf68f71a88)
















![{\displaystyle \gamma =\lim _{n\rightarrow \infty }\left[\left(\sum _{k=1}^{n}{\frac {1}{k}}\right)-\ln(n)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7af12010d95e43a1b424a6c3a76c92c2727c1c06)























![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)







































