Динамічна система

Динамі́чна систе́ма — математична абстракція, призначена для опису і вивчення систем, що еволюціонують з часом. Прикладом можуть служити механічні системи (рухомі групи тіл) або фізичні процеси.
Динамічні системи досліджує теорія динамічних систем, яка має застосування в широкому переліку областей, як от математика, фізика,[1][2], біологія,[3] хімія, інженерія,[4] економіка,[5] історія та медицина. Динамічні системи є основою для теорії хаосу, динамік логістичних відображень, теорії біфуркацій, процесів самозбирання і самоорганізації та концепції границі хаосу.
Огляд[ред. | ред. код]
Концепція динамічних систем походить з класичної механіки. Там, як і в інших природничих та інженерних дисциплінах, правило еволюції динамічних систем є неявним співвідношенням, яке задає стан системи лише на короткий час у майбутньому. (Це співвідношення задається через диференціальні рівняння, рекурентні співвідношення, тощо.) Щоб визначити стан для всіх майбутніх миттєвостей часу, потрібно повторити співвідношення для кожного просування на невеликий крок. Ця ітераційна процедура називається розв'язанням системи або інтегруванням системи. Якщо систему можна розв'язати, то за початковою точкою можна визначити всі її майбутні положення—сукупність точок, яку називають траєкторією або орбітою[en].
До появи комп'ютерів пошук орбіти вимагав складних математичних обчислень та міг бути здійснений лише для невеликого класу динамічних систем. Чисельні методи, реалізовані на електронно-обчислювальних машинах, спростили задачу визначення орбіт динамічної системи.
Для простих динамічних систем часто достатньо знати траєкторію, але більшість динамічних систем занадто складні, щоб їх розуміти в якості окремих траєкторій. Труднощі виникають через:
- Системи, що вивчаються, можуть бути відомі лише приблизно — параметри системи можуть бути не відомі точно або бути відсутніми в рівняннях. Використані наближення ставлять під сумнів вірність чи релевантність чисельних розв'язків. Для вирішення цих питань у дослідження динамічних систем було введено кілька понять стабільності, наприклад стійкість за Ляпуновим або структурна стійкість. Стійкість динамічної системи означає, що існує клас моделей або початкових умов, для яких траєкторії будуть еквівалентними. Операції порівнянь орбіт для встановлення їх еквівалентності різні для різних понять стійкості.
- Тип траєкторії може бути важливішим, ніж одна конкретна траєкторія. Деякі траєкторії можуть бути періодичними, тоді як інші можуть блукати через багато різних станів системи. Застосування часто вимагають перерахування цих класів або підтримки системи в межах одного класу. Класифікація всіх можливих траєкторій привела до якісного вивчення динамічних систем, тобто властивостей, які не змінюються при зміні координат. Лінійні динамічні системи та системи, які мають два числа, що описують стан, є прикладами динамічних систем, де зрозумілі можливі класи орбіт.
- Поведінка траєкторій як функція від параметра може бути тою, що потрібна для застосування. Оскільки параметр змінюється, динамічні системи можуть мати точки біфуркації, в яких змінюється якісна поведінка динамічної системи. Наприклад, вона може перейти від лише періодичних рухів до явно непостійної поведінки, як при переході до турбулентності рідини.
- Траєкторії системи можуть здаватися непостійними, ніби випадковими. У цих випадках може знадобитися обчислити середні значення, використовуючи одну дуже довгу траєкторію або багато різних траєкторій. Середні значення добре визначені для ергодичних систем, а для гіперболічних систем було розроблено більш детальне розуміння. Розуміння імовірнісних аспектів динамічних систем допомогло встановити основи статистичної механіки та хаосу.
Історія[ред. | ред. код]
Багато людей вважають французького математика Анрі Пуанкаре засновником теорії динамічних систем.[6] Пуанкаре опублікував дві вже класичні монографії «Нові методи небесної механіки» (1892—1899) та «Лекції з небесної механіки» (1905—1910). У них він успішно дослідив задачу про рух трьох тіл та детально вивчив поведінку розв'язків. Ці роботи включали теорему Пуанкаре про рекурентність[en], яка стверджує, що деякі системи через досить тривалий, але скінченний час повертаються до стану, дуже близького до початкового.
Олександр Ляпунов розробив багато важливих методів апроксимації. Його методи, розроблені ним у 1899 р., дозволяють визначити стійкість розв'язків звичайних диференціальних рівнянь. Він створив сучасну теорію стійкості динамічних систем.
У 1913 році американський математик Джордж Девід Біркгоф довів останню теорему Пуанкаре[en], окремий випадок задачі трьох тіл, цей результат зробив його всесвітньо відомим. У 1927 році він опублікував роботу Динамічні системи [Архівовано 6 грудня 2006 у Wayback Machine.]. Також відомими результатом Біркгофа стало його відкриття в 1931 році того, що зараз називають ергодичною теоремою. Поєднуючи знання з фізики щодо ергодичної гіпотези з теорією міри, за допомогою цієї теореми було вирішено фундаментальну проблему статистичної механіки. Ергодична теорема також мала вплив на динаміку.
Інший американський математик Стівен Смейл також досяг значних успіхів. Його першим внеском стала підкова Смейла, яка дала початок значним дослідженням динамічних систем. Він також окреслив дослідницьку програму, яку проводили багато інших вчених.
У 1964 році український математик Олександр Шарковський довів теорему про періоди дискретних динамічних систем. Одним із наслідків цієї теореми є те, що якщо дискретна динамічна система на дійсній прямій має періодичну точку періоду 3, то вона також має періодичні точки кожного іншого періоду.
Наприкінці 20 століття почали набувати популярність динамічні системи, пов'язані з диференціальними рівняннями з частинними похідними. Палестинський інженер-механік Алі Х. Найфе[en] застосував нелінійну динаміку в механічних та інженерних системах.[7] Його піонерська робота в галузі прикладної нелінійної динаміки мала вплив на будівництво та обслуговування машин та конструкцій, які є звичайними в повсякденному житті, таких як кораблі, крани, мости, будівлі, хмарочоси, реактивні двигуни, ракетні двигуни, літаки та космічні апарати.[8]
Основні поняття[ред. | ред. код]
Нехай — топологічний простір та — неперервна функція, яка задовольняє наступні умови:
- 1) для довільного , тобто ;
- 2) для довільних (групова властивість).
Тоді однопараметрична сім'я відображень , де , називається неперервною (або топологічною) динамічною системою.
Топологічний простір називається фазовим простором динамічної системи.
Відображення називається рухом точки , а його графік — траєкторією точки .
Орбітою точки називається множина . Множина називається додатною напів орбітою точки , а — від'ємною напів орбітою точки .
Підмножина фазового простору називається інваріантною (відповідно додатно-напівінваріантною, від'ємно-напівінваріантною), якщо для довільного (відповідно ) .
Існує два види визначень динамічних систем: перший мотивується звичайними диференціальними рівняннями і має геометричний характер, а інший — ергодичною теорією і має мірний характер.
Геометричне визначення[ред. | ред. код]
У геометричному визначенні є многовидом або графом у дискретному випадку, а — правило еволюції таке що, є дифеоморфізмом многовиду самого в себе. Тому є «гладким» відображенням часової області в простір дифеоморфізмів многовиду самого в себе.
Динамічні системи з неперервним часом[ред. | ред. код]
Для дійсної динамічної системи, динамічної системи дійсного часу, динамічної системи з неперервним часом або потоку визначається многовидом, локально дифеоморфним деякому Банаховому простору. Якщо неперервно диференційована функція, то динамічну систему називають диференційованою. Якщо многовид локально дифеоморфний , то динамічну систему називають скінченновимірною, інакше — нескінченновимірною. Коли визначена на всій дійсній прямій для всіх , то динамічну систему називають глобальною або потоком[en], а коли на додатній півосі, то — напівпотоком.
Динамічні системи з дискретним часом[ред. | ред. код]
Для дискретної динамічної системи або динамічної системи з дискретним часом визначається многовидом, локально дифеоморфним деякому Банаховому простору. Коли визначена лише на цілих числах для всіх , то динамічну систему називають каскадом або відображенням, а коли на невід'ємних цілих, то — напівкаскадом.[9]
Компактифікація динамічної системи[ред. | ред. код]
Нехай задано потік на локально компактному та гаусдорфовому топологічному просторі . Часто корисно вивчати неперервне розширення до для одноточкової компактифікації до . Хоч буде втрачена диференціальна структура вихідної системи, але можна буде використовувати компактність для аналізу нової динамічної системи, бо у компактній системі, як мінімум, гранична множина кожної орбіти є непорожньою, компактною та однозв'язною областю.
Мірне визначення[ред. | ред. код]
Динамічну систему можна визначити як перетворення, що зберігають міру, для мірного простору[en]. Нехай — мірний простір[en], де — непорожня множина, — сигма-алгебра на , — скінченна міра на , а — -вимірна функція. Кажуть, що відображення зберігає міру тоді і тільки тоді, коли для кожного виконується рівність . Поєднуючи вищесказане, кажуть, що відображення є перетворенням , що зберігає міру, якщо це відображення з на себе є -вимірним і зберігає міру, а сім'ю — динамічною системою, що зберігає міру.
Зв'язок з геометричним визначенням[ред. | ред. код]
Мірне визначення передбачає існування перетворення, що зберігає міру. Багато різних інваріантних мір можуть бути пов'язані з будь-яким одним правилом еволюції. Якщо динамічна система задана системою диференціальних рівнянь, то необхідно визначити відповідну міру. Це ускладнює розробку ергодичної теорії, починаючи з диференціальних рівнянь, тому стає зручним мати в ергодичній теорії визначення, мотивоване динамічними системами, яке обходить стороною вибір міри та припускає, що вибір зроблено. Проста конструкція (іноді її називають теоремою Крилова — Боголюбова) показує, що для великого класу систем завжди можна побудувати міру так, щоб зробити правило еволюції динамічної системи перетворенням, що зберігає міру.
Для гіперболічних динамічних систем природним вибором є міра Синая — Рюелля — Бовена[en]. Вона будується на геометричній структурі стійкого або нестійкого многовиду[en] динамічної системи; вона поводяться фізично при невеликих збуреннях та пояснює багато спостережуваної статистики гіперболічних систем.
Побудова динамічних систем[ред. | ред. код]
Для задання динамічної системи необхідно описати її фазовий простір, множину моментів часу і деяке правило, що описує рух точок фазового простору з часом. Концепція еволюції в часі є центральною в теорії динамічних систем, як показано в попередніх розділах: основною причиною цього факту є те, що початковою мотивацією теорії було вивчення часової поведінки класичних механічних систем. Але систему звичайних диференціальних рівнянь необхідно розв'язати, перш ніж вона стане динамічною системою. Наприклад, розглянемо таку задачу Коші:
де
- являє собою швидкість матеріальної точки x
- є скінченновимірним многовидом
- є вектор-функцією в або та являє собою зміну швидкості, викликану силами, що діють на дану матеріальну точку у фазовому просторі . Ця зміна не є вектором у фазовому просторі , але є вектором дотичному просторі .
Немає потреби ні в похідних вищого порядку в рівнянні, ні в параметрі у , оскільки їх можна усунути, розглянувши системи вищих розмірностей.
Залежно від властивостей цієї вектор-функції механічну систему називають
- автономною, якщо ;
- однорідною, якщо для всіх .
Рішення можна знайти за допомогою стандартних методів розв'язання однорідних диференціальних рівнянь та позначається як функція еволюції, вже введена вище
Після наступних маніпуляцій:
де — функціонал з множини еволюційних функцій до поля комплексних чисел, отримаємо більш загальний вигляд рівнянь, яким повинна задовольняти динамічна система.
Це рівняння корисне при моделюванні механічних систем зі складними обмеженнями.
Багато концепцій динамічних систем можна поширити на нескінченновимірні многовиди, які є локально банаховими просторами. У цьому випадку диференціальні рівняння є диференціальними рівняннями з частинними похідними.
Приклади[ред. | ред. код]
- Відображення кота Арнольда[en]
- Відображення пекаря[en] є прикладом хаотичного кусково-лінійного відображення
- Більярд[en] та зовнішній більярд[en]
- Динаміка підстрибування м'яча[en]
- Відображення кола
- Комплексний квадратний поліном[en]
- Подвійний маятник
- Діадичне перетворення[en]
- Відображення Хенона
- Ірраціональне обертання[en]
- Відображення Каплана-Йорка[en]
- Система Лоренца
- Відображення Ресслера[en]
- Коливальна машина Атвуда[en]
- Відображення тент[en]
Лінійні динамічні системи[ред. | ред. код]
У лінійній динамічній системі фазовий простір є n-вимірним евклідовим простором, тому будь-яка точка фазового простору може бути представлена вектором з n чисел. Аналіз лінійних систем можливий тому, що вони задовольняють принцип суперпозиції: якщо та задовольняють диференціальне рівняння для вектор-функції (але не обов'язково початковій умові), то і задовольняє це рівняння.
Потоки[ред. | ред. код]
Для потоку[en] вектор-функція є афінною функцією положення у фазовому просторі, тобто
де — матриця, — вектор констант та — вектор положення. Розв'язок цієї системи можна знайти за допомогою принципу суперпозиції (лінійності). Випадок з — це просто пряма з напрямком b:
- .
Коли та , початок координат є точкою рівноваги (або сингулярною точкою) потоку, тобто якщо , то орбіта залишається там. Для інших початкових умов рівняння руху задається експонентою від матриці. Тобто, для початкової точки матимемо:
- .
Коли , то власні значення визначають структуру фазового простору. З власних значень і власних векторів можна визначити: збіжиться чи розбіжиться початкова точка до точки рівноваги в початку координат.
Відстань між двома різними початковими умовами при у більшості випадків змінюватиметься експоненційно — або сходячись експоненційно швидко до точки, або розходячись експоненційно швидко. Лінійні системи демонструють чутливу залежність від початкових умов у разі розбіжності. Для нелінійних систем це одна з (необхідних, але не достатніх) умов хаотичної поведінки.
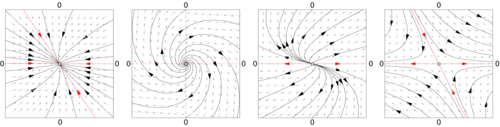
Каскади[ред. | ред. код]
Афінна динамічна система з дискретним часом задається наступним матричним різницевим рівнянням[en]:
- ,
з матрицею A та вектором b. Як і в неперервному випадку, заміна координат вилучає вільний член b з рівняння. У новій системі координат початок координат є нерухомою точкою відображення, а розв'язки лінійної системи — . Розв'язком вже є не криві, а точки, які стрибають у фазовому просторі. Орбіти організовані у вигляді кривих, або волокон, які представляють собою сукупність точок, які відображаються в самих себе під дією відображення.
Як і в неперервному випадку, власні значення та власні вектори A визначають структуру фазового простору. Наприклад, якщо є власним вектором A з дійсним власним значенням, меншим за одиницю, то пряма лінія, задана точками , де , є інваріантною кривою каскаду. Точки на цій прямій переходять у нерухому точку.
Існує також багато інших дискретних динамічних систем[en].
Локальна динаміка[ред. | ред. код]
Якісні властивості динамічних систем не змінюються при гладкій зміні координат (це іноді приймають як визначення якісного): особлива точка вектор-функції (точка, де ) залишиться особливою точкою після гладкого перетворення; періодична орбіта є петлею у фазовому просторі, і гладкі деформації фазового простору не зможуть змінити її як петлю. Саме в околі особливих точок і періодичних орбіт можна добре зрозуміти структуру фазового простору динамічної системи. У якісному дослідженні динамічних систем підхід полягає в тому, щоб показати, що існує заміна координат (зазвичай невизначених, але обчислюваних), що робить динамічну систему максимально простою.
Випрямлення[ред. | ред. код]
Потік на більшості невеликих підмножинах фазового простору можна зробити дуже простим. Якщо y — точка, де вектор-функція , то заміна координат відбувається для області навколо y, де векторне поле стає серією паралельних векторів однакової довжини. Це відомо як теорема випрямлення.
Теорема випрямлення говорить, що коло особливих точок динаміка точки на невеликій множині є прямою лінією. Цю множину іноді можна збільшити, з'єднавши кілька таких множин разом, і коли це спрацює, то у всьому фазовому просторі M динамічна система є інтегровною. У більшості випадків ця множина не може бути поширеною на весь фазовий простір. У вектор-фунції можуть бути особливі точки (де ); або ці множини можуть ставати все менше і менше в міру наближення до певної точки. Більш тонка причина — це глобальне обмеження, коли траєкторія починається з невеликої множини, а після відвідування ряду інших невеликих множин повертається до вихідної. Якщо наступного разу орбіта обійде фазовий простір по-іншому, то випрямити векторне поле у всій серії множин неможливо.
Околи періодичних орбіт[ред. | ред. код]
Загалом, в околах періодичної орбіти теорема випрямлення не може бути використана. Пуанкаре розробив підхід, який перетворює аналіз поблизу періодичної орбіти в аналіз відображення. Виберемо точку з орбіти γ і розглянемо точки фазового простору в її околі, перпендикулярні до . Ці точки утворюють перетин Пуанкаре орбіти. Тепер потік визначає відображення Пуанкаре для точок, які починаються в S і повертаються до S. Не всі ці точки повертаються за однакову кількість часу, але цей час буде близьким до часу, який потрібен для .
Перетин періодичної орбіти з перетином Пуанкаре є нерухомою точкою відображення Пуанкаре F. Через переміщення можна вважати, що точка знаходиться в . Ряд Тейлора відображення , тому можна очікувати, що зміна координат h лише спростить F до його лінійної частини
Це рівняння відоме як рівняння спряження. Знаходження умов для виконання цього рівняння було одним із головних завдань дослідження динамічних систем. Пуанкаре вперше підійшов до нього, вважаючи, що всі функції є аналітичними, і в процесі виявив нерезонансну умову. Якщо є власними значеннями , вони будуть резонансними, якщо одне власне значення є цілочисельною лінійною комбінацією двох або більше інших. Оскільки доданки вигляду (множини інших власних значень) зустрічаються в знаменнику доданків для функції h, то нерезонансна умова також відома як проблема малого дільника.
Спряження[ред. | ред. код]
Існування розв'язку рівняння спряження залежить від власних значень J та ступеню гладкості, необхідного від h. Оскільки J не потребує особливих симетрій, її власні значення, здебільшого, будуть комплексними числами. Коли власні значення J не знаходяться в одиничному колі, то динаміка поблизу нерухомої точки F називається гіперболічною, а коли власні значення знаходяться на одиничному колі, то динаміка називається еліптичною.
У гіперболічному випадку теорема Гробмана — Гартмана дає умови існування неперервної функції, яка відображає окіл нерухомої точки відображення на лінійне відображення . Гіперболічний випадок також структурно стійкий. Збурення у вектор-функції призведуть лише до незначних змін у відображенні Пуанкаре, і ці невеликі зміни відображатимуться в невеликих змінах положення власних значень J на комплексній площині, що означає, що відображення все ще є гіперболічним.
Теорема Колмогорова — Арнольда — Мозера (КАМ) описує поведінку поблизу еліптичної нерухомої точки.
Теорія біфуркацій[ред. | ред. код]
Коли відображення еволюції (або вектор-функція, з якого вона походить) залежить від параметра , то структура фазового простору також залежатиме від цього параметра. Збурення можуть не викликати якісних змін у фазовому просторі, поки не буде досягнуто деякого значення . У цей момент фазовий простір якісно змінюється, і кажуть, що динамічна система пройшла через біфуркацію.
Теорія біфуркацій розглядає структуру у фазовому просторі (переважно, нерухому точку, періодичну орбіту або інваріантний тор) і вивчає її поведінку як функцію параметра . У точці біфуркації структура може змінити свою стабільність, розділитися на нові структури або злитися з іншими структурами. Використовуючи апроксимацію відображення рядом Тейлора та розуміючи відмінності, які можуть бути усунені заміною координат, можна класифікувати біфуркації динамічних систем.
Біфуркації гіперболічної нерухомої точки сімейства систем можна охарактеризувати власними числами першої похідної системи , обчисленої в точці біфуркації. Для відображення біфуркація відбудеться, коли на одиничному колі є власні числа . Для потоку це відбудеться, коли на уявній осі є власні числа.
Деякі біфуркації можуть призвести до дуже складних структур у фазовому просторі. Наприклад, сценарій Руелля — Такенса описує, як періодична орбіта розгалужується на тор, а тор — на дивний атрактор. В іншому прикладі подвоєння періоду Фейгенбаума[en] описує, як стабільна періодична орбіта проходить серію біфуркацій подвоєнь періоду.
Ергодичні системи[ред. | ред. код]
У багатьох динамічних системах можна обрати систему координат так, щоб об'єм (насправді ν-вимірний об'єм) у фазовому просторі був інваріантним. Це відбувається для механічних систем, що випливають із законів Ньютона, якщо координатами є положення та імпульс, а об'єм вимірюється в одиницях (положення) × (імпульс). Потік перетворює точки підмножини A в точки , а інваріантність фазового простору означає, що
- .
У Гамільтоновій механіці за даною координатою можна вивести відповідний (узагальнений) імпульс таким чином, щоб пов'язаний об'єм зберігався потоком. Об'єм обчислюється через міру Ліувіля.
У Гамільтоновій системі не всі можливі конфігурації положення та імпульсу можуть бути досягнуті з початкової умови. Через збереження енергії доступні лише стани з такою ж енергією, що й у початкової умови. Стани з однаковою енергією утворюють енергетичну оболонку Ω, підмноговид фазового простору. Об'єм енергетичної оболонки, розрахований через міру Ліувіля, зберігається в процесі еволюції.
Для систем, де об'єм зберігається потоком, Пуанкаре відкрив теорему про рекурентність[en]: припустімо, що фазовий простір має скінченний об'єм Ліувіля, і нехай F — відображення, що зберігає об'єм фазового простору, а A — підмножина фазового простору. Тоді майже кожна точка A повертається в A нескінченно часто. Теорема Пуанкаре про рекурентність була використана Цермело, щоб заперечити проти висновку Больцмана щодо збільшення ентропії в динамічній системі атомів, що стикаються.
Одним із питань, порушених роботою Больцмана, було можливість рівності між середнім за часом та середнім за об'ємом, що він назвав ергодичною гіпотезою. Гіпотеза стверджує, що тривалість часу, за який типова траєкторія проводить в області A, дорівнює vol(A)/vol(Ω).
Виявилося, що ергодична гіпотеза не важлива для розвитку статистичної механіки, і для охоплення відповідних аспектів фізичних систем було введено ряд інших подібних властивостей. Бернард Купман[en] підійшов до вивчення ергодичних систем, використовуючи функціональний аналіз. Спостережуване a — це функція, яка до кожної точки фазового простору повертає число (наприклад, миттєвий тиск або середню висоту). Значення спостережуваного можна обчислити в інший час за допомогою функції еволюції . Для цього вводять оператор Перона — Фробеніуса[en] :
- .
Вивчаючи спектральні властивості лінійного оператора U, стає можливим класифікувати ергодичні властивості . Використовуючи підхід Купмана для розгляду дії потоку на спостережуваній функції, скінченновимірну нелінійну задачу з відображають у нескінченновимірну лінійну задачу з .
Міра Ліувіля, обмежена енергетичною поверхнею Ω, є основою для середніх, обчислених у статистичній механіці рівноваги. Середнє за часом уздовж траєкторії рівне середньому за об'ємом, обчисленому за допомогою коефіцієнта Больцмана . Цю ідею узагальнили Синай, Рюелл та Бовен (СРБ) на більший клас динамічних систем, що охоплює дисипативні системи. СРБ міри[en] замінюють коефіцієнт Больцмана та визначаються на атракторах хаотичних систем.
Нелінійні динамічні системи та хаос[ред. | ред. код]
Прості нелінійні динамічні системи і навіть кусково-лінійні системи можуть демонструвати абсолютно непередбачувану поведінку, яка може здатися випадковою, попри те, що вони в своїй основі детерміновані. Таку, здавалося б, непередбачувану поведінку називають хаосом. Гіперболічні системи — це точно визначені динамічні системи, які виявляють такі властивості, що приписуються хаотичним системам. У гіперболічних системах дотичний простір, перпендикулярний до траєкторії, можна добре розділити на дві частини: одну з точками, що сходяться до орбіти («стабільний многовид»), та іншу з точок, що розходяться від орбіти («нестабільний многовид»).
Ця галузь математики вивчає довгострокову якісну поведінку динамічних систем. Тут наголос робиться не на пошуку точних розв'язків рівнянь, що визначають динамічну систему (що часто безнадійно), а на тому, щоб відповісти на запитання на зразок «Чи прийде система до стаціонарного стану, і якщо так, то чи можливі атрактори?» або «Чи залежить довготривала поведінка системи від її початкового стану?».
Зауважимо, що питання не в хаотичній поведінці складних систем. Метеорологія, як відомо, багато років включає складну, навіть, хаотичну поведінку. Теорія хаосу була настільки дивною, бо хаос можна було знайти в майже тривіальних системах. Логістичне відображення є лише поліномом другого степеню, а підкова Смейла — кусково-лінійна.
Розв'язки скінченної тривалості[ред. | ред. код]
Для нелінійних автономних ЗДР за деяких умов можна знаходити розв'язки кінцевої тривалості,[10] тобто за своєю власною динамікою система досягне нульового значення в кінцевий момент і залишиться там на нулі назавжди. Ці розв'язки скінченної тривалості не можуть бути аналітичними функціями на всій дійсній прямій, і оскільки вони будуть неліпшицевими функціями в момент їх закінчення, в них не буде однозначності розв'язків диференціальних рівнянь Ліпшица.
Наприклад, розглянемо рівняння:
Воно допускає розв'язок скінченної тривалості:
Див. також[ред. | ред. код]
- Коливання
- Системна динаміка
- Теорія систем
- Нелінійна система
- Синергія
- Метод ізоспектральної деформації
- Дискретна система
- Центральний многовид
Література[ред. | ред. код]
- Українською
- Гащук, П. М. Лінійні динамічні системи і звичайні диференціальні рівняння. — Львів : Українські технології, 2002. — 607 с. — ISBN 9666660245.
- Синтез лінійних оптимальних динамічних систем: навч. посіб. / [О. Ю. Лозинський, А. О. Лозинський, Я. Ю. Марущак та ін.]. — Львів: Львівська політехніка, 2016. — 392 с. — ISBN 617-607-945-3.
- Трохимчук, П. П. Нелінійні динамічні системи. — Луцьк : Вежа-Друк, 2015. — 275 с. — ISBN 9786177272259. (укр.)
- Іншими мовами
- Steven H. Strogatz. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. — 2 (Studies in Nonlinearity). — Westview Press, 2014. — 528 с. — ISBN 978-0813349107. (англ.)
- D. K. Arrowsmith, C. M. Place. An Introduction to Dynamical Systems. — 1. — Cambridge University Press, 1990. — 432 с. — ISBN 978-0521316507. (англ.)
- Richard Holmgren. A First Course in Discrete Dynamical Systems. — 2 (Universitext). — Springer, 2013. — 233 с. — ISBN 978-0387947808. (англ.)
- Robert L. Devaney. An Introduction to Chaotic Dynamical Systems. — 2 (Studies in Nonlinearity). — Westview Press, 2003. — 350 с. — ISBN 978-0813340852.
- Brin M., Stuck G. Introduction to Dynamical Systems. — Cambridge University Press, 2002. — 240 с. — ISBN 9780511755316.
- Irwin M.C. Smooth dynamical systems. — Singapore – New Jersey – London – Hong Kong: World Scientific, 2001. — 260 с. — ISBN 978-9810245993.
Посилання[ред. | ред. код]
- Weisstein, Eric W. Dynamical Systems(англ.) на сайті Wolfram MathWorld.
- Анищенко В.С. (2008). Знакомство с нелинейной динамикой (лекции Соросовского профессора) (рос.) (вид. 3). Издательство УРСС, Москва.
Примітки[ред. | ред. код]
- ↑ Melby, P. та ін. (2005). Dynamics of Self-Adjusting Systems With Noise. Chaos: An Interdisciplinary Journal of Nonlinear Science. 15 (3): 033902. Bibcode:2005Chaos..15c3902M. doi:10.1063/1.1953147. PMID 16252993.
- ↑ Gintautas, V. та ін. (2008). Resonant forcing of select degrees of freedom of multidimensional chaotic map dynamics. J. Stat. Phys. 130 (3): 617. arXiv:0705.0311. Bibcode:2008JSP...130..617G. doi:10.1007/s10955-007-9444-4. S2CID 8677631.
- ↑ Jackson, T.; Radunskaya, A. (2015). Applications of Dynamical Systems in Biology and Medicine. Springer.
- ↑ Kreyszig, Erwin (2011). Advanced Engineering Mathematics. Hoboken: Wiley. ISBN 978-0-470-64613-7.
- ↑ Gandolfo, Giancarlo (2009) [1971]. Economic Dynamics: Methods and Models (вид. Fourth). Berlin: Springer. ISBN 978-3-642-13503-3.
- ↑ Holmes, Philip. «Poincaré, celestial mechanics, dynamical-systems theory and „chaos“.» Physics Reports 193.3 (1990): 137—163.
- ↑ Rega, Giuseppe (2019). Tribute to Ali H. Nayfeh (1933-2017). IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems. Springer. с. 1—2. ISBN 9783030236922. Архів оригіналу за 5 травня 2020. Процитовано 14 червня 2022.
- ↑ Ali Hasan Nayfeh. Franklin Institute Awards. The Franklin Institute. 4 лютого 2014. Архів оригіналу за 17 квітня 2020. Процитовано 25 серпня 2019.
- ↑ Galor, Oded (2010). Discrete Dynamical Systems. Springer.
- ↑ Vardia T. Haimo (1985). Finite Time Differential Equations. 1985 24th IEEE Conference on Decision and Control. с. 1729—1733. doi:10.1109/CDC.1985.268832. S2CID 45426376. Архів оригіналу за 11 березня 2022. Процитовано 14 червня 2022.
| ||||||||||||||||
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Ця стаття містить перелік посилань, але походження тверджень у ній залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (червень 2016) |
В іншому мовному розділі є повніша стаття Dynamical system(англ.). Ви можете допомогти, розширивши поточну статтю за допомогою перекладу з англійської.
|






























































































