Штучна нейронна мережа

Шту́чні нейро́нні мере́жі (ШНМ, англ. artificial neural network), які зазвичай просто називають нейронними мережами (НМ, англ. neural networks, NN) або нейромережами (англ. neural nets),[1] це обчислювальні системи, натхнені біологічними нейронними мережами, які складають мозок тварин.[2]
ШНМ ґрунтується на сукупності з'єднаних вузлів (англ. units, nodes), які називають штучними нейронами, які приблизно моделюють нейрони біологічного мозку. Кожне з'єднання, як і синапси в біологічному мозку, може передавати сигнал до інших нейронів. Штучний нейрон отримує сигнали, потім обробляє їх і може сигналізувати нейронам, з якими його з'єднано. «Сигнал» у з'єднанні це дійсне число, а вихід кожного нейрона обчислюється деякою нелінійною функцією суми його входів. З'єднання називають ребрами (англ. edges). Нейрони та ребра зазвичай мають вагу[en] (англ. weight), яка підлаштовується в процесі навчання. Вага збільшує або зменшує силу сигналу на з'єднанні. Нейрони можуть мати такий поріг, що сигнал надсилається лише тоді, коли сукупний сигнал перевищує цей поріг.
Як правило, нейрони зібрано в шари (англ. layers). Різні шари можуть виконувати різні перетворення даних свого входу. Сигнали проходять від першого шару (шару входу) до останнього (шару виходу), можливо, після проходження шарами декілька разів.
Нейронні мережі навчаються (або, їх тренують) шляхом обробки прикладів, кожен з яких містить відомий «вхід» та «результат», утворюючи ймовірнісно зважені асоціації між ними, які зберігаються в структурі даних самої мережі. Тренування нейронної мережі заданим прикладом зазвичай здійснюють шляхом визначення різниці між обробленим виходом мережі (часто, передбаченням) і цільовим виходом. Ця різниця є похибкою. Потім мережа підлаштовує свої зважені асоціації відповідно до правила навчання і з використанням цього значення похибки. Послідовні підлаштовування призведуть до виробляння нейронною мережею результатів, усе більше схожих на цільові. Після достатньої кількості цих підлаштовувань, тренування можливо припинити на основі певного критерію. Це форма керованого навчання.
Такі системи «навчаються» виконувати завдання, розглядаючи приклади, як правило, без програмування правил для конкретних завдань. Наприклад, у розпізнаванні зображень вони можуть навчитися встановлювати зображення, на яких зображені коти, аналізуючи приклади зображень, мічені[en] вручну як «кіт» та «не кіт», і використовуючи результати для ідентифікування котів на інших зображеннях. Вони роблять це без будь-якого апріорного знання про котів, наприклад, що вони мають хутро, хвости, вуса та котоподібні писки. Натомість, вони автоматично породжують ідентифікаційні характеристики з прикладів, які оброблюють.
Найпростіший тип нейронної мережі прямого поширення (НМПП, англ. feedforward neural network, FNN) це лінійна мережа, яка складається з єдиного шару вузлів виходу; входи подаються безпосередньо на виходи через низку ваг. В кожному вузлі обчислюється сума добутків ваг та даних входів. Середньоквадратичні похибки між цими обчисленими виходами та заданими цільовими значеннями мінімізують шляхом підлаштовування ваг. Цей метод відомий понад два століття як метод найменших квадратів або лінійна регресія. Лежандр (1805) та Гаусс (1795) використовували його як засіб для знаходження доброго грубого лінійного допасування до набору точок для передбачування руху планет.[3][4][5][6][7]
Вільгельм Ленц[en] та Ернст Ізінг[en] створили та проаналізували модель Ізінга (1925),[8] яка, по суті, є штучною рекурентною нейронною мережею (РНМ, англ. recurrent neural network, RNN) без навчання, що складається з нейроноподібних порогових елементів.[6] 1972 року Сун'їті Амарі[en] зробив цю архітектуру адаптивною.[9][6] Його навчання РНМ популяризував Джон Гопфілд 1982 року.[10]
Воррен Маккалох та Волтер Піттс[en][11] (1943) також розглядали ненавчану обчислювальну модель для нейронних мереж.[12] Наприкінці 1940-х років Д. О. Гебб[13] створив гіпотезу навчання, засновану на механізмі нейропластичності, що стала відомою як геббове навчання (англ. Hebbian learning). Фарлі та Веслі А. Кларк[en][14] (1954) вперше використали обчислювальні машини, звані тоді «калькуляторами», для моделювання геббової мережі. 1958 року психолог Френк Розенблат винайшов перцептрон (англ. perceptron), першу втілену штучну нейронну мережу,[15][16][17][18] фінансовану Управлінням військово-морських досліджень[en] США.[19]
Дехто каже, що дослідження зазнали застою після того, як Мінскі та Пейперт (1969)[20] виявили, що базові перцептрони не здатні обробляти схему виключного «або», і що комп'ютерам бракує достатньої потужності для обробки придатних нейронних мереж. Проте на момент виходу цієї книги вже були відомі методи тренування багатошарових перцептронів (БШП, англ. multilayer perceptron, MLP).
Перший БШП глибокого навчання опублікували Олексій Григорович Івахненко та Валентин Лапа 1965 року під назвою метод групового урахування аргументів (англ. Group Method of Data Handling).[21][22][23] Перший БШП глибокого навчання, навчений стохастичним градієнтним спуском,[24] опублікував 1967 року Сун'їті Амарі[en].[25] У комп'ютерних експериментах, проведених учнем Амарі Сайто, п'ятишаровий БШП із двома змінюваними шарами навчився корисних внутрішніх подань для класифікування нелінійно роздільних класів образів.[6]
Самоорганізаційні карти (англ. self-organizing maps, SOM) описав Теуво Кохонен 1982 року.[26][27] Самоорганізаційні карти — це нейрофізіологічно натхнені[28] нейронні мережі, які навчаються низьковимірного подання високовимірних даних, зберігаючи при цьому топологічну структуру цих даних. Вони тренуються за допомогою конкурентного навчання.[26]
Архітектуру згорткової нейронної мережі (ЗНМ, англ. convolutional neural network, CNN) зі згортковими шарами та шарами пониження дискретизації запропонував Куніхіко Фукусіма[en] 1980 року.[29] Він назвав її неокогнітроном (англ. neocognitron). 1969 року він також запропонував передавальну функцію ReLU (англ. rectified linear unit, випрямлений лінійний вузол).[30] Цей випрямляч став найпопулярнішою передавальною функцією для ЗНМ та глибоких нейронних мереж загалом.[31] ЗНМ стали важливим інструментом комп'ютерного бачення.
Алгоритм зворотного поширення (англ. backpropagation) це ефективне застосування ланцюгового правила Лейбніца (1673)[32] до мереж диференційовних вузлів. Він також відомий як зворотний режим автоматичного диференціювання або зворотне накопичення[en], завдяки Сеппо Ліннаінмаа[en] (1970).[33][34][35][36][6] Термін «похибки зворотного поширення» (англ. "back-propagating errors") запровадив 1962 року Френк Розенблат,[37][6] але він не мав втілення цієї процедури, хоча Генрі Келлі[en][38] та Брайсон[en][39] мали безперервні попередники зворотного поширення на основі динамічного програмування.[21][40][41][42] вже в 1960—61 роках у контексті теорії керування.[6] 1973 року Дрейфус використав зворотне поширення для пристосовування параметрів контролерів пропорційно градієнтам похибок.[43] 1982 року Пол Вербос[en] застосував зворотне поширення до БШП у спосіб, який став стандартним.[44][40] 1986 року Румельхарт[en], Гінтон та Вільямс[en] показали, що зворотне поширення навчається цікавих внутрішніх подань слів як векторів ознак, коли тренується передбачувати наступне слово в послідовності.[45]
Нейронна мережа з часовою затримкою (англ. time delay neural network, TDNN) Алекса Вайбеля[en] (1987) поєднала згортки, спільні ваги та зворотне поширення.[46][47] 1988 року Вей Чжан зі співавт. застосовували зворотне поширення до ЗНМ (спрощеного неокогнітрона зі згортковими взаємозв'язками між шарами ознак зображення та останнім повнозв'язним шаром) для абеткового розпізнавання.[48][49] 1989 року Ян Лекун зі співавт. навчили ЗНМ розпізнавати рукописні поштові індекси на пошті.[50] 1992 року Джуан Венг зі співавт. запропонували максимізувальне агрегування (англ. max-pooling) для ЗНМ, щоби допомогти з інваріантністю щодо найменшого зсуву та толерантністю до деформування для сприяння розпізнаванню тривимірних об'єктів[en].[51][52][53] LeNet-5 (1998), 7-рівневу ЗНМ від Яна Лекуна зі співавт.,[54] яка класифікує цифри, було застосовано кількома банками для розпізнавання рукописних чисел на чеках, оцифрованих у зображення 32×32 пікселів.
Починаючи з 1988 року[55][56] використання нейронних мереж перетворило галузь передбачування структур білків, зокрема, коли перші каскадні мережі тренувалися на профілях (матрицях), створених численними вирівнюваннями послідовностей.[57]
У 1980-х роках зворотне поширення не працювало добре для глибоких НМПП та РНМ. Щоби подолати цю проблему, Юрген Шмідхубер (1992) запропонував ієрархію РНМ, попередньо тренованих по одному рівню самокерованим навчанням.[58][59] Вона використовує передбачувальне кодування[en] для навчання внутрішніх подань у кількох самоорганізованих масштабах часу. Це може істотно полегшувати подальше глибоке навчання. Цю ієрархію РНМ можливо згорнути (англ. collapse) в єдину РНМ шляхом дистилювання[en] фрагментувальної (англ. chunker) мережі вищого рівня в автоматизувальну (англ. automatizer) мережу нижчого рівня.[58][6] 1993 року фрагментувальник розв'язав завдання глибокого навчання, глибина якого перевищувала 1000.[60]
1992 року Юрген Шмідхубер також опублікував альтернативу РНМ (англ. alternative to RNNs),[61] яку зараз називають лінійним трансформером (англ. linear Transformer) або трансформером з лінеаризованою самоувагою[62][63][6] (за винятком оператора нормування). Він навчається внутрішніх центрів уваги (англ. internal spotlights of attention):[64] повільна нейронна мережа прямого поширення вчиться за допомогою градієнтного спуску керувати швидкими вагами іншої нейронної мережі через тензорні добутки самопороджуваних шаблонів збудження FROM і TO (званих тепер ключем, англ. key, та значенням, англ. value, самоуваги).[62] Це відображення уваги (англ. attention mapping) швидких ваг застосовують до шаблону запиту.
Сучасний трансформер (англ. Transformer) запропонували Ашиш Васвані зі співавт. у своїй праці 2017 року «Увага — це все, що вам треба».[65] Він поєднує це з оператором softmax та проєкційною матрицею.[6] Трансформери все частіше обирають за модель для обробки природної мови.[66] Багато сучасних великих мовних моделей, таких як ChatGPT, GPT-4 та BERT, використовують саме його. Трансформери також все частіше використовують у комп'ютернім баченні.[67]
1991 року Юрген Шмідхубер також опублікував змагальні нейронні мережі (англ. adversarial neural networks), які змагаються між собою у формі антагоністичної гри, де виграш однієї мережі є програшем іншої.[68][69][70] Перша мережа є породжувальною моделлю, яка моделює розподіл імовірності над образами на виході. Друга мережа навчається градієнтним спуском передбачувати реакцію середовища на ці образи. Це було названо «штучною цікавістю» (англ. "artificial curiosity").
2014 року Ян Ґудфелоу зі співавт. використали цей принцип у породжувальній змагальній мережі (англ. generative adversarial network, GAN).[71] Тут реакція навколишнього середовища дорівнює 1 або 0 залежно від того, чи належить вихід першої мережі до заданого набору. Це можливо використовувати для створення реалістичних дипфейків.[72] Відмінної якості зображення досягла StyleGAN[en] Nvidia (2018)[73] на основі прогресивної породжувальної змагальної мережі (англ. Progressive GAN) Теро Карраса, Тімо Айли, Самулі Лайне та Яакко Лехтінена.[74] Тут породжувач вирощується від малого до великого пірамідним чином.
Дипломну працю Зеппа Хохрайтера[en] (1991)[75] його керівник Юрген Шмідхубер назвав «одним із найважливіших документів в історії машинного навчання».[6] Хохрайтер визначив і проаналізував проблему зникання градієнту[75][76] й запропонував для її розв'язання рекурентні залишкові з'єднання. Це призвело до появи методу глибокого навчання, званого довгою короткочасною пам'яттю (ДКЧП, англ. long short-term memory, LSTM), опублікованого в Neural Computation (1997).[77] Рекурентні нейронні мережі ДКЧП можуть навчатися задач «дуже глибокого навчання» (англ. "very deep learning")[78] з довгими шляхами розподілу внеску, які вимагають спогадів про події, що відбулися за тисячі дискретних часових кроків до цього. «Стандартну ДКЧП» (англ. "vanilla LSTM") із забувальним вентилем запропонували 1999 року Фелікс Ґерс[en], Шмідхубер та Фред Каммінс.[79] ДКЧП стала найцитованішою нейронною мережею XX століття.[6] 2015 року Рупеш Кумар Шрівастава, Клаус Ґрефф і Шмідхубер використали принцип ДКЧП для створення магістралевої мережі (англ. Highway network), нейронної мережі прямого поширення з сотнями шарів, набагато глибшої за попередні.[80][81] 7 місяців потому, Каймін Хе, Сян'ю Чжан; Шаоцін Рен та Цзянь Сунь виграли змагання ImageNet[en] 2015 року з відкритовентильним або безвентильним варіантом магістралевої мережі, названим залишковою нейронною мережею (англ. Residual neural network).[82] Вона стала найцитованішою нейронною мережею XXI століття.[6]
Розвиток метал-оксид-напівпровідникових (МОН) схем надвисокого рівня інтеграції (НВІС) у формі технології комплементарних МОН (КМОН) дозволив збільшити кількість[en] МОН-транзисторів у цифровій електроніці. Це забезпечило більшу потужність обробки для розробки практичних штучних нейронних мереж у 1980-х роках.[83]
До ранніх успіхів нейронних мереж належали прогнозування фондового ринку, а 1995 року (переважно) безпілотний автомобіль.[a][84]
Джефрі Гінтон зі співавт. (2006) запропонували навчання високорівневих подань з використанням послідовних шарів двійкових або дійснозначних латентних змінних з обмеженою машиною Больцмана[85] для моделювання кожного шару. 2012 року Ин та Дін створили мережу, яка навчилася розпізнавати поняття вищого рівня, такі як коти, лише переглядаючи немічені зображення.[86] Попереднє некероване тренування та збільшення обчислювальної потужності ГП та розподілених обчислень дозволили використовувати більші мережі, зокрема в задачах розпізнавання зображень і бачення, які стали відомі як «глибоке навчання».[87]
Чирешан із колегами (2010)[88] показали, що, незважаючи на проблему зникання градієнта, ГП роблять зворотне поширення придатним для багатошарових нейронних мереж прямого поширення.[89] У період між 2009 та 2012 роками ШНМ почали вигравати нагороди в конкурсах із розпізнавання зображень, наближаючись до людського рівня виконання різних завдань, спочатку в розпізнаванні образів та розпізнаванні рукописного тексту.[90][91] Наприклад, двоспрямована та багатовимірна довга короткочасна пам'ять (ДКЧП)[92][93] Ґрейвса[en] зі співавт. виграла три змагання з розпізнавання зв'язаного рукописного тексту 2009 року без будь-яких попередніх знань про три мови, яких потрібно було навчитися.[92][93]
Чирешан із колегами створили перші розпізнавачі образів, які досягли людської/надлюдської продуктивності[94] на таких перевірках як розпізнавання дорожніх знаків (IJCNN 2012).
| Цей розділ може бути плутаним чи неясним[en] для читачів. (січень 2018) |

ШНМ почалися як спроба використати архітектуру людського мозку для виконання завдань, у яких звичайні алгоритми мали невеликий успіх. Незабаром вони переорієнтувалися на покращення емпіричних результатів, відмовившись від спроб залишатися вірними своїм біологічним попередникам. ШНМ мають здатність навчатися нелінійностей та складних зв'язків та моделювати їх. Це досягається тим, що нейрони з'єднуються за різними схемами, що дозволяє виходам одних нейронів стати входом інших. Ця мережа утворює орієнтований зважений граф.[95]
Штучна нейронна мережа складається з імітацій нейронів. Кожен нейрон з'єднано з іншими вузлами (англ. nodes) ланками (англ. links), як біологічне з'єднання аксон—синапс—дендрит. Усі вузли, з'єднані ланками, отримують деякі дані й використовують їх для виконання певних операцій і завдань з даними. Кожна ланка має вагу (англ. weight), що визначає силу впливу одного вузла на інший,[96] дозволяючи вагам обирати сигнал між нейронами.
ШНМ складаються зі штучних нейронів, які концептуально походять від біологічних. Кожен штучний нейрон має входи та видає єдиний вихід, який можливо надсилати багатьом іншим нейронам.[97] Входи (англ. inputs) можуть бути значеннями ознак зразка зовнішніх даних, таких як зображення чи документи, або вони можуть бути виходами інших нейронів. Виходи кінцевих нейронів виходу (англ. output neurons) нейронної мережі завершують завдання, наприклад, розпізнавання об'єкта на зображенні.
Щоби знайти вихід нейрона, ми беремо зважену суму всіх входів, зважених за вагами з'єднань (англ. connection weights) від входів до нейрона. Ми додаємо до цієї суми зміщення (англ. bias).[98] Цю зважену суму іноді називають збудженням (англ. activation). Цю зважену суму потім пропускають крізь (зазвичай нелінійну) передавальну функцію (англ. activation function) для отримання виходу. Первинними входами є зовнішні дані, наприклад зображення та документи. Кінцеві виходи завершують завдання, наприклад, розпізнавання об'єкта на зображенні.[99]
Нейрони зазвичай впорядковано в кілька шарів (англ. layers), особливо в глибокому навчанні. Нейрони одного шару з'єднуються лише з нейронами безпосередньо попереднього й наступного шарів. Шар, який отримує зовнішні дані, це шар входу (англ. input layer). Шар, який видає кінцевий результат, це шар виходу (англ. output layer). Між ними є нуль або більше прихованих шарів (англ. hidden layers). Використовують також одношарові (англ. single layer) та безшарові (англ. unlayered) мережі. Між двома шарами можливі кілька схем з'єднання. Вони можуть бути «повноз'єднаними» (англ. 'fully connected'), коли кожен нейрон одного шару з'єднується з кожним нейроном наступного шару. Вони можуть бути агрегувальними (англ. pooling), коли група нейронів одного шару з'єднується з одним нейроном наступного шару, знижуючи таким чином кількість нейронів у цьому шарі.[100] Нейрони лише з такими зв'язками утворюють орієнтований ациклічний граф і відомі як мережі прямого поширення (англ. feedforward networks).[101] Крім того, мережі, які дозволяють з'єднання до нейронів у тому же або попередніх шарах, відомі як рекурентні мережі (англ. recurrent networks).[102]
Гіперпараметр (англ. hyperparameter) — це сталий параметр, чиє значення встановлюють перед початком процесу навчання. Значення же параметрів (англ. parameters) виводять шляхом навчання. До прикладів гіперпараметрів належать темп навчання (англ. learning rate), кількість прихованих шарів і розмір пакета.[103] Значення деяких гіперпараметрів можуть залежати від значень інших гіперпараметрів. Наприклад, розмір деяких шарів може залежати від загальної кількості шарів.
| Цей розділ містить перелік посилань, але походження тверджень у ньому залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (липень 2023) |
Навчання (англ. learning) — це пристосовування мережі для кращого виконання завдання шляхом розгляду вибіркових спостережень. Навчання включає підлаштовування ваг (і, можливо, порогів) мережі для підвищення точності результатів. Це здійснюється шляхом мінімізування спостережуваних похибок. Навчання завершено, якщо розгляд додаткових спостережень не знижує рівня похибки. Навіть після навчання рівень похибки зазвичай не досягає 0. Якщо навіть після навчання рівень похибки занадто високий, зазвичай потрібно змінити будову мережі. Практично це здійснюють шляхом визначення функції витрат (англ. cost function), яку періодично оцінюють протягом навчання. Поки її результат знижується, навчання триває. Витрати часто визначають як статистику, значення якої можливо лише наближувати. Виходи насправді є числами, тож коли похибка низька, різниця між результатом (майже напевно кіт) і правильною відповіддю (кіт) невелика. Навчання намагається знизити загальну відмінність над спостереженнями. Більшість моделей навчання можливо розглядати як пряме застосування теорії оптимізації та статистичного оцінювання.[95][104]
Темп навчання (англ. learning rate) визначає розмір коригувальних кроків, які здійснює модель для підлаштовування під похибку в кожному спостереженні.[105] Високий темп навчання скорочує тривалість тренування, але з меншою кінцевою точністю, тоді як нижчий темп навчання займає більше часу, але з потенціалом до більшої точності. Такі оптимізації, як Quickprop[en] (укр. «швидпошир»), переважно спрямовані на прискорення мінімізування похибки, тоді як інші вдосконалення переважно намагаються підвищити надійність. Щоби запобігти циклічним коливанням усередині мережі, таким як чергування ваг з'єднань, і покращити швидкість збігання, удосконалення використовують адаптивний темп навчання, який підвищується або знижується належним чином.[106] Концепція імпульсу (англ. momentum) дозволяє зважувати баланс між градієнтом і попередньою зміною так, щоби підлаштовування ваги певною мірою залежало від попередньої зміни. Імпульс, близький до 0, додає ваги градієнтові, тоді як значення, близьке до 1, додає ваги крайній зміні.
Хоча й можливо визначати функцію витрат ad hoc, вибір часто визначається бажаними властивостями цієї функції (такими як опуклість) або тим, що вона постає з моделі (наприклад, у ймовірнісній моделі апостеріорну ймовірність моделі можливо використовувати як обернені витрати).
Зворотне поширення (англ. backpropagation) — це метод, який використовують для підлаштовування ваг з'єднань для компенсування кожної помилки, виявленої під час навчання. Величина помилки фактично розподіляється між з'єднаннями. Технічно зворотне поширення обчислює градієнт (похідну) функції витрат, пов'язаний із заданим станом, відносно ваг. Уточнювання ваг можливо здійснювати за допомогою стохастичного градієнтного спуску (англ. stochastic gradient descent) або інших методів, таких як машини екстремального навчання,[107] «безпоширні» (англ. "no-prop") мережі,[108] тренування без вертання,[109] «безвагові» (англ. "weightless") мережі,[110][111] та не-конективістські нейронні мережі[en].[джерело?]
| Цей розділ містить перелік посилань, але походження тверджень у ньому залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (липень 2023) |
Машинне навчання зазвичай поділяють на три основні парадигми: кероване навчання,[112][113][114][115] некероване навчання[116][113][114][117][115] та навчання з підкріпленням.[118][119] Кожна відповідає певному навчальному завданню.
Кероване навчання[113][114][115] (англ. supervised learning) використовує набір пар входів і бажаних виходів. Завдання навчання полягає в тому, щоби для кожного входу видавати бажаний вихід. У цьому випадку функція витрат пов'язана з усуненням неправильного висновування.[120] Витрати, які використовують зазвичай, це середньоквадратична похибка, яка намагається мінімізувати середню квадратичну похибку виходу мережі відносно бажаного виходу. Для керованого навчання підходять завдання на розпізнавання образів (також відоме як класифікування) та регресію (також відоме як наближення функції). Кероване навчання також застосовне до послідовних даних (наприклад, для розпізнавання рукописного тексту, мовлення та жестів[en]). Його можливо розглядати як навчання з «учителем» у вигляді функції, яка забезпечує безперервний зворотний зв'язок щодо якості отриманих на даний момент рішень.
У некерованім навчанні[113][114][117][115] (англ. unsupervised learning) дані входу надаються разом із функцією витрат, деякою функцією від даних та виходу мережі. Функція витрат залежить від завдання (області моделі) та будь-яких апріорних припущень (неявних властивостей моделі, її параметрів та спостережуваних змінних). Як тривіальний приклад розгляньмо модель , де стала, а витрати . Мінімізація цих витрат дає значення , що дорівнює середньому значенню даних. Функція витрат може бути набагато складнішою. Її вигляд залежить від застосування: наприклад, у стисненні вона може бути пов'язаною із взаємною інформацією між та , тоді як у статистичному моделюванні вона може бути пов'язаною з апостеріорною ймовірністю моделі за заданих даних (зверніть увагу, що в обох цих прикладах ці величини підлягають максимізуванню, а не мінімізуванню). Завдання, які підпадають під парадигму некерованого навчання, це зазвичай задачі оцінювання; до цих застосувань належать кластерування, оцінювання статистичних розподілів, стискання та фільтрування.
У таких застосуваннях як гра у відеоігри, діяч (англ. actor) виконує низку дій (англ. actions), отримуючи загалом непередбачуваний відгук від середовища після кожної з них. Мета полягає в тому, щоби виграти гру, тобто породити найбільшу кількість позитивних (з найменшими витратами) відгуків. У навчанні з підкріпленням (англ. reinforcement learning) мета полягає в тому, щоби зважити мережу (розробити стратегію, англ. policy) для виконання дій, яка мінімізує довгострокові (очікувані сукупні) витрати. У кожен момент часу діяч виконує дію, а середовище породжує спостереження та миттєві витрати відповідно до деяких (зазвичай невідомих) правил. Зазвичай правила й довгострокові витрати можливо лише оцінювати. У будь-який момент діяч вирішує, чи дослідити нові дії, щоб розкрити свої витрати, а чи скористатися попереднім знанням для швидшого виконання.
Формально середовище моделюють як марковський процес вирішування (МПВ) зі станами та діями . Оскільки переходи станів невідомі, замість них використовують розподіли ймовірності: розподіл миттєвих витрат , розподіл спостережень та розподіл переходів , тоді як стратегію визначають як умовний розподіл дій за даних спостережень. Взяті разом, вони визначають марковський ланцюг (МЛ). Мета полягає у виявленні МЛ із найменшими витратами.
ШНМ у таких застосуваннях слугують складовою, яка забезпечує навчання.[121][122] Динамічне програмування у поєднанні з ШНМ (що дає нейродинамічне програмування)[123] було застосовано до таких задач як ті, що стосуються маршрутизуваня транспорту[en],[124] відеоігор, природокористування[125][126] та медицини,[127] через здатність ШНМ пом'якшувати втрати точності навіть при зменшенні щільності ґратки дискретування[en] для чисельного наближення розв'язків задач керування. Завдання, які підпадають під парадигму навчання з підкріпленням, це завдання керування, ігри та інші послідовні завдання ухвалювання рішень.
Самонавчання (англ. self-learning) в нейронних мережах було запропоновано 1982 року разом із нейронною мережею, здатною до самонавчання, названою поперечинним адаптивним масивом (ПАМ, англ. crossbar adaptive array, CAA).[128] Це система лише з одним входом, ситуацією s, й лише одним виходом, дією (або поведінкою) a. Вона не має ані входу зовнішніх порад, ані входу зовнішнього підкріплення з боку середовища. ПАМ обчислює поперечним чином як рішення щодо дій, так і емоції (почуття) щодо виниклих ситуацій. Ця система керується взаємодією між пізнанням та емоціями.[129] За заданої матриці пам'яті, W =||w(a, s)||, поперечинний алгоритм самонавчання на кожній ітерації виконує наступне обчислення:
У ситуації s виконати дію a; Отримати наслідкову ситуацію s'; Обчислити емоцію перебування в наслідковій ситуації v(s'); Уточнити поперечинну пам'ять w'(a,s) = w(a,s) + v(s').
Поширюване зворотно значення (вторинне підкріплення, англ. secondary reinforcement) — це емоція щодо наслідків ситуації. ПАМ існує у двох середовищах: одне — поведінкове середовище, де вона поводиться, а інше — генетичне середовище, де вона спочатку й лише один раз отримує початкові емоції щодо ситуацій, з якими можливо зіткнутися в поведінковому середовищі. Отримавши геномний вектор (видовий вектор, англ. genome vector, species vector) із генетичного середовища, ПАМ навчатиметься цілеспрямованої поведінки в поведінковому середовищі, що містить як бажані, так і небажані ситуації.[130]
Нейроеволюція (англ. neuroevolution) може створювати топології та ваги нейронної мережі за допомогою еволюційного обчислення. Завдяки сучасним вдосконаленням нейроеволюція конкурує зі складними підходами градієнтного спуску.[131] Одна з переваг нейроеволюції полягає в тому, що вона може бути менш схильною потрапляти в «глухий кут».[132]
Стохастичні нейронні мережі (англ. stochastic neural networks), що походять від моделей Шеррінгтона — Кіркпатріка[en], це один з типів штучних нейронних мереж, побудований шляхом введення випадкових варіацій у мережу, або надаванням штучним нейронам мережі стохастичних передавальних функцій, або надаванням їм стохастичних ваг. Це робить їх корисними інструментами для розв'язування задач оптимізації, оскільки випадкові флуктуації допомагають мережі уникати локальних мінімумів.[133] Стохастичні нейронні мережі, треновані за допомогою баєсового підходу, відомі як баєсові нейронні мережі (англ. Bayesian neural network).[134]
У баєсовій системі обирають розподіл над набором дозволених моделей таким чином, щоби мінімізувати витрати. Іншими алгоритмами навчання є еволюційні методи,[135] генно-експресійне програмування[en],[136] імітування відпалювання,[137] очікування-максимізація, непараметричні методи[en] та метод рою частинок.[138] Збіжна рекурсія (англ. convergent recursion) — це алгоритм навчання для нейронних мереж артикуляційних контролерів мозочкової моделі[en] (АКММ, англ. cerebellar model articulation controller, CMAC).[139][140]
| Цей розділ містить перелік посилань, але походження тверджень у ньому залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (липень 2023) |
Є два режими навчання: стохастичний (англ. stochastic) та пакетний (англ. batch). У стохастичному навчанні кожен вхід створює підлаштовування ваг. У пакетному навчанні ваги підлаштовують на основі пакету входів, накопичуючи похибки в пакеті. Стохастичне навчання вносить «шум» до процесу, використовуючи локальний градієнт, розрахований з однієї точки даних; це знижує шанс застрягання мережі в локальних мінімумах. Проте пакетне навчання зазвичай дає швидший і стабільніший спуск до локального мінімуму, оскільки кожне уточнення виконується в напрямку усередненої похибки пакета. Поширеним компромісом є використання «мініпакетів» (англ. "mini-batches"), невеликих пакетів зі зразками в кожному пакеті, обраними стохастично з усього набору даних.
ШНМ еволюціювали у широке сімейство методик, які вдосконалили рівень останніх досягнень у багатьох областях. Найпростіші типи мають один або кілька статичних складових, включно з кількістю вузлів, кількістю шарів, вагами вузлів і топологією. Динамічні типи дозволяють одному або декільком із них еволюціювати шляхом навчання. Останнє набагато складніше, але може скорочувати періоди навчання й давати кращі результати. Деякі типи дозволяють/вимагають навчання «під керуванням» оператора, тоді як інші працюють незалежно. Деякі типи працюють виключно апаратно, тоді як інші є суто програмними й працюють на комп'ютерах загального призначення.
До деяких з основних проривів належать: згорткові нейронні мережі, які виявилися особливо успішними в обробці візуальних та інших двовимірних даних;[141][142] довга короткочасна пам'ять, що дозволяє уникати проблеми зникання градієнта[143] й може обробляти сигнали, які містять суміш низько- та високочастотних складових, що допомагає в розпізнаванні мовлення з великим словниковим запасом,[144][145] синтезуванні мовлення з тексту[146][40][147] та фотореалістичних головах, що розмовляють;[148] конкурентні мережі (англ. competitive networks), такі як породжувальні змагальні мережі,[149] в яких численні мережі (різної структури) змагаються одна з одною в таких завданнях як перемога в грі, або введення опонента в оману щодо автентичності входу.[71]
Пошук нейронної архітектури (ПНА, англ. neural architecture search, NAS) використовує машинне навчання для автоматизування побудови ШНМ. Різні підходи до ПНА побудували мережі, добре порівнянні з системами, розробленими вручну. Основним алгоритмом цього пошуку є пропонувати модель-кандидатку, оцінювати її за набором даних, і використовувати результати як зворотний зв'язок для навчання мережі ПНА.[150] Серед доступних систем — АвтоМН та AutoKeras.[151]
До проблем побудови належать визначення кількості, типу та з'єднаності рівнів мережі, а також розміру кожного, та типу з'єднання (повне, агрегувальне, …).
Гіперпараметри також слід визначати як частину побудови (їх не навчаються), керуючи такими питаннями як кількість нейронів у кожному шарі, темп навчання, крок, крок фільтрів (англ. stride), глибина, рецептивне поле та доповнення (для ЗНМ) тощо.[152]
| Цей розділ не містить посилань на джерела. (липень 2023) |
Використання штучних нейронних мереж вимагає розуміння їхніх характеристик.
- Вибір моделі: Це залежить від подання даних та застосування. Надмірно складні моделі навчаються повільно.
- Алгоритм навчання: Існують численні компроміси між алгоритмами навчання. Майже кожен алгоритм працюватиме добре з правильними гіперпараметрами[153] для тренування на певному наборі даних. Проте обрання та налаштування алгоритму для навчання на небачених даних вимагає значного експериментування.
- Робастність: Якщо модель, функцію витрат та алгоритм навчання обрано належним чином, то отримана ШНМ може стати робастною.
Можливості ШНМ підпадають під наступні широкі категорії:[154]
- Наближування функцій[en],[155] або регресійний аналіз,[156] включно з передбачуванням часових рядів, наближуванням допасованості[en][157] та моделюванням.
- Класифікування, включно з розпізнаванням образів та послідовностей, виявлянням новизни[en] та послідовним ухвалюванням рішень.[158]
- Обробка даних,[159] включно з фільтруванням, кластеруванням, сліпим виокремлюванням сигналу[en][160] та стисканням.
- Робототехніка, включно зі скеровуванням маніпуляторів та протезів.
Завдяки своїй здатності відтворювати та моделювати нелінійні процеси штучні нейронні мережі знайшли застосування в багатьох дисциплінах. До сфер застосування належать ідентифікування систем[en] та керування ними (керування транспортними засобами, передбачування траєкторії,[161] керування процесами, природокористування), квантова хімія,[162] універсальна гра в ігри[en],[163] розпізнавання образів (радарні системи, встановлювання облич, класифікування сигналів,[164] тривимірна відбудова,[165] розпізнавання об'єктів тощо), аналіз даних давачів,[166] розпізнавання послідовностей (розпізнавання жестів, мовлення, рукописного та друкованого тексту[167]), медична діагностика, фінанси[168] (наприклад, передподійні[en] моделі для окремих фінансових довготривалих прогнозів та штучні фінансові ринки[en]), добування даних, унаочнювання, машинний переклад, соціальномережне фільтрування[169] та фільтрування спаму електронної пошти[en]. ШНМ використовували для діагностування кількох типів раку[170][171] та для відрізнювання високоінвазивних ліній ракових клітин від менш інвазивних з використанням лише інформації про форму клітин.[172][173]
ШНМ використовували для прискорювання аналізу надійності інфраструктури, що піддається стихійним лихам,[174][175] і для прогнозування просідання фундаментів.[176] Також може бути корисним пом'якшувати повені шляхом використання ШНМ для моделювання дощового стоку.[177] ШНМ також використовували для побудови чорноскринькових моделей в геонауках: гідрології,[178][179] моделюванні океану та прибережній інженерії[en],[180][181] та геоморфології.[182] ШНМ використовують у кібербезпеці з метою розмежовування законної діяльності від зловмисної. Наприклад, машинне навчання використовували для класифікування зловмисного програмного забезпечення під Android,[183] для визначання доменів, що належать суб'єктам загрози, і для виявляння URL-адрес, які становлять загрозу безпеці.[184] Ведуться дослідження систем ШНМ, призначених для випробування на проникнення, для виявляння бот-мереж,[185] шахрайства з кредитними картками[186] та мережних вторгнень.
ШНМ пропонували як інструмент для розв'язування частинних диференціальних рівнянь у фізиці[187][188][189] та моделювання властивостей багаточастинкових відкритих квантових систем[en].[190][191][192][193] У дослідженні мозку ШНМ вивчали короткочасну поведінку окремих нейронів,[194] динаміку нейронних ланцюгів, що виникає через взаємодію між окремими нейронами, та те, як поведінка може виникати з абстрактних нейронних модулів, які подають цілі підсистеми. Дослідження розглядали довгострокову та короткочасну пластичність нейронних систем та їхній зв'язок із навчанням і пам'яттю від окремого нейрона до системного рівня.
Як доведено теоремою Цибенка, багатошаровий перцептрон це універсальний[en] наближувач функцій. Проте це доведення не конструктивне щодо кількості необхідних нейронів, топології мережі, ваг, та параметрів навчання.
Особлива рекурентна архітектура з раціональнозначними вагами (на противагу до повноточнісних дійснозначних ваг) має потужність універсальної машини Тюрінга,[195] використовуючи скінченну кількість нейронів та стандартні лінійні з'єднання. Крім того, використання ірраціональних значень для ваг дає в результаті машину з надтюрінговою потужністю.[196][197][відсутнє в джерелі]
Властивість «ємності»[198][199] (англ. "capacity") моделі відповідає її здатності моделювати будь-яку задану функцію. Вона пов'язана з обсягом інформації, який можливо зберегти в мережі, та з поняттям складності. Серед спільноти відомі два поняття ємності: інформаційна ємність та ВЧ-розмірність. Інформаційну ємність (англ. information capacity) перцептрона ретельно обговорено в книзі сера Девіда Маккея,[200] яка підсумовує роботу Томаса Ковера.[201] Ємність мережі стандартних нейронів (не згорткових) можливо отримувати за чотирма правилами,[202] які випливають із розуміння нейрона як електричного елемента. Інформаційна ємність охоплює функції, які можливо змоделювати мережею, за довільних даних входу. Друге поняття — ВЧ-розмірність (англ. VC Dimension). ВЧ-розмірність використовує принципи теорії міри та знаходить максимальну ємність за найкращих можливих обставин. Це за даних входу певного вигляду. Як зазначено у [200], ВЧ-розмірність для довільних входів становить половину інформаційної ємності перцептрона. ВЧ-розмірність для довільних точок іноді називають ємністю пам'яті (англ. Memory Capacity).[203]
Моделі можуть не збігатися послідовно на єдиному розв'язку, по-перше, через можливість існування локальних мінімумів, залежно від функції витрат та моделі. По-друге, вживаний метод оптимізації може не гарантувати збіжності, якщо він починається далеко від будь-якого локального мінімуму. По-третє, для досить великих даних або параметрів деякі методи стають непрактичними.
Інша варта згадки проблема полягає в тому, що навчання може проходити крізь деяку сідлову точку, що може призводити до збігання в неправильному напрямку.
Поведінка збіжності певних типів архітектур ШНМ зрозуміліша, ніж інших. Коли ширина мережі наближається до нескінченності, ШНМ добре описується своїм розвиненням у ряд Тейлора першого порядку протягом навчання, і тому успадковує поведінку збіжності афінних моделей[en].[204][205] Інший приклад: коли параметри малі, спостерігається, що ШНМ часто допасовуються до цільових функцій від низьких до високих частот. Таку поведінку називають спектральним зміщенням (англ. spectral bias) або частотним принципом (англ. frequency principle) нейронних мереж.[206][207][208][209] Це явище протилежне поведінці деяких добре вивчених ітераційних числових схем, таких як метод Якобі. Було виявлено, що глибші нейронні мережі схильніші до низькочастотних функцій.[210]
| Цей розділ містить перелік посилань, але походження тверджень у ньому залишається незрозумілим через практично повну відсутність внутрішньотекстових джерел-виносок. (липень 2023) |
Застосування, метою яких є створення системи, що добре узагальнюється до невідомих зразків, стикаються з можливістю перетренування. Воно виникає в заплутаних або надмірно визначених системах, коли ємність мережі значно перевищує потребу у вільних параметрах. Існує два підходи, як впоруватися з перетренуванням. Перший полягає у використанні перехресного затверджування та подібних методів для перевірки наявності перенавчання, та обиранні гіперпараметрів для зведення похибки узагальнення до мінімуму.
Другий полягає у використанні якогось із видів регуляризації. Це поняття виникає в імовірнісній (баєсовій) системі, де регуляризацію можливо виконувати шляхом обирання більшої апріорної ймовірності над простішими моделями, але також і в теорії статистичного навчання, де метою є зводити до мінімуму дві величини: «емпіричний ризик» та «структурний ризик», що грубо відповідають похибці над тренувальним набором та передбачуваній похибці в небачених даних через перенавчання.

Нейронні мережі керованого навчання, які використовують як функцію витрат середньоквадратичну похибку (СКП), для визначення довіри до тренованої моделі можуть використовувати формальні статистичні методи. СКП на затверджувальному наборі можливо використовувати як оцінку дисперсії. Це значення потім можливо використовувати для обчислення довірчого інтервалу виходу мережі, виходячи з нормального розподілу. Здійснений таким чином аналіз довіри статистично чинний, поки розподіл імовірності виходу залишається незмінним, і не вноситься змін до мережі.
Призначення нормованої експоненційної функції, узагальнення логістичної функції, як передавальної функції шару виходу нейронної мережі (або нормованої експоненційної складової в нейронній мережі на основі складових) для категорійних цільових змінних, дає можливість інтерпретувати виходи як апостеріорні ймовірності. Це корисно для класифікування, оскільки дає міру впевненості в класифікаціях.
Нормована експоненційна функція (англ. softmax) це
Поширена критика нейронних мереж, особливо в робототехніці, полягає в тому, що для роботи в реальному світі вони вимагають забагато тренування.[211] До потенційних розв'язань належить випадкове переставляння тренувальних зразків, застосування алгоритму чисельної оптимізації, який не вимагає завеликих кроків при зміні з'єднань мережі слідом за зразком, групування зразків до так званих міні-пакетів (англ. mini-batches) та/або запровадження алгоритму рекурсивних найменших квадратів для АКММ[en].[139]
Головна претензія[джерело?] ШНМ полягає в тому, що вони втілюють нові потужні загальні принципи обробки інформації. Ці принципи погано визначені. Часто стверджують,[хто?] що вони виникають із самої мережі. Це дозволяє описувати просту статистичну асоціацію (основну функцію штучних нейронних мереж) як навчання або розпізнавання. 1997 року Олександр Дьюдні[en] зауважив, що, в результаті, штучні нейронні мережі мають «риси чогось дармового, чогось наділеного особливою аурою ледарства та виразної відсутності зацікавлення хоч би тим, наскільки добрими ці комп'ютерні системи є. Жодного втручання людської руки (та розуму), розв'язки знаходяться мов чарівною силою, і ніхто, схоже, так нічого й не навчився».[212] Однією з відповідей Дьюдні є те, що нейронні мережі розв'язують багато складних і різноманітних завдань, починаючи від автономного літального апарата[213] до виявляння шахрайства з кредитними картками, й завершуючи опануванням гри в Ґо.
Письменник у галузі технологій Роджер Бріджмен прокоментував це так:
Нейронні мережі, наприклад, знаходяться на лаві підсудних не лише через те, що їх розрекламували до небес (хіба ні?), а й через те, що ви можете створити успішну мережу, не розуміючи, як вона працює: купа чисел, які фіксують її поведінку, ймовірно, буде «непрозорою, нечитабельною таблицею... нічого не вартою як науковий ресурс».Незважаючи на свою експресивну заяву про те, що наука — це не технологія, Дьюдні, здається, ганьбить нейронні мережі як погану науку, тоді як більшість із тих, хто їх розробляє, просто намагаються бути добрими інженерами. Нечитабельна таблиця, яку може читати корисна машина, все одно буде вельми варта того, щоби її мати.[214]
Оригінальний текст (англ.)Neural networks, for instance, are in the dock not only because they have been hyped to high heaven, (what hasn't?) but also because you could create a successful net without understanding how it worked: the bunch of numbers that captures its behaviour would in all probability be "an opaque, unreadable table...valueless as a scientific resource".
In spite of his emphatic declaration that science is not technology, Dewdney seems here to pillory neural nets as bad science when most of those devising them are just trying to be good engineers. An unreadable table that a useful machine could read would still be well worth having.
Біологічний мозок використовує як неглибокі, так і глибокі схеми, як повідомляє анатомія мозку,[215] демонструючи широкий спектр інваріантності. Венг[216] стверджував, що мозок самостійно встановлює зв'язки в основному відповідно до статистики сигналів, і тому послідовний каскад не може вловити всі основні статистичні залежності.
Великі й ефективні нейронні мережі вимагають значних обчислювальних ресурсів.[217] У той час як мозок має апаратне забезпечення, ідеально пристосоване для задачі обробки сигналів графом нейронів, імітація навіть спрощеного нейрону на архітектурі фон Неймана може споживати величезну кількість пам'яті та дискового простору. Крім того, розробникові часто потрібно передавати сигнали багатьма цими з'єднаннями та пов'язаними з ними нейронами, що вимагає величезної обчислювальної потужності та часу ЦП.
Шмідхубер зазначив, що відродження нейронних мереж у двадцять першому сторіччі значною мірою обумовлено досягненнями в апаратному забезпеченні: з 1991 до 2015 року обчислювальна потужність, особливо забезпечувана ГПЗП (на ГП), зросла приблизно в мільйон разів, зробивши стандартний алгоритм зворотного поширення придатним для навчання мереж, на кілька рівнів глибших, ніж раніше.[21] Використання прискорювачів, таких як ПКВМ та ГП, може скорочувати тривалість тренування з місяців до днів. [217]
Нейроморфна інженерія або фізична нейронна мережа[en] розв'язує проблему апаратного забезпечення безпосередньо, створюючи мікросхеми, відмінні від фон нейманових, для безпосереднього втілення нейронних мереж у схемах. Ще одна мікросхема, оптимізована для обробки нейронних мереж, зветься тензорним процесором або ТП (англ. Tensor Processing Unit, TPU).[218]
Аналізувати те, чого навчилася ШНМ, набагато легше, ніж аналізувати те, чого навчилася біологічна нейронна мережа. Крім того, дослідники, які беруть участь у пошуку алгоритмів навчання для нейронних мереж, поступово розкривають загальні принципи, що дозволяють машині, що вчиться, бути успішною. Наприклад, локальне й нелокальне навчання, та неглибока й глибока архітектура.[219]
Прибічники гібридних[en] моделей (що поєднують нейронні мережі та символьні підходи) стверджують, що така суміш може краще вловлювати механізми людського розуму.[220]
-
Одношарова штучна нейронна мережа прямого поширення. Стрілки, що виходять з , для наочності опущено. Є p входів до цієї мережі, й q виходів. У цій системі значення q-того виходу обчислюватиметься як .
-
Двошарова штучна нейронна мережа прямого поширення.
-
Штучна нейронна мережа.
-
Граф залежностей ШНМ.
-
Одношарова штучна нейронна мережа прямого поширення з 4 входами, 6 прихованими вузлами, та 2 виходами. Для заданого стану положення та напряму виводить значення керування для коліс.
-
Двошарова штучна нейронна мережа прямого поширення з 8 входами, 2×8 прихованими вузлами, та 2 виходами. Для заданого стану положення, напряму та інших змінних середовища, видає значення керування для маневрових двигунів.
- Автокодувальник
- ADALINE
- Біологічно натхнені обчислення[en]
- Гіпервимірні обчислення[en]
- Границі великої ширини нейронних мереж[en]
- Катастрофічна інтерференція[en]
- Квантова нейронна мережа
- Когнітивна архітектура[en]
- Конективістська експертна система[en]
- Конектоміка[en]
- Нейронний газ
- Оптична нейронна мережа
- Паралельно розподілена обробка
- Поняття машинного навчання[en]
- Проєкт Blue Brain
- Програмне забезпечення нейронних мереж[en]
- Рекурентні нейронні мережі
- Спайкова нейронна мережа[en]
- Стохастичний папуга[en]
- Тензорно-добуткова мережа[en]
- Філософія штучного інтелекту
- ↑ Для керування «Без рук через Америку[en]» 1995-го року знадобилося «лише кілька випадків людської допомоги».
- ↑ Hardesty, Larry (14 квітня 2017). Explained: Neural networks. MIT News Office. Процитовано 2 червня 2022. (англ.)
- ↑ Yang, Z.R.; Yang, Z. (2014). Comprehensive Biomedical Physics. Karolinska Institute, Stockholm, Sweden: Elsevier. с. 1. ISBN 978-0-444-53633-4. Архів оригіналу за 28 липня 2022. Процитовано 28 липня 2022. (англ.)
- ↑ Mansfield Merriman, "A List of Writings Relating to the Method of Least Squares" (англ.)
- ↑ Stigler, Stephen M. (1981). Gauss and the Invention of Least Squares. Ann. Stat. 9 (3): 465—474. doi:10.1214/aos/1176345451. (англ.)
- ↑ Bretscher, Otto (1995). Linear Algebra With Applications (вид. 3rd). Upper Saddle River, NJ: Prentice Hall. (англ.)
- ↑ а б в г д е ж и к л м н п Schmidhuber, Juergen (2022). Annotated History of Modern AI and Deep Learning. arXiv:2212.11279 [cs.NE]. (англ.)
- ↑ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge: Harvard. ISBN 0-674-40340-1. (англ.)
- ↑ Brush, Stephen G. (1967). History of the Lenz-Ising Model. Reviews of Modern Physics. 39 (4): 883—893. Bibcode:1967RvMP...39..883B. doi:10.1103/RevModPhys.39.883. (англ.)
- ↑ Amari, Shun-Ichi (1972). Learning patterns and pattern sequences by self-organizing nets of threshold elements. IEEE Transactions. C (21): 1197—1206. (англ.)
- ↑ Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences. 79 (8): 2554—2558. Bibcode:1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. PMC 346238. PMID 6953413. (англ.)
- ↑ McCulloch, Warren; Walter Pitts (1943). A Logical Calculus of Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics. 5 (4): 115—133. doi:10.1007/BF02478259. (англ.)
- ↑ Kleene, S.C. (1956). Representation of Events in Nerve Nets and Finite Automata. Annals of Mathematics Studies. № 34. Princeton University Press. с. 3—41. Процитовано 17 червня 2017. (англ.)
- ↑ Hebb, Donald (1949). The Organization of Behavior. New York: Wiley. ISBN 978-1-135-63190-1. (англ.)
- ↑ Farley, B.G.; W.A. Clark (1954). Simulation of Self-Organizing Systems by Digital Computer. IRE Transactions on Information Theory. 4 (4): 76—84. doi:10.1109/TIT.1954.1057468. (англ.)
- ↑ Haykin (2008) Neural Networks and Learning Machines, 3rd edition (англ.)
- ↑ Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model For Information Storage And Organization in the Brain. Psychological Review. 65 (6): 386—408. CiteSeerX 10.1.1.588.3775. doi:10.1037/h0042519. PMID 13602029. S2CID 12781225. (англ.)
- ↑ Werbos, P.J. (1975). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. (англ.)
- ↑ Rosenblatt, Frank (1957). The Perceptron—a perceiving and recognizing automaton. Report 85-460-1. Cornell Aeronautical Laboratory. (англ.)
- ↑ Olazaran, Mikel (1996). A Sociological Study of the Official History of the Perceptrons Controversy. Social Studies of Science. 26 (3): 611—659. doi:10.1177/030631296026003005. JSTOR 285702. S2CID 16786738. (англ.)
- ↑ Minsky, Marvin; Papert, Seymour (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press. ISBN 978-0-262-63022-1. (англ.)
- ↑ а б в Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural Networks. 61: 85—117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. PMID 25462637. S2CID 11715509. (англ.)
- ↑ Ivakhnenko, A. G. (1973). Cybernetic Predicting Devices. CCM Information Corporation. (англ.)
- ↑ Ivakhnenko, A. G.; Lapa, Valentin Grigorʹevich (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co. (англ.)
- ↑ Robbins, H.; Monro, S. (1951). A Stochastic Approximation Method. The Annals of Mathematical Statistics. 22 (3): 400. doi:10.1214/aoms/1177729586. (англ.)
- ↑ Amari, Shun'ichi (1967). A theory of adaptive pattern classifier. IEEE Transactions. EC (16): 279—307. (англ.)
- ↑ а б Kohonen, Teuvo; Honkela, Timo (2007). Kohonen Network. Scholarpedia. 2 (1): 1568. Bibcode:2007SchpJ...2.1568K. doi:10.4249/scholarpedia.1568. (англ.)
- ↑ Kohonen, Teuvo (1982). Self-Organized Formation of Topologically Correct Feature Maps. Biological Cybernetics. 43 (1): 59—69. doi:10.1007/bf00337288. S2CID 206775459. (англ.)
- ↑ Von der Malsburg, C (1973). Self-organization of orientation sensitive cells in the striate cortex. Kybernetik. 14 (2): 85—100. doi:10.1007/bf00288907. PMID 4786750. S2CID 3351573. (англ.)
- ↑ Fukushima, Kunihiko (1980). Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position (PDF). Biological Cybernetics. 36 (4): 193—202. doi:10.1007/BF00344251. PMID 7370364. S2CID 206775608. Процитовано 16 листопада 2013. (англ.)
- ↑ Fukushima, K. (1969). Visual feature extraction by a multilayered network of analog threshold elements. IEEE Transactions on Systems Science and Cybernetics. 5 (4): 322—333. doi:10.1109/TSSC.1969.300225. (англ.)
- ↑ Ramachandran, Prajit; Barret, Zoph; Quoc, V. Le (16 жовтня 2017). Searching for Activation Functions. arXiv:1710.05941 [cs.NE]. (англ.)
- ↑ Leibniz, Gottfried Wilhelm Freiherr von (1920). The Early Mathematical Manuscripts of Leibniz: Translated from the Latin Texts Published by Carl Immanuel Gerhardt with Critical and Historical Notes (Leibniz published the chain rule in a 1676 memoir) (англ.). Open court publishing Company. (англ.)
- ↑ Linnainmaa, Seppo (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors (Masters) (фін.). University of Helsinki. с. 6—7.
- ↑ Linnainmaa, Seppo (1976). Taylor expansion of the accumulated rounding error. BIT Numerical Mathematics. 16 (2): 146—160. doi:10.1007/bf01931367. S2CID 122357351. (англ.)
- ↑ Griewank, Andreas (2012). Who Invented the Reverse Mode of Differentiation?. Optimization Stories. Documenta Matematica, Extra Volume ISMP. с. 389—400. S2CID 15568746. (англ.)
- ↑ Griewank, Andreas; Walther, Andrea (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition. SIAM. ISBN 978-0-89871-776-1. (англ.)
- ↑ Rosenblatt, Frank (1962). Principles of Neurodynamics. Spartan, New York. (англ.)
- ↑ Kelley, Henry J. (1960). Gradient theory of optimal flight paths. ARS Journal. 30 (10): 947—954. doi:10.2514/8.5282. (англ.)
- ↑ A gradient method for optimizing multi-stage allocation processes. Proceedings of the Harvard Univ. Symposium on digital computers and their applications. April 1961. (англ.)
- ↑ а б в Schmidhuber, Jürgen (2015). Deep Learning. Scholarpedia. 10 (11): 85—117. Bibcode:2015SchpJ..1032832S. doi:10.4249/scholarpedia.32832. (англ.)
- ↑ Dreyfus, Stuart E. (1 вересня 1990). Artificial neural networks, back propagation, and the Kelley-Bryson gradient procedure. Journal of Guidance, Control, and Dynamics. 13 (5): 926—928. Bibcode:1990JGCD...13..926D. doi:10.2514/3.25422. ISSN 0731-5090. (англ.)
- ↑ Mizutani, E.; Dreyfus, S.E.; Nishio, K. (2000). On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application. Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium. IEEE: 167–172 vol.2. doi:10.1109/ijcnn.2000.857892. ISBN 0-7695-0619-4. S2CID 351146. (англ.)
- ↑ Dreyfus, Stuart (1973). The computational solution of optimal control problems with time lag. IEEE Transactions on Automatic Control. 18 (4): 383—385. doi:10.1109/tac.1973.1100330. (англ.)
- ↑ Werbos, Paul (1982). Applications of advances in nonlinear sensitivity analysis (PDF). System modeling and optimization. Springer. с. 762—770. Архів (PDF) оригіналу за 14 квітня 2016. Процитовано 2 липня 2017. (англ.)
- ↑ David E. Rumelhart, Geoffrey E. Hinton & Ronald J. Williams, "Learning representations by back-propagating errors [Архівовано 8 березня 2021 у Wayback Machine.]," Nature', 323, pages 533–536 1986. (англ.)
- ↑ Waibel, Alex (December 1987). Phoneme Recognition Using Time-Delay Neural Networks. Meeting of the Institute of Electrical, Information and Communication Engineers (IEICE). Tokyo, Japan. (англ.)
- ↑ Alexander Waibel[en] et al., Phoneme Recognition Using Time-Delay Neural Networks IEEE Transactions on Acoustics, Speech, and Signal Processing, Volume 37, No. 3, pp. 328. – 339 March 1989. (англ.)
- ↑ Zhang, Wei (1988). Shift-invariant pattern recognition neural network and its optical architecture. Proceedings of Annual Conference of the Japan Society of Applied Physics. (англ.)
- ↑ Zhang, Wei (1990). Parallel distributed processing model with local space-invariant interconnections and its optical architecture. Applied Optics. 29 (32): 4790—7. Bibcode:1990ApOpt..29.4790Z. doi:10.1364/AO.29.004790. PMID 20577468. (англ.)
- ↑ LeCun et al., "Backpropagation Applied to Handwritten Zip Code Recognition," Neural Computation, 1, pp. 541–551, 1989. (англ.)
- ↑ J. Weng, N. Ahuja and T. S. Huang, "Cresceptron: a self-organizing neural network which grows adaptively [Архівовано 21 вересня 2017 у Wayback Machine.]," Proc. International Joint Conference on Neural Networks, Baltimore, Maryland, vol I, pp. 576–581, June 1992. (англ.)
- ↑ J. Weng, N. Ahuja and T. S. Huang, "Learning recognition and segmentation of 3-D objects from 2-D images [Архівовано 21 вересня 2017 у Wayback Machine.]," Proc. 4th International Conf. Computer Vision, Berlin, Germany, pp. 121–128, May 1993. (англ.)
- ↑ J. Weng, N. Ahuja and T. S. Huang, "Learning recognition and segmentation using the Cresceptron [Архівовано 25 січня 2021 у Wayback Machine.]," International Journal of Computer Vision, vol. 25, no. 2, pp. 105–139, Nov. 1997. (англ.)
- ↑ LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). Gradient-based learning applied to document recognition (PDF). Proceedings of the IEEE. 86 (11): 2278—2324. CiteSeerX 10.1.1.32.9552. doi:10.1109/5.726791. S2CID 14542261. Процитовано 7 жовтня 2016. (англ.)
- ↑ Qian, Ning, and Terrence J. Sejnowski. "Predicting the secondary structure of globular proteins using neural network models." Journal of molecular biology 202, no. 4 (1988): 865-884. (англ.)
- ↑ Bohr, Henrik, Jakob Bohr, Søren Brunak, Rodney MJ Cotterill, Benny Lautrup, Leif Nørskov, Ole H. Olsen, and Steffen B. Petersen. "Protein secondary structure and homology by neural networks The α-helices in rhodopsin." FEBS letters 241, (1988): 223-228 (англ.)
- ↑ Rost, Burkhard, and Chris Sander. "Prediction of protein secondary structure at better than 70% accuracy." Journal of molecular biology 232, no. 2 (1993): 584-599. (англ.)
- ↑ а б Schmidhuber, Jürgen (1992). Learning complex, extended sequences using the principle of history compression (PDF). Neural Computation. 4 (2): 234—242. doi:10.1162/neco.1992.4.2.234. S2CID 18271205.
{{cite journal}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) (англ.) - ↑ Клейн, О. М. (2023). Метод та засоби виявлення аномалій в кіберфізичних системах комп’ютерного зору (кваліфікаційна робота магістра) (укр.). Хмельницький: Хмельницький національний університет.
- ↑ Schmidhuber, Jürgen (1993). Habilitation Thesis (PDF).
{{cite book}}: Обслуговування CS1: Сторінки з параметром url-status, але без параметра archive-url (посилання) (англ.) - ↑ Schmidhuber, Jürgen (1 листопада 1992). Learning to control fast-weight memories: an alternative to recurrent nets. Neural Computation. 4 (1): 131—139. doi:10.1162/neco.1992.4.1.131. S2CID 16683347. (англ.)
- ↑ а б Schlag, Imanol; Irie, Kazuki; Schmidhuber, Jürgen (2021). Linear Transformers Are Secretly Fast Weight Programmers. ICML 2021. Springer. с. 9355—9366. (англ.)
- ↑ Choromanski, Krzysztof; Likhosherstov, Valerii; Dohan, David; Song, Xingyou; Gane, Andreea; Sarlos, Tamas; Hawkins, Peter; Davis, Jared; Mohiuddin, Afroz; Kaiser, Lukasz; Belanger, David; Colwell, Lucy; Weller, Adrian (2020). Rethinking Attention with Performers. arXiv:2009.14794 [cs.CL]. (англ.)
- ↑ Schmidhuber, Jürgen (1993). Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets. ICANN 1993. Springer. с. 460—463. (англ.)
- ↑ Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N.; Kaiser, Lukasz; Polosukhin, Illia (12 червня 2017). Attention Is All You Need. arXiv:1706.03762 [cs.CL]. (англ.)
- ↑ Wolf, Thomas; Debut, Lysandre; Sanh, Victor; Chaumond, Julien; Delangue, Clement; Moi, Anthony; Cistac, Pierric; Rault, Tim; Louf, Remi; Funtowicz, Morgan; Davison, Joe; Shleifer, Sam; von Platen, Patrick; Ma, Clara; Jernite, Yacine; Plu, Julien; Xu, Canwen; Le Scao, Teven; Gugger, Sylvain; Drame, Mariama; Lhoest, Quentin; Rush, Alexander (2020). Transformers: State-of-the-Art Natural Language Processing. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations. с. 38—45. doi:10.18653/v1/2020.emnlp-demos.6. S2CID 208117506. (англ.)
- ↑ He, Cheng (31 грудня 2021). Transformer in CV. Transformer in CV. Towards Data Science. (англ.)
- ↑ Schmidhuber, Jürgen (1991). A possibility for implementing curiosity and boredom in model-building neural controllers. Proc. SAB'1991. MIT Press/Bradford Books. с. 222—227. (англ.)
- ↑ Schmidhuber, Jürgen (2010). Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990-2010). IEEE Transactions on Autonomous Mental Development. 2 (3): 230—247. doi:10.1109/TAMD.2010.2056368. S2CID 234198. (англ.)
- ↑ Schmidhuber, Jürgen (2020). Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991). Neural Networks (англ.). 127: 58—66. arXiv:1906.04493. doi:10.1016/j.neunet.2020.04.008. PMID 32334341. S2CID 216056336. (англ.)
- ↑ а б Goodfellow, Ian; Pouget-Abadie, Jean; Mirza, Mehdi; Xu, Bing; Warde-Farley, David; Ozair, Sherjil; Courville, Aaron; Bengio, Yoshua (2014). Generative Adversarial Networks (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). с. 2672—2680. Архів (PDF) оригіналу за 22 листопада 2019. Процитовано 20 серпня 2019. (англ.)
- ↑ Prepare, Don't Panic: Synthetic Media and Deepfakes. witness.org. Архів оригіналу за 2 грудня 2020. Процитовано 25 листопада 2020. (англ.)
- ↑ GAN 2.0: NVIDIA's Hyperrealistic Face Generator. SyncedReview.com. 14 грудня 2018. Процитовано 3 жовтня 2019. (англ.)
- ↑ Karras, Tero; Aila, Timo; Laine, Samuli; Lehtinen, Jaakko (1 жовтня 2017). Progressive Growing of GANs for Improved Quality, Stability, and Variation. arXiv:1710.10196. (англ.)
- ↑ а б S. Hochreiter., "Untersuchungen zu dynamischen neuronalen Netzen [Архівовано 2015-03-06 у Wayback Machine.]," Diploma thesis. Institut f. Informatik, Technische Univ. Munich. Advisor: J. Schmidhuber, 1991. (нім.)
- ↑ Hochreiter, S. та ін. (15 січня 2001). Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. У Kolen, John F.; Kremer, Stefan C. (ред.). A Field Guide to Dynamical Recurrent Networks. John Wiley & Sons. ISBN 978-0-7803-5369-5. (англ.)
- ↑ Hochreiter, Sepp; Schmidhuber, Jürgen (1 листопада 1997). Long Short-Term Memory. Neural Computation. 9 (8): 1735—1780. doi:10.1162/neco.1997.9.8.1735. ISSN 0899-7667. PMID 9377276. S2CID 1915014. (англ.)
- ↑ Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural Networks. 61: 85—117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. (англ.)
- ↑ Gers, Felix; Schmidhuber, Jürgen; Cummins, Fred (1999). Learning to forget: Continual prediction with LSTM. 9th International Conference on Artificial Neural Networks: ICANN '99. Т. 1999. с. 850—855. doi:10.1049/cp:19991218. ISBN 0-85296-721-7. (англ.)
- ↑ Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (2 травня 2015). Highway Networks. arXiv:1505.00387 [cs.LG]. (англ.)
- ↑ Srivastava, Rupesh K; Greff, Klaus; Schmidhuber, Juergen (2015). Training Very Deep Networks. Advances in Neural Information Processing Systems. Curran Associates, Inc. 28: 2377—2385. (англ.)
- ↑ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, US: IEEE. с. 770—778. arXiv:1512.03385. doi:10.1109/CVPR.2016.90. ISBN 978-1-4673-8851-1. (англ.)
- ↑ Mead, Carver A.; Ismail, Mohammed (8 травня 1989). Analog VLSI Implementation of Neural Systems (PDF). The Kluwer International Series in Engineering and Computer Science. Т. 80. Norwell, MA: Kluwer Academic Publishers[en]. doi:10.1007/978-1-4613-1639-8. ISBN 978-1-4613-1639-8. Архів оригіналу за 6 листопада 2019. Процитовано 24 січня 2020. (англ.)
- ↑ Domingos, Pedro (22 September 2015). chapter 4. The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World. Basic Books. ISBN 978-0465065707. (англ.)
- ↑ Smolensky, P. (1986). Information processing in dynamical systems: Foundations of harmony theory.. У D. E. Rumelhart; J. L. McClelland; PDP Research Group (ред.). Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Т. 1. с. 194–281. ISBN 978-0-262-68053-0. (англ.)
- ↑ Ng, Andrew; Dean, Jeff (2012). Building High-level Features Using Large Scale Unsupervised Learning. arXiv:1112.6209 [cs.LG]. (англ.)
- ↑ Ian Goodfellow and Yoshua Bengio and Aaron Courville (2016). Deep Learning. MIT Press. Архів оригіналу за 16 квітня 2016. Процитовано 1 червня 2016. (англ.)
- ↑ Cireşan, Dan Claudiu; Meier, Ueli; Gambardella, Luca Maria; Schmidhuber, Jürgen (21 вересня 2010). Deep, Big, Simple Neural Nets for Handwritten Digit Recognition. Neural Computation. 22 (12): 3207—3220. arXiv:1003.0358. doi:10.1162/neco_a_00052. ISSN 0899-7667. PMID 20858131. S2CID 1918673. (англ.)
- ↑ Dominik Scherer, Andreas C. Müller, and Sven Behnke: "Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition [Архівовано 3 квітня 2018 у Wayback Machine.]," In 20th International Conference Artificial Neural Networks (ICANN), pp. 92–101, 2010. DOI:10.1007/978-3-642-15825-4_10. (англ.)
- ↑ Інтерв'ю Kurzweil AI 2012 року [Архівовано 31 серпня 2018 у Wayback Machine.] з Юргеном Шмідхубером про вісім змагань, виграних його командою Глибокого навчання в 2009—2012 роках (англ.)
- ↑ How bio-inspired deep learning keeps winning competitions | KurzweilAI. www.kurzweilai.net. Архів оригіналу за 31 серпня 2018. Процитовано 16 червня 2017. (англ.)
- ↑ а б Graves, Alex; Schmidhuber, Jürgen (2009). Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks (PDF). У Koller, D.; Schuurmans, Dale; Bengio, Yoshua; Bottou, L. (ред.). Advances in Neural Information Processing Systems 21 (NIPS 2008). Neural Information Processing Systems (NIPS) Foundation. с. 545—552. ISBN 9781605609492. (англ.)
- ↑ а б Graves, A.; Liwicki, M.; Fernandez, S.; Bertolami, R.; Bunke, H.; Schmidhuber, J. (May 2009). A Novel Connectionist System for Unconstrained Handwriting Recognition (PDF). IEEE Transactions on Pattern Analysis and Machine Intelligence. 31 (5): 855—868. CiteSeerX 10.1.1.139.4502. doi:10.1109/tpami.2008.137. ISSN 0162-8828. PMID 19299860. S2CID 14635907. Архів (PDF) оригіналу за 2 січня 2014. Процитовано 30 липня 2014. (англ.)
- ↑ Ciresan, Dan; Meier, U.; Schmidhuber, J. (June 2012). Multi-column deep neural networks for image classification. с. 3642—3649. arXiv:1202.2745. Bibcode:2012arXiv1202.2745C. CiteSeerX 10.1.1.300.3283. doi:10.1109/cvpr.2012.6248110. ISBN 978-1-4673-1228-8. S2CID 2161592.
{{cite book}}: Проігноровано|journal=(довідка) (англ.) - ↑ а б Zell, Andreas (2003). chapter 5.2. Simulation neuronaler Netze [Simulation of Neural Networks] (нім.) (вид. 1st). Addison-Wesley. ISBN 978-3-89319-554-1. OCLC 249017987. (нім.)
- ↑ Artificial intelligence (вид. 3rd). Addison-Wesley Pub. Co. 1992. ISBN 0-201-53377-4. (англ.)
- ↑ Abbod, Maysam F. (2007). Application of Artificial Intelligence to the Management of Urological Cancer. The Journal of Urology. 178 (4): 1150—1156. doi:10.1016/j.juro.2007.05.122. PMID 17698099. (англ.)
- ↑ Dawson, Christian W. (1998). An artificial neural network approach to rainfall-runoff modelling. Hydrological Sciences Journal. 43 (1): 47—66. doi:10.1080/02626669809492102. (англ.)
- ↑ The Machine Learning Dictionary. www.cse.unsw.edu.au. Архів оригіналу за 26 серпня 2018. Процитовано 4 листопада 2009. (англ.)
- ↑ Ciresan, Dan; Ueli Meier; Jonathan Masci; Luca M. Gambardella; Jurgen Schmidhuber (2011). Flexible, High Performance Convolutional Neural Networks for Image Classification (PDF). Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence-Volume Volume Two. 2: 1237—1242. Архів (PDF) оригіналу за 5 квітня 2022. Процитовано 7 липня 2022. (англ.)
- ↑ Zell, Andreas (1994). Simulation Neuronaler Netze [Simulation of Neural Networks] (нім.) (вид. 1st). Addison-Wesley. с. 73. ISBN 3-89319-554-8.
- ↑ Miljanovic, Milos (February–March 2012). Comparative analysis of Recurrent and Finite Impulse Response Neural Networks in Time Series Prediction (PDF). Indian Journal of Computer and Engineering. 3 (1). (англ.)
- ↑ Lau, Suki (10 липня 2017). A Walkthrough of Convolutional Neural Network – Hyperparameter Tuning. Medium. Архів оригіналу за 4 лютого 2023. Процитовано 23 серпня 2019. (англ.)
- ↑ Kelleher, John D.; Mac Namee, Brian; D'Arcy, Aoife (2020). 7-8. Fundamentals of machine learning for predictive data analytics: algorithms, worked examples, and case studies (вид. 2nd). Cambridge, MA. ISBN 978-0-262-36110-1. OCLC 1162184998. (англ.)
- ↑ Wei, Jiakai (26 квітня 2019). Forget the Learning Rate, Decay Loss. arXiv:1905.00094 [cs.LG]. (англ.)
- ↑ Li, Y.; Fu, Y.; Li, H.; Zhang, S. W. (1 червня 2009). The Improved Training Algorithm of Back Propagation Neural Network with Self-adaptive Learning Rate. Т. 1. с. 73—76. doi:10.1109/CINC.2009.111. ISBN 978-0-7695-3645-3. S2CID 10557754.
{{cite book}}: Проігноровано|journal=(довідка) (англ.) - ↑ Huang, Guang-Bin; Zhu, Qin-Yu; Siew, Chee-Kheong (2006). Extreme learning machine: theory and applications. Neurocomputing. 70 (1): 489—501. CiteSeerX 10.1.1.217.3692. doi:10.1016/j.neucom.2005.12.126. S2CID 116858. (англ.)
- ↑ Widrow, Bernard та ін. (2013). The no-prop algorithm: A new learning algorithm for multilayer neural networks. Neural Networks. 37: 182—188. doi:10.1016/j.neunet.2012.09.020. PMID 23140797. (англ.)
- ↑ Ollivier, Yann; Charpiat, Guillaume (2015). Training recurrent networks without backtracking. arXiv:1507.07680 [cs.NE]. (англ.)
- ↑ Hinton, G. E. (2010). A Practical Guide to Training Restricted Boltzmann Machines. Tech. Rep. UTML TR 2010-003. Архів оригіналу за 9 травня 2021. Процитовано 27 червня 2017. (англ.)
- ↑ ESANN. 2009.
- ↑ Bernard, Etienne (2021). Introduction to machine learning (англ.). Champaign. с. 9. ISBN 978-1579550486. Процитовано 22 березня 2023.
- ↑ а б в г Синєглазов, Віктор; Чумаченко, Олена (2022). Бідюк, П. І.; Шугалей, Л. П. (ред.). Методи та технології напівкерованого навчання: Курс лекцій (PDF) (укр.). Київ: НТУУ «КПІ ім. Ігоря Сікорського».
- ↑ а б в г Дуда, О. М.; Кунанець, Н. Е.; Мацюк, О. В.; Пасічник, В. В. (21—27 травня 2018). Методи аналітичного опрацювання big data (PDF). Інтелектуальні системи прийняття рішень та проблеми обчислювального інтелекту (укр.). Залізний Порт. с. 159. ISBN 978-617-7573-17-2.
- ↑ а б в г Кропивницька, В. Б.; Магас, Д. М. (30 квітня 2023). Напівкероване машинне навчання для виявлення несправностей нафтогазопроводів. Modern engineering and innovative technologies (укр.). 1 (18): 33—36. doi:10.30890/2567-5273.2023-26-01-010.
- ↑ Bernard, Etienne (2021). Introduction to machine learning (англ.). Champaign. с. 12. ISBN 978-1579550486. Процитовано 22 березня 2023.
- ↑ а б В'юненко, О. Б.; Виганяйло, С. М. (12 травня 2021). Сокуренко, В. В.; Швець, Д. В.; Могілевський, Л. В.; Шульга, В. П.; Яковлєв, Р. П.; Шмельов, Ю. М. (ред.). Інновації та загальні проблеми підвищення рівня кібербезпеки (PDF). II Міжнародна науково-практична конференція «Авіація, промисловість, суспільство» (укр.). Т. 1. МВС України, Харківський національний університет внутрішніх справ, Кременчуцький льотний коледж. с. 169. ISBN 978-966-610-243-3.
- ↑ Bernard, Etienne (2021). Introduction to Machine Learning. Wolfram Media Inc. с. 9. ISBN 978-1-579550-48-6. (англ.)
- ↑ Хорошилов, С. В.; Редька, М. О. (2019). Інтелектуальне керування орієнтацією космічних апаратів із використанням навчання з підкріпленням (PDF). Технічна механіка (укр.). Дніпро: Інститут технічної механіки Національної академії наук України та Державного космічного агентства України (4). doi:10.15407/itm2019.04.029.
- ↑ Ojha, Varun Kumar; Abraham, Ajith; Snášel, Václav (1 квітня 2017). Metaheuristic design of feedforward neural networks: A review of two decades of research. Engineering Applications of Artificial Intelligence. 60: 97—116. arXiv:1705.05584. Bibcode:2017arXiv170505584O. doi:10.1016/j.engappai.2017.01.013. S2CID 27910748. (англ.)
- ↑ Dominic, S.; Das, R.; Whitley, D.; Anderson, C. (July 1991). Genetic reinforcement learning for neural networks. IJCNN-91-Seattle International Joint Conference on Neural Networks. IJCNN-91-Seattle International Joint Conference on Neural Networks. Seattle, Washington, US: IEEE. с. 71—76. doi:10.1109/IJCNN.1991.155315. ISBN 0-7803-0164-1. (англ.)
- ↑ Hoskins, J.C.; Himmelblau, D.M. (1992). Process control via artificial neural networks and reinforcement learning. Computers & Chemical Engineering. 16 (4): 241—251. doi:10.1016/0098-1354(92)80045-B. (англ.)
- ↑ Bertsekas, D.P.; Tsitsiklis, J.N. (1996). Neuro-dynamic programming. Athena Scientific. с. 512. ISBN 978-1-886529-10-6. Архів оригіналу за 29 червня 2017. Процитовано 17 червня 2017. (англ.)
- ↑ Secomandi, Nicola (2000). Comparing neuro-dynamic programming algorithms for the vehicle routing problem with stochastic demands. Computers & Operations Research. 27 (11–12): 1201—1225. CiteSeerX 10.1.1.392.4034. doi:10.1016/S0305-0548(99)00146-X. (англ.)
- ↑ de Rigo, D.; Rizzoli, A. E.; Soncini-Sessa, R.; Weber, E.; Zenesi, P. (2001). Neuro-dynamic programming for the efficient management of reservoir networks. Proceedings of MODSIM 2001, International Congress on Modelling and Simulation. MODSIM 2001, International Congress on Modelling and Simulation. Canberra, Australia: Modelling and Simulation Society of Australia and New Zealand. doi:10.5281/zenodo.7481. ISBN 0-86740-525-2. Архів оригіналу за 7 August 2013. Процитовано 29 July 2013. (англ.)
- ↑ Damas, M.; Salmeron, M.; Diaz, A.; Ortega, J.; Prieto, A.; Olivares, G. (2000). Genetic algorithms and neuro-dynamic programming: application to water supply networks. Proceedings of 2000 Congress on Evolutionary Computation. 2000 Congress on Evolutionary Computation. Т. 1. La Jolla, California, US: IEEE. с. 7—14. doi:10.1109/CEC.2000.870269. ISBN 0-7803-6375-2. (англ.)
- ↑ Deng, Geng; Ferris, M.C. (2008). Neuro-dynamic programming for fractionated radiotherapy planning. Springer Optimization and Its Applications. Т. 12. с. 47—70. CiteSeerX 10.1.1.137.8288. doi:10.1007/978-0-387-73299-2_3. ISBN 978-0-387-73298-5. (англ.)
- ↑ Bozinovski, S. (1982). "A self-learning system using secondary reinforcement". In R. Trappl (ed.) Cybernetics and Systems Research: Proceedings of the Sixth European Meeting on Cybernetics and Systems Research. North Holland. pp. 397–402. ISBN 978-0-444-86488-8. (англ.)
- ↑ Bozinovski, S. (2014) "Modeling mechanisms of cognition-emotion interaction in artificial neural networks, since 1981 [Архівовано 23 березня 2019 у Wayback Machine.]." Procedia Computer Science p. 255-263 (англ.)
- ↑ Bozinovski, Stevo; Bozinovska, Liljana (2001). Self-learning agents: A connectionist theory of emotion based on crossbar value judgment. Cybernetics and Systems. 32 (6): 637—667. doi:10.1080/01969720118145. S2CID 8944741. (англ.)
- ↑ Welcoming the Era of Deep Neuroevolution. Uber Blog. 18 грудня 2017. Процитовано 15 квітня 2023. (англ.)
- ↑ Artificial intelligence can 'evolve' to solve problems. Science | AAAS. 10 січня 2018. Архів оригіналу за 9 грудня 2021. Процитовано 7 лютого 2018. (англ.)
- ↑ Turchetti, Claudio (2004), Stochastic Models of Neural Networks, Frontiers in artificial intelligence and applications: Knowledge-based intelligent engineering systems, т. 102, IOS Press, ISBN 9781586033880 (англ.)
- ↑ Jospin, Laurent Valentin; Laga, Hamid; Boussaid, Farid; Buntine, Wray; Bennamoun, Mohammed (2022). Hands-On Bayesian Neural Networks—A Tutorial for Deep Learning Users. IEEE Computational Intelligence Magazine. 17 (2): 29—48. arXiv:2007.06823. doi:10.1109/mci.2022.3155327. ISSN 1556-603X. S2CID 220514248. Архів оригіналу за 4 лютого 2023. Процитовано 19 листопада 2022. (англ.)
- ↑ de Rigo, D.; Castelletti, A.; Rizzoli, A. E.; Soncini-Sessa, R.; Weber, E. (January 2005). A selective improvement technique for fastening Neuro-Dynamic Programming in Water Resources Network Management. У Pavel Zítek (ред.). Proceedings of the 16th IFAC World Congress – IFAC-PapersOnLine. 16th IFAC World Congress. Т. 16. Prague, Czech Republic: IFAC. с. 7—12. doi:10.3182/20050703-6-CZ-1902.02172. hdl:11311/255236. ISBN 978-3-902661-75-3. Архів оригіналу за 26 квітня 2012. Процитовано 30 грудня 2011. (англ.)
- ↑ Ferreira, C. (2006). Designing Neural Networks Using Gene Expression Programming. У A. Abraham; B. de Baets; M. Köppen; B. Nickolay (ред.). Applied Soft Computing Technologies: The Challenge of Complexity (PDF). Springer-Verlag. с. 517—536. Архів (PDF) оригіналу за 19 грудня 2013. Процитовано 8 жовтня 2012. (англ.)
- ↑ Da, Y.; Xiurun, G. (July 2005). An improved PSO-based ANN with simulated annealing technique. У T. Villmann (ред.). New Aspects in Neurocomputing: 11th European Symposium on Artificial Neural Networks. Т. 63. Elsevier. с. 527—533. doi:10.1016/j.neucom.2004.07.002. Архів оригіналу за 25 квітня 2012. Процитовано 30 грудня 2011. (англ.)
- ↑ Wu, J.; Chen, E. (May 2009). A Novel Nonparametric Regression Ensemble for Rainfall Forecasting Using Particle Swarm Optimization Technique Coupled with Artificial Neural Network. У Wang, H.; Shen, Y.; Huang, T.; Zeng, Z. (ред.). 6th International Symposium on Neural Networks, ISNN 2009. Lecture Notes in Computer Science. Т. 5553. Springer. с. 49—58. doi:10.1007/978-3-642-01513-7_6. ISBN 978-3-642-01215-0. Архів оригіналу за 31 грудня 2014. Процитовано 1 січня 2012. (англ.)
- ↑ а б Ting Qin; Zonghai Chen; Haitao Zhang; Sifu Li; Wei Xiang; Ming Li (2004). A learning algorithm of CMAC based on RLS (PDF). Neural Processing Letters. 19 (1): 49—61. doi:10.1023/B:NEPL.0000016847.18175.60. S2CID 6233899. Архів (PDF) оригіналу за 14 квітня 2021. Процитовано 30 січня 2019. (англ.)
- ↑ Ting Qin; Haitao Zhang; Zonghai Chen; Wei Xiang (2005). Continuous CMAC-QRLS and its systolic array (PDF). Neural Processing Letters. 22 (1): 1—16. doi:10.1007/s11063-004-2694-0. S2CID 16095286. Архів (PDF) оригіналу за 18 листопада 2018. Процитовано 30 січня 2019. (англ.)
- ↑ LeCun Y, Boser B, Denker JS, Henderson D, Howard RE, Hubbard W, Jackel LD (1989). Backpropagation Applied to Handwritten Zip Code Recognition. Neural Computation. 1 (4): 541—551. doi:10.1162/neco.1989.1.4.541. S2CID 41312633. (англ.)
- ↑ Yann LeCun (2016). Slides on Deep Learning Online [Архівовано 23 квітня 2016 у Wayback Machine.] (англ.)
- ↑ Hochreiter, Sepp; Schmidhuber, Jürgen (1 листопада 1997). Long Short-Term Memory. Neural Computation. 9 (8): 1735—1780. doi:10.1162/neco.1997.9.8.1735. ISSN 0899-7667. PMID 9377276. S2CID 1915014. (англ.)
- ↑ Sak, Hasim; Senior, Andrew; Beaufays, Francoise (2014). Long Short-Term Memory recurrent neural network architectures for large scale acoustic modeling (PDF). Архів оригіналу (PDF) за 24 квітня 2018. (англ.)
- ↑ Li, Xiangang; Wu, Xihong (15 жовтня 2014). Constructing Long Short-Term Memory based Deep Recurrent Neural Networks for Large Vocabulary Speech Recognition. arXiv:1410.4281 [cs.CL]. (англ.)
- ↑ Fan, Y.; Qian, Y.; Xie, F.; Soong, F. K. (2014). TTS synthesis with bidirectional LSTM based Recurrent Neural Networks. Proceedings of the Annual Conference of the International Speech Communication Association, Interspeech: 1964—1968. Процитовано 13 червня 2017. (англ.)
- ↑ Zen, Heiga; Sak, Hasim (2015). Unidirectional Long Short-Term Memory Recurrent Neural Network with Recurrent Output Layer for Low-Latency Speech Synthesis (PDF). Google.com. ICASSP. с. 4470—4474. Архів (PDF) оригіналу за 9 травня 2021. Процитовано 27 червня 2017. (англ.)
- ↑ Fan, Bo; Wang, Lijuan; Soong, Frank K.; Xie, Lei (2015). Photo-Real Talking Head with Deep Bidirectional LSTM (PDF). Proceedings of ICASSP. Архів (PDF) оригіналу за 1 листопада 2017. Процитовано 27 червня 2017. (англ.)
- ↑ Silver, David; Hubert, Thomas; Schrittwieser, Julian; Antonoglou, Ioannis; Lai, Matthew; Guez, Arthur; Lanctot, Marc; Sifre, Laurent; Kumaran, Dharshan; Graepel, Thore; Lillicrap, Timothy; Simonyan, Karen; Hassabis, Demis (5 грудня 2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815 [cs.AI]. (англ.)
- ↑ Zoph, Barret; Le, Quoc V. (4 листопада 2016). Neural Architecture Search with Reinforcement Learning. arXiv:1611.01578 [cs.LG]. (англ.)
- ↑ Haifeng Jin; Qingquan Song; Xia Hu (2019). Auto-keras: An efficient neural architecture search system. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM. arXiv:1806.10282. Архів оригіналу за 21 серпня 2019. Процитовано 21 серпня 2019 — через autokeras.com. (англ.)
- ↑ Claesen, Marc; De Moor, Bart (2015). Hyperparameter Search in Machine Learning. arXiv:1502.02127 [cs.LG]. Bibcode: 2015arXiv150202127C (англ.)
- ↑ Probst, Philipp; Boulesteix, Anne‐Laure; Bischl, Bernd (26 лютого 2018). Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 20: 53:1–53:32. S2CID 88515435. Процитовано 18 березня 2023. (англ.)
- ↑ Zou, Jinming; Han, Yi; So, Sung-Sau (2009). Artificial Neural Networks: Methods and Applications. Methods in Molecular Biology. Т. 458 (вид. Livingstone, David J.). Totowa, NJ: Humana Press. с. 15—23. doi:10.1007/978-1-60327-101-1_2. ISBN 978-1-60327-101-1. PMID 19065803. Процитовано 18 березня 2023. (англ.)
- ↑ Esch, Robin (1990). Handbook of Applied Mathematics: Selected Results and Methods (вид. Springer US). Boston, MA: Springer US. с. 928—987. doi:10.1007/978-1-4684-1423-3_17. ISBN 978-1-4684-1423-3. Процитовано 18 березня 2023. (англ.)
- ↑ Sarstedt, Marko; Moo, Erik (2019). Regression Analysis. A Concise Guide to Market Research. Springer Texts in Business and Economics. Springer Berlin Heidelberg. с. 209—256. doi:10.1007/978-3-662-56707-4_7. ISBN 978-3-662-56706-7. S2CID 240396965. (англ.)
- ↑ Tian, Jie; Tan, Yin; Sun, Chaoli; Zeng, Jianchao; Jin, Yaochu (December 2016). A self-adaptive similarity-based fitness approximation for evolutionary optimization. 2016 IEEE Symposium Series on Computational Intelligence (SSCI): 1—8. doi:10.1109/SSCI.2016.7850209. ISBN 978-1-5090-4240-1. S2CID 14948018. (англ.)
- ↑ Turek, Fred D. (March 2007). Introduction to Neural Net Machine Vision. Vision Systems Design. 12 (3). Архів оригіналу за 16 травня 2013. Процитовано 5 березня 2013. (англ.)
- ↑ Alaloul, Wesam Salah; Qureshi, Abdul Hannan (2019). Data Processing Using Artificial Neural Networks. Dynamic Data Assimilation - Beating the Uncertainties. doi:10.5772/intechopen.91935. ISBN 978-1-83968-083-0. S2CID 219735060. (англ.)
- ↑ Pal, Madhab; Roy, Rajib; Basu, Joyanta; Bepari, Milton S. (2013). Blind source separation: A review and analysis. 2013 International Conference Oriental COCOSDA held jointly with 2013 Conference on Asian Spoken Language Research and Evaluation (O-COCOSDA/CASLRE). IEEE. с. 1—5. doi:10.1109/ICSDA.2013.6709849. ISBN 978-1-4799-2378-6. S2CID 37566823. (англ.)
- ↑ Zissis, Dimitrios (October 2015). A cloud based architecture capable of perceiving and predicting multiple vessel behaviour. Applied Soft Computing. 35: 652—661. doi:10.1016/j.asoc.2015.07.002. Архів оригіналу за 26 липня 2020. Процитовано 18 липня 2019. (англ.)
- ↑ Roman M. Balabin; Ekaterina I. Lomakina (2009). Neural network approach to quantum-chemistry data: Accurate prediction of density functional theory energies. J. Chem. Phys. 131 (7): 074104. Bibcode:2009JChPh.131g4104B. doi:10.1063/1.3206326. PMID 19708729. (англ.)
- ↑ Silver, David та ін. (2016). Mastering the game of Go with deep neural networks and tree search (PDF). Nature. 529 (7587): 484—489. Bibcode:2016Natur.529..484S. doi:10.1038/nature16961. PMID 26819042. S2CID 515925. Архів (PDF) оригіналу за 23 листопада 2018. Процитовано 31 січня 2019. (англ.)
- ↑ Sengupta, Nandini; Sahidullah, Md; Saha, Goutam (August 2016). Lung sound classification using cepstral-based statistical features. Computers in Biology and Medicine. 75 (1): 118—129. doi:10.1016/j.compbiomed.2016.05.013. PMID 27286184. (англ.)
- ↑ Choy, Christopher B., et al. "3d-r2n2: A unified approach for single and multi-view 3d object reconstruction [Архівовано 26 липня 2020 у Wayback Machine.]." European conference on computer vision. Springer, Cham, 2016. (англ.)
- ↑ Gessler, Josef (August 2021). Sensor for food analysis applying impedance spectroscopy and artificial neural networks. RiuNet UPV (1): 8—12. Архів оригіналу за 21 жовтня 2021. Процитовано 21 жовтня 2021. (англ.)
- ↑ Maitra, D. S.; Bhattacharya, U.; Parui, S. K. (August 2015). CNN based common approach to handwritten character recognition of multiple scripts. 2015 13th International Conference on Document Analysis and Recognition (ICDAR): 1021—1025. doi:10.1109/ICDAR.2015.7333916. ISBN 978-1-4799-1805-8. S2CID 25739012. (англ.)
- ↑ French, Jordan (2016). The time traveller's CAPM. Investment Analysts Journal. 46 (2): 81—96. doi:10.1080/10293523.2016.1255469. S2CID 157962452. (англ.)
- ↑ Schechner, Sam (15 червня 2017). Facebook Boosts A.I. to Block Terrorist Propaganda. The Wall Street Journal. ISSN 0099-9660. Процитовано 16 червня 2017. (англ.)
- ↑ Ganesan, N (2010). Application of Neural Networks in Diagnosing Cancer Disease Using Demographic Data. International Journal of Computer Applications. 1 (26): 81—97. Bibcode:2010IJCA....1z..81G. doi:10.5120/476-783. (англ.)
- ↑ Bottaci, Leonardo (1997). Artificial Neural Networks Applied to Outcome Prediction for Colorectal Cancer Patients in Separate Institutions (PDF). Lancet. The Lancet. 350 (9076): 469—72. doi:10.1016/S0140-6736(96)11196-X. PMID 9274582. S2CID 18182063. Архів оригіналу (PDF) за 23 листопада 2018. Процитовано 2 травня 2012. (англ.)
- ↑ Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). Measuring systematic changes in invasive cancer cell shape using Zernike moments. Integrative Biology. 8 (11): 1183—1193. doi:10.1039/C6IB00100A. PMID 27735002. (англ.)
- ↑ Lyons, Samanthe (2016). Changes in cell shape are correlated with metastatic potential in murine. Biology Open. 5 (3): 289—299. doi:10.1242/bio.013409. PMC 4810736. PMID 26873952. (англ.)
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (28 серпня 2017). Deep Learning for Accelerated Reliability Analysis of Infrastructure Networks. Computer-Aided Civil and Infrastructure Engineering. 33 (6): 443—458. arXiv:1708.08551. Bibcode:2017arXiv170808551N. doi:10.1111/mice.12359. S2CID 36661983. (англ.)
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (2018). Accelerating Stochastic Assessment of Post-Earthquake Transportation Network Connectivity via Machine-Learning-Based Surrogates. Transportation Research Board 97th Annual Meeting. Архів оригіналу за 9 березня 2018. Процитовано 14 березня 2018. (англ.)
- ↑ Díaz, E.; Brotons, V.; Tomás, R. (September 2018). Use of artificial neural networks to predict 3-D elastic settlement of foundations on soils with inclined bedrock. Soils and Foundations. 58 (6): 1414—1422. Bibcode:2018SoFou..58.1414D. doi:10.1016/j.sandf.2018.08.001. hdl:10045/81208. ISSN 0038-0806. (англ.)
- ↑ Tayebiyan, A.; Mohammad, T. A.; Ghazali, A. H.; Mashohor, S. Artificial Neural Network for Modelling Rainfall-Runoff. Pertanika Journal of Science & Technology. 24 (2): 319—330. (англ.)
- ↑ Govindaraju, Rao S. (1 квітня 2000). Artificial Neural Networks in Hydrology. I: Preliminary Concepts. Journal of Hydrologic Engineering. 5 (2): 115—123. doi:10.1061/(ASCE)1084-0699(2000)5:2(115). (англ.)
- ↑ Govindaraju, Rao S. (1 квітня 2000). Artificial Neural Networks in Hydrology. II: Hydrologic Applications. Journal of Hydrologic Engineering. 5 (2): 124—137. doi:10.1061/(ASCE)1084-0699(2000)5:2(124). (англ.)
- ↑ Peres, D. J.; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. (1 жовтня 2015). Significant wave height record extension by neural networks and reanalysis wind data. Ocean Modelling. 94: 128—140. Bibcode:2015OcMod..94..128P. doi:10.1016/j.ocemod.2015.08.002. (англ.)
- ↑ Dwarakish, G. S.; Rakshith, Shetty; Natesan, Usha (2013). Review on Applications of Neural Network in Coastal Engineering. Artificial Intelligent Systems and Machine Learning. 5 (7): 324—331. Архів оригіналу за 15 серпня 2017. Процитовано 5 липня 2017. (англ.)
- ↑ Ermini, Leonardo; Catani, Filippo; Casagli, Nicola (1 березня 2005). Artificial Neural Networks applied to landslide susceptibility assessment. Geomorphology. Geomorphological hazard and human impact in mountain environments. 66 (1): 327—343. Bibcode:2005Geomo..66..327E. doi:10.1016/j.geomorph.2004.09.025. (англ.)
- ↑ Nix, R.; Zhang, J. (May 2017). Classification of Android apps and malware using deep neural networks. 2017 International Joint Conference on Neural Networks (IJCNN): 1871—1878. doi:10.1109/IJCNN.2017.7966078. ISBN 978-1-5090-6182-2. S2CID 8838479. (англ.)
- ↑ Detecting Malicious URLs. The systems and networking group at UCSD. Архів оригіналу за 14 липня 2019. Процитовано 15 лютого 2019. (англ.)
- ↑ Homayoun, Sajad; Ahmadzadeh, Marzieh; Hashemi, Sattar; Dehghantanha, Ali; Khayami, Raouf (2018), Dehghantanha, Ali; Conti, Mauro; Dargahi, Tooska (ред.), BoTShark: A Deep Learning Approach for Botnet Traffic Detection, Cyber Threat Intelligence, Advances in Information Security, Springer International Publishing, с. 137—153, doi:10.1007/978-3-319-73951-9_7, ISBN 978-3-319-73951-9 (англ.)
- ↑ Ghosh та Reilly (January 1994). Credit card fraud detection with a neural-network. 1994 Proceedings of the Twenty-Seventh Hawaii International Conference on System Sciences. 3: 621—630. doi:10.1109/HICSS.1994.323314. ISBN 978-0-8186-5090-1. S2CID 13260377. (англ.)
- ↑ Ananthaswamy, Anil (19 квітня 2021). Latest Neural Nets Solve World's Hardest Equations Faster Than Ever Before. Quanta Magazine. Процитовано 12 травня 2021. (англ.)
- ↑ AI has cracked a key mathematical puzzle for understanding our world. MIT Technology Review. Процитовано 19 листопада 2020. (англ.)
- ↑ Caltech Open-Sources AI for Solving Partial Differential Equations. InfoQ. Архів оригіналу за 25 січня 2021. Процитовано 20 січня 2021. (англ.)
- ↑ Nagy, Alexandra (28 червня 2019). Variational Quantum Monte Carlo Method with a Neural-Network Ansatz for Open Quantum Systems. Physical Review Letters. 122 (25): 250501. arXiv:1902.09483. Bibcode:2019PhRvL.122y0501N. doi:10.1103/PhysRevLett.122.250501. PMID 31347886. S2CID 119074378. (англ.)
- ↑ Yoshioka, Nobuyuki; Hamazaki, Ryusuke (28 червня 2019). Constructing neural stationary states for open quantum many-body systems. Physical Review B. 99 (21): 214306. arXiv:1902.07006. Bibcode:2019PhRvB..99u4306Y. doi:10.1103/PhysRevB.99.214306. S2CID 119470636. (англ.)
- ↑ Hartmann, Michael J.; Carleo, Giuseppe (28 червня 2019). Neural-Network Approach to Dissipative Quantum Many-Body Dynamics. Physical Review Letters. 122 (25): 250502. arXiv:1902.05131. Bibcode:2019PhRvL.122y0502H. doi:10.1103/PhysRevLett.122.250502. PMID 31347862. S2CID 119357494. (англ.)
- ↑ Vicentini, Filippo; Biella, Alberto; Regnault, Nicolas; Ciuti, Cristiano (28 червня 2019). Variational Neural-Network Ansatz for Steady States in Open Quantum Systems. Physical Review Letters. 122 (25): 250503. arXiv:1902.10104. Bibcode:2019PhRvL.122y0503V. doi:10.1103/PhysRevLett.122.250503. PMID 31347877. S2CID 119504484. (англ.)
- ↑ Forrest MD (April 2015). Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs >400 times faster. BMC Neuroscience. 16 (27): 27. doi:10.1186/s12868-015-0162-6. PMC 4417229. PMID 25928094.
{{cite journal}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) (англ.) - ↑ Siegelmann, H.T.; Sontag, E.D. (1991). Turing computability with neural nets (PDF). Appl. Math. Lett. 4 (6): 77—80. doi:10.1016/0893-9659(91)90080-F. (англ.)
- ↑ Bains, Sunny (3 листопада 1998). Analog computer trumps Turing model. EE Times. Процитовано 11 травня 2023. (англ.)
- ↑ Balcázar, José (July 1997). Computational Power of Neural Networks: A Kolmogorov Complexity Characterization. IEEE Transactions on Information Theory. 43 (4): 1175—1183. CiteSeerX 10.1.1.411.7782. doi:10.1109/18.605580. (англ.)
- ↑ Надригайло, Т.Ж.; Молчанова, К.А. (2011). Аналіз нейронних алгоритмів (PDF). Мат. мод. 2 (25): 5—6 (50—51).
- ↑ Демчук, О.С. (2019). Робоча програма навчальної дисципліни «Нейронні мережі та нейро-нечіткі технології» (PDF). Рівне: НУВГП. Процитовано 4 червня 2023.
- ↑ а б MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. ISBN 978-0-521-64298-9. Архів (PDF) оригіналу за 19 October 2016. Процитовано 11 June 2016. (англ.)
- ↑ Cover, Thomas (1965). Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition (PDF). IEEE Transactions on Electronic Computers. IEEE. EC-14 (3): 326—334. doi:10.1109/PGEC.1965.264137. Архів (PDF) оригіналу за 5 березня 2016. Процитовано 10 березня 2020. (англ.)
- ↑ Gerald, Friedland (2019). Reproducibility and Experimental Design for Machine Learning on Audio and Multimedia Data. MM '19: Proceedings of the 27th ACM International Conference on Multimedia. ACM: 2709—2710. doi:10.1145/3343031.3350545. ISBN 978-1-4503-6889-6. S2CID 204837170. (англ.)
- ↑ Stop tinkering, start measuring! Predictable experimental design of Neural Network experiments. The Tensorflow Meter. Архів оригіналу за 18 April 2022. Процитовано 10 March 2020. (англ.)
- ↑ Lee, Jaehoon; Xiao, Lechao; Schoenholz, Samuel S.; Bahri, Yasaman; Novak, Roman; Sohl-Dickstein, Jascha; Pennington, Jeffrey (2020). Wide neural networks of any depth evolve as linear models under gradient descent. Journal of Statistical Mechanics: Theory and Experiment. 2020 (12): 124002. arXiv:1902.06720. Bibcode:2020JSMTE2020l4002L. doi:10.1088/1742-5468/abc62b. S2CID 62841516. (англ.)
- ↑ Arthur Jacot; Franck Gabriel; Clement Hongler (2018). Neural Tangent Kernel: Convergence and Generalization in Neural Networks (PDF). 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, Canada. Архів (PDF) оригіналу за 22 червня 2022. Процитовано 4 червня 2022. (англ.)
- ↑ Xu ZJ, Zhang Y, Xiao Y (2019). Training Behavior of Deep Neural Network in Frequency Domain. У Gedeon T, Wong K, Lee M (ред.). Neural Information Processing. ICONIP 2019. Lecture Notes in Computer Science. Т. 11953. Springer, Cham. с. 264—274. arXiv:1807.01251. doi:10.1007/978-3-030-36708-4_22. ISBN 978-3-030-36707-7. S2CID 49562099. (англ.)
- ↑ Nasim Rahaman; Aristide Baratin; Devansh Arpit; Felix Draxler; Min Lin; Fred Hamprecht; Yoshua Bengio; Aaron Courville (2019). On the Spectral Bias of Neural Networks (PDF). Proceedings of the 36th International Conference on Machine Learning. 97: 5301—5310. arXiv:1806.08734. Архів (PDF) оригіналу за 22 жовтня 2022. Процитовано 4 червня 2022. (англ.)
- ↑ Zhi-Qin John Xu; Yaoyu Zhang; Tao Luo; Yanyang Xiao; Zheng Ma (2020). Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks. Communications in Computational Physics. 28 (5): 1746—1767. arXiv:1901.06523. Bibcode:2020CCoPh..28.1746X. doi:10.4208/cicp.OA-2020-0085. S2CID 58981616. (англ.)
- ↑ Tao Luo; Zheng Ma; Zhi-Qin John Xu; Yaoyu Zhang (2019). Theory of the Frequency Principle for General Deep Neural Networks. arXiv:1906.09235 [cs.LG]. (англ.)
- ↑ Xu, Zhiqin John; Zhou, Hanxu (18 травня 2021). Deep Frequency Principle Towards Understanding Why Deeper Learning Is Faster. Proceedings of the AAAI Conference on Artificial Intelligence. 35 (12): 10541—10550. arXiv:2007.14313. doi:10.1609/aaai.v35i12.17261. ISSN 2374-3468. S2CID 220831156. Архів оригіналу за 5 жовтня 2021. Процитовано 5 жовтня 2021. (англ.)
- ↑ Parisi, German I.; Kemker, Ronald; Part, Jose L.; Kanan, Christopher; Wermter, Stefan (1 травня 2019). Continual lifelong learning with neural networks: A review. Neural Networks. 113: 54—71. doi:10.1016/j.neunet.2019.01.012. ISSN 0893-6080. PMID 30780045. (англ.)
- ↑ Dewdney, A. K. (1 квітня 1997). Yes, we have no neutrons: an eye-opening tour through the twists and turns of bad science. Wiley. с. 82. ISBN 978-0-471-10806-1. (англ.)
- ↑ NASA – Dryden Flight Research Center – News Room: News Releases: NASA NEURAL NETWORK PROJECT PASSES MILESTONE [Архівовано 2 квітня 2010 у Wayback Machine.]. Nasa.gov. Retrieved on 20 November 2013. (англ.)
- ↑ Roger Bridgman's defence of neural networks. Архів оригіналу за 19 березня 2012. Процитовано 12 липня 2010. (англ.)
- ↑ D. J. Felleman and D. C. Van Essen, "Distributed hierarchical processing in the primate cerebral cortex," Cerebral Cortex, 1, pp. 1–47, 1991. (англ.)
- ↑ J. Weng, "Natural and Artificial Intelligence: Introduction to Computational Brain-Mind," BMI Press, ISBN 978-0-9858757-2-5, 2012. (англ.)
- ↑ а б Edwards, Chris (25 червня 2015). Growing pains for deep learning. Communications of the ACM. 58 (7): 14—16. doi:10.1145/2771283. S2CID 11026540. (англ.)
- ↑ Cade Metz (18 травня 2016). Google Built Its Very Own Chips to Power Its AI Bots. Wired. Архів оригіналу за 13 січня 2018. Процитовано 5 березня 2017. (англ.)
- ↑ Scaling Learning Algorithms towards AI (PDF). Архів (PDF) оригіналу за 12 серпня 2022. Процитовано 6 липня 2022. (англ.)
- ↑ Tahmasebi; Hezarkhani (2012). A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Computers & Geosciences. 42: 18—27. Bibcode:2012CG.....42...18T. doi:10.1016/j.cageo.2012.02.004. PMC 4268588. PMID 25540468. (англ.)
- Bhadeshia H. K. D. H. (1999). Neural Networks in Materials Science (PDF). ISIJ International. 39 (10): 966—979. doi:10.2355/isijinternational.39.966. (англ.)
- Bishop, Christopher M. (1995). Neural networks for pattern recognition. Clarendon Press. ISBN 978-0-19-853849-3. OCLC 33101074. (англ.)
- Borgelt, Christian (2003). Neuro-Fuzzy-Systeme : von den Grundlagen künstlicher Neuronaler Netze zur Kopplung mit Fuzzy-Systemen. Vieweg. ISBN 978-3-528-25265-6. OCLC 76538146. (нім.)
- Cybenko, G.V. (2006). Approximation by Superpositions of a Sigmoidal function. У van Schuppen, Jan H. (ред.). Mathematics of Control, Signals, and Systems. Springer International. с. 303—314. PDF (англ.)
- Dewdney, A. K. (1997). Yes, we have no neutrons : an eye-opening tour through the twists and turns of bad science. New York: Wiley. ISBN 978-0-471-10806-1. OCLC 35558945. (англ.)
- Duda, Richard O.; Hart, Peter Elliot; Stork, David G. (2001). Pattern classification (вид. 2). Wiley. ISBN 978-0-471-05669-0. OCLC 41347061. (англ.)
- Egmont-Petersen, M.; de Ridder, D.; Handels, H. (2002). Image processing with neural networks – a review. Pattern Recognition. 35 (10): 2279—2301. CiteSeerX 10.1.1.21.5444. doi:10.1016/S0031-3203(01)00178-9. (англ.)
- Fahlman, S.; Lebiere, C (1991). The Cascade-Correlation Learning Architecture (PDF). Архів оригіналу (PDF) за 3 травня 2013. Процитовано 28 серпня 2006. (англ.)
- created for National Science Foundation, Contract Number EET-8716324, and Defense Advanced Research Projects Agency (DOD), ARPA Order No. 4976 under Contract F33615-87-C-1499.
- Gurney, Kevin (1997). An introduction to neural networks. UCL Press. ISBN 978-1-85728-673-1. OCLC 37875698. (англ.)
- Haykin, Simon S. (1999). Neural networks : a comprehensive foundation. Prentice Hall. ISBN 978-0-13-273350-2. OCLC 38908586. (англ.)
- Hertz, J.; Palmer, Richard G.; Krogh, Anders S. (1991). Introduction to the theory of neural computation. Addison-Wesley. ISBN 978-0-201-51560-2. OCLC 21522159. (англ.)
- Information theory, inference, and learning algorithms. Cambridge University Press. 25 вересня 2003. Bibcode:2003itil.book.....M. ISBN 978-0-521-64298-9. OCLC 52377690. (англ.)
- Kruse, Rudolf; Borgelt, Christian; Klawonn, F.; Moewes, Christian; Steinbrecher, Matthias; Held, Pascal (2013). Computational intelligence : a methodological introduction. Springer. ISBN 978-1-4471-5012-1. OCLC 837524179. (англ.)
- Lawrence, Jeanette (1994). Introduction to neural networks : design, theory and applications. California Scientific Software. ISBN 978-1-883157-00-5. OCLC 32179420. (англ.)
- MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. ISBN 978-0-521-64298-9. (англ.)
- Masters, Timothy (1994). Signal and image processing with neural networks : a C++ sourcebook. J. Wiley. ISBN 978-0-471-04963-0. OCLC 29877717. (англ.)
- Maurer, Harald (2021). Cognitive science : integrative synchronization mechanisms in cognitive neuroarchitectures of the modern connectionism. CRC Press. doi:10.1201/9781351043526. ISBN 978-1-351-04352-6. S2CID 242963768. (англ.)
- Ripley, Brian D. (2007). Pattern Recognition and Neural Networks. Cambridge University Press. ISBN 978-0-521-71770-0. (англ.)
- Siegelmann, H.T.; Sontag, Eduardo D. (1994). Analog computation via neural networks. Theoretical Computer Science. 131 (2): 331—360. doi:10.1016/0304-3975(94)90178-3. S2CID 2456483. (англ.)
- Smith, Murray (1993). Neural networks for statistical modeling. Van Nostrand Reinhold. ISBN 978-0-442-01310-3. OCLC 27145760. (англ.)
- Wasserman, Philip D. (1993). Advanced methods in neural computing. Van Nostrand Reinhold. ISBN 978-0-442-00461-3. OCLC 27429729. (англ.)
- Wilson, Halsey (2018). Artificial intelligence. Grey House Publishing. ISBN 978-1-68217-867-6. (англ.)
| ||||||||||||||||||||||||||||||||||||||||
|




![{\displaystyle \textstyle C=E[(x-f(x))^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2929ecb1606fdfeaddc55477d9671e11c034e21c)











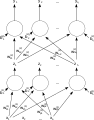
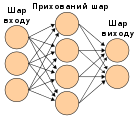



![Паралельно-конвеєрна структура нейронної мережі АКММ[en]. Цей алгоритм навчання здатен збігатися за один крок.](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6d/Cmac.jpg/177px-Cmac.jpg)