Теорема Ролля
| Вибрані статті із |
| Числення |
|---|
|
|
|
Спеціалізоване |

У диференціальному та інтегральному численні теорема Ролля, або лема Ролля, стверджує, що будь-яка дійснозначна диференційовна функція, яка досягає рівних значень у двох різних точках, повинна мати принаймні одну стаціонарну точку між ними — тобто точку, де перша похідна (кутовий коефіцієнт дотичної до графіка функції) дорівнює нулю. Теорема названа на честь Мішеля Ролля[en].
Формулювання[ред. | ред. код]
Нехай функція неперервна на проміжку , диференційована в усіх внутрішніх точках проміжку . Нехай, окрім того, . Тоді на проміжку знайдеться принаймні одна точка така, що значення похідної у цій точці дорівнює нулю.
Доведення[ред. | ред. код]
Оскільки функція неперервна на проміжку , то, згідно з другою теоремою Вейєрштрасса, ця функція досягає на ньому свого максимального значення та мінімального значення . Отже, маємо два випадки:
- ;
- ;
У першому випадку . Тому похідна дорівнює нулю в будь-якій точці проміжку .
У випадку, коли , оскільки , можна стверджувати, що хоча б одне з двох значень чи досягається функцією в деякій внутрішній точці проміжку . Але тоді функція має у точці локальний екстремум. Оскільки функція диференційовна в точці , то за необхідною умовою локального екстремуму, .
Історія[ред. | ред. код]
Індійському математику Бхаскару II (1114—1185) приписують знання теореми Ролля[1]. Хоча теорема названа на честь Мішеля Ролля[en], доведення Ролля 1691 року охоплює лише випадок поліноміальних функцій. Його доведення не використовувало методи диференціального числення, які на той момент свого життя він вважав хибними. Теорема вперше була доведена Коші в 1823 році як наслідок доведення теореми Лагранжа[2]. Назва «теорема Ролля» була вперше використана Морицем Вільгельмом Дробішем[en] в Німеччині в 1834 році та Джусто Беллавітісом[en] в Італії в 1846 році[3].
Приклади[ред. | ред. код]
Перший приклад[ред. | ред. код]
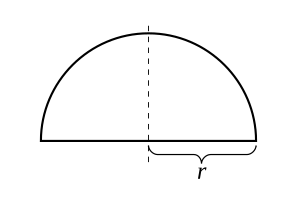
Для радіуса розглянемо функцію
Графіком цієї функції є верхнє півколо з центром у початку координат. Функція неперервна на закритому інтервалі і диференційовна на відкритому інтервалі , але не диференційовна на кінцевих точках і . Оскільки , то можна використовувати теорему Ролля, і дійсно, є точка де похідна від функції дорівнює нулю. Зауважимо, що теорему можна використовувати навіть тоді, коли функція не є диференційовною у кінцевих точках, оскільки вимагається, щоб вона була диференційовною лише на відкритому інтервалі.
Другий приклад[ред. | ред. код]

Якщо диференційовність порушується у внутрішній точці інтервалу, то теореми Ролля може не виконуватися. Розглянемо функцію модуля
Тут , але між та не існує такого для якого . Це тому, що ця функція, хоча і неперервна, але не є диференційовною при . Зауважимо, що похідна від функції змінює знак у точці , але без досягнення нульового значення. Теорему не можна застосувати до цієї функції тому, що вона не задовольняє умову того, що функція повинна бути диференційовною для будь-якого з відкритого інтервалу. Однак, якщо вимогу диференційовності виключити з теореми Ролля, то функція може мати критичну точку на відкритому інтервалі , але не матиме горизонтальної дотичної (як у випадку функції модуля, що зображена на рисунку).
Узагальнення[ред. | ред. код]
Другий приклад ілюструє наступне узагальнення теореми Ролля: Розглянемо дійснозначну, неперервну функцію на закритому інтервалі з . Якщо для будь-якого на відкритому інтервалі існують правостороння границя
і лівостороння границя
- — на розширеній дійсній прямій , тоді існує деяке число на відкритому інтервалі таке, що одна з двох границь
є , а інша (на розширеній дійсній прямій). Якщо ліво- і правостороння границі узгоджуються для будь-якого , тоді вони узгоджуються зокрема для , звідси похідна функції існує у точці і дорівнює нулю.
Зауваження[ред. | ред. код]
- Якщо опукла, або увігнута, тоді ліво- та правосторонні похідні існують у будь-якій внутрішній точці, звідси існують вищенаведені границі і вони є дійсними числами.
- Узагальнена версія теореми є достатнью для доведення опуклості функції, якщо односторонні похідні є монотонно зростаючими:
Доведення узагальненої версії[ред. | ред. код]
Оскільки доведення стандартної версії теореми Ролля та її узагальнення дуже схожі, доведемо тут лише узагальнений варіант.
Ідея доведення полягає в тому, щоб довести, що якщо , тоді функція має досягати максимуму або мінімуму десь між та , скажімо в точці , і функція має із зростаючої стати спадною (або навпаки) у точці . Зокрема, якщо похідна існує вона має дорівнювати нулю в точці .
Згідно припущення функція є неперервною на і за другою теоремою Веєрштрасса досягає максимуму і мінімуму на . Якщо максимум і мінімум досягнуто в кінцевих точках на , тоді є константою на і похідна від функції дорівнює нулю у будь-якій точці на .
Нехай максимум досягається у внутрішній точці на (випадок для мінімуму дуже схожий, лише необхідно розглянути функцію ). Потрібно розглянути вищезазначені право- та лівосторонні границі окремо.
Для дійсного такого, як , значення менше, або рівне , оскільки функція досягає максимуму в точці . Тому, для будь-якого ,
Звідси
де границя існує за припущенням (може дорівнювати мінус нескінченність). Аналогічно, для будь-якого , нерівність змінюється, оскільки знаменник тепер від'ємний, а тому отримуємо
Звідси
де границя може дорівнювати плюс нескінченність.
Нарешті, коли вищезазначені право- та лівостороння границі узгоджуються (зокрема, якщо є диференційованою), тоді похідна від у точці дорівнює нулю. (Як альтернативу, можемо застосувати теорему Ферма).
Узагальнення на випадок похідних вищих порядків[ред. | ред. код]
Теорему Ролля можна узагальнити, вимагаючи, щоб функція мала більше точок з однаковими значеннями і більшу регулярність. Зокрема, нехай
- функція разів неперервно диференційовна на замкненому інтервалі і -на похідна існує на відкритому інтервалі і
- є інтервалів, що визначаються точками на інтервалі , такі що для будь-якого від до .
Тоді тут є число на таке, що -на похідна функції у точці дорівнює нулю.
Вимоги щодо -ї похідної функції можуть бути послаблені, як у вищезазначеному узагальненні, допускаючи аналогічні (можливо слабші) твердження для вищезазначених право- та лівосторонніх границь для функції замість функції .
Зокрема, ця версія теореми стверджує: якщо диференційовна достатньо разів функція має коренів (тобто існує точок у яких функція дорівнює нулю), тоді тут є внутрішня точка де дорівнює нулю.
Узагальнення на інші поля[ред. | ред. код]
Теорема Ролля — властивість диференційовних функцій над полем дійсних чисел, яке є впорядкованим полем. У представленому вигляді вона не узагальнюється на інші поля, але наступне твердження має місце: якщо дійсні поліміальні множники функції (мають всі її корені) над полем дійсних чисел, тоді її похідна також має цю властивість. Можна назвати цю властивість поля — властивістю Ролля. Над більш загальними полями не завжди визначають диференційовні функції, але над ними завжди можна розглядати поліноми, які можна диференціювати у символьній формі. Аналогічним чином, над більш загальні полями не завжди визначені поняття порядку, але над цими полями завжди визначено поняття кореня полінома.
Таким чином, теорема Ролля показує, що поле дійсних чисел має властивість Ролля. Будь-яке алгебраїчно замкнене поле таке, як поле комплексних чисел, має властивість Ролля. Однак, поле раціональних чисел не має цієї властивості. Наприклад, розкладається на множники над полем раціональних чисел, але їх похідна ні:
Питання про те, які поля задовольняють властивості Ролля, було піднято у 1972 році Капланським. Щодо скінченних полів відповідь полягає в тому, що тільки поля та мають властивість Ролля.
Щодо комплексної версії використовують індекс Вурхоува[en].
Геометричний зміст теореми[ред. | ред. код]
Теорема має простий геометричний зміст: якщо кінцеві ординати кривої рівні, то, згідно з теоремою Ролля, на цій кривій знайдеться точка, у якій дотична до кривої паралельна до осі .
Нехай неперервної кривої (тобто образа інтервалу або окружності при неперервному відображенні у площину) у кожній точці існує дотичний вектор. Тоді між двома точками перетину кривої із розділяючим рішенням динамічної системи є тока контакту.
Перетин кривої із розділяючим рішенням є замкненою множиною. Доповнення цієї множини розпадається на (скінченні та нескінченні) інтервали. Кожний скінченний інтервал такого роду містить точку контакту. Нехай та — параметри кінців такого інтервалу, і передує у сенсі орієнтації кривої. Для усіх проміжних значень параметрів крива лежить у області Існує близький момент часу до , у який впорядкована пара векторів, яка складається з дотичного вектора до кривої та вектора динамічної системи, задає ту саму орієнтацію площини, що й за трансверсального входу кривої у область Оберемо локальну систему координат навколо точки кривої із параметром , у якій векторне поле динамічної системи стале. Нехай у цих локальних координатах , область визначається нерівністю динамічна система має вигляд
розділяюче рішення є а крива задається вектор-функцією По умові за (та ) й Тому у деякий момент, близький до , похідна функції буде додатною. У цей момент впорядкована пара векторів задає потрібну орієнтацію площини.
Теорема є справедливою для -гладких кривих, трансверсально перекриваючих розділяюче рішення. Нехай та — параметри двох послідокних трансверсальних перетинів кривої із розділяючих рішенням. Це рішення ділить площину на дві (не обов'язково зв'язні) області: область орієнтованою межею якої воно є, та додаткову область Нехай у момент крива входить до області Тоді у момент крива виходить з області Впорядковані пари векторів, які складаються із дотичного вектора до кривої й вектора динамічної системи, у момент та визначають протилежні орієнтації площини. Відповідно, у деякий проміжний момент дотичний вектор та вектор динамічної системи є колінеарними.
Нехай крива, яка є гладким многовидом на площині, містить не більше ніж некомпактних (і будь-яке число компактних) компонент зв'язності й має не більше ніж точок контакту із динамічною системою. Тоді вона має не більш ніж ізольованих точок перетину із будь-яким розділяючи рішенням цієї системи.
На компактній компоненті точок перетину не більше, ніж точок контакту. На некомпактній — точок перетину може бути на одиницю більше, ніж точок контакту[4].
Примітки[ред. | ред. код]
- ↑ Gupta, R. C. Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. с. 156. Архів оригіналу за 10 грудня 2019. Процитовано 26 травня 2021.
- ↑ Besenyei, A. (17 вересня 2012). A brief history of the mean value theorem (PDF). Архів оригіналу (PDF) за 6 травня 2021. Процитовано 26 травня 2021.
- ↑ See Cajori, Florian. A History of Mathematics. с. 224. Архів оригіналу за 28 листопада 2021. Процитовано 26 травня 2021.
- ↑ Хованский А.Г. - Малочлены.
Література[ред. | ред. код]
- Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
- Завало С. Т. (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа. с. 462. (укр.)
- Ильин В. А., Позняк Э. Г. Основы математического анализа. — 7-е. — М : Физматлит, 2004. — Т. 1. — 644 с. — ISBN 5-9221-0536-1.(рос.)
- Leithold, Louis (1972). The Calculus, with Analytic Geometry (вид. 2nd). New York: Harper & Row. с. 201–207. ISBN 0-06-043959-9.
- Taylor, Angus E. (1955). Advanced Calculus. Boston: Ginn and Company. с. 30—37.
Див. також[ред. | ред. код]
| Вікісховище має мультимедійні дані за темою: Теорема Ролля |
- Друга теорема Веєрштрасса
- Екстремум
- Дотична
- Похідна
- Мішель Ролль[en]
- Карл Вейєрштрасс
- Теорема Лагранжа
- Теорема Больцано-Коші
- Лінійна інтерполяція
- Теорема Гауса — Люка
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (жовтень 2015) |
| Це незавершена стаття з математики. Ви можете допомогти проєкту, виправивши або дописавши її. |

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7ef1f348169f09e9db96b68d4b2e73d5f43c156)
![{\displaystyle [-r,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dbcf3f99b353b618465500fe9576e0850885ffd)




![{\displaystyle f(x)=|x|,\qquad x\in [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106570318bb857ac95a60c075c30a0f40dde84fe)







![{\displaystyle [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13233867b861889693a36843d98e51d90d38f9f)








![{\displaystyle c+h\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77d806861a02acd7905ece257775b9a28f59a71d)













![{\displaystyle [-3,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6759df2a8fdc54833780c7396174381ec7a269f)



























