Відбір вибірки (статистика)

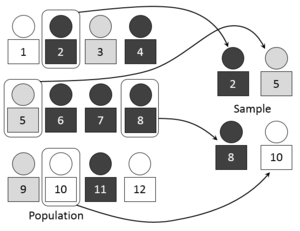
В математичній статистиці, забезпеченні якості, методології опитування відбір вибірки (або вибирання, англ. sampling) — це вибирання підмножини (статистичної вибірки) об'єктів із генеральної сукупності з метою оцінювання характеристик генеральної сукупності в цілому. Двома головними перевагами відбирання є те, що, порівняно з обмірюванням всієї генеральної сукупності, витрати на вибірці є нижчими, і збирання даних є швидшим.

Кожне спостереження є вимірюванням однієї або декількох властивостей (таких як вага, положення, колір) об'єктів спостереження, які розрізняють як незалежні об'єкти або особи. У вибиранні для обстеження^[en], щоби підлаштуватися до дизайну вибирання, зокрема, стратифікованого вибирання, до даних можуть застосовуватися ваги.^[1] Для ведення цієї діяльності застосовуються результати з теорії ймовірностей та теорії статистики. Відбирання широко застосовують для збирання інформації про населення в бізнесових та медичних дослідженнях.^[2] Для визначення того, чи виробнича партія матеріалу відповідає нормативним вимогам, застосовують вибіркове обстежування^[en].

Опис

Метод відбору вибірки також є ефективним для пов'язання статистичних властивостей вибірки з цілями моделювання, число яких може бути досить великим.

Н. Н. Чубуков наводить наступний приклад^[3]. Нехай випадковий процес представлений вибіркою об'єму $N:X(t_{1}),X(t_{2}),...,X(t_{N}).$ Необхідно вирішити три завдання:

Виконати умовно довгостроковий прогноз для $X(t_{N+10});$
Виконати умовно короткостроковий прогноз для $X(t_{N+1});$
Визначити функцію $X=X(t)$ для відновлення значення $X$ в будь-якій точці всередині вибірки

Якщо взяти для моделювання традиційний підхід, орієнтований на єдиність опису статистичних властивостей процесу, то результатом будуть три абсолютно однакові функції. Справа в тому, що правилом розрахунку критерію якості моделі не враховувалися суттєві деталі: глибина прогнозу, характер статистичних трендів випадкового процесу, представленого вибірковими даними, і зовсім ігнорується цільова специфіка завдань.

Принцип різноманітності

Виходом з даного ускладнення може стати використання системного принципу різноманітності. Цей принцип в останні три десятиліття все більш активно впроваджується в інженерні додатки математичної статистики завдяки розробці таких методів перехресної валідації даних, як бутстреп-аналіз, метод групового обліку аргументів^[4] та ін. Прояв принципу різноманітності в рішеннях статистичних задач полягає в тому, що на незнання імовірнісних властивостей вихідних даних алгоритм відповідає різноманітністю моделей, які генеруються, кожна з яких підлягає крос-перевірці за певною єдиною для всіх моделей схемою.

Завдання

Таким чином, відбір вибірки є сучасним методом, який може виявитися ефективним для ряду інженерних додатків математичної статистики, особливо, пов'язаних з розв'язанням обернених задач. Відбір вибірки реалізує принцип різноманітності і може узагальнювати весь спектр засобів статистичного аналізу, заснований на управлінні вихідними даними. Під відбором вибірки розуміється набір прийомів для розділення початкової вибірки на робочі та контрольні ділянки за певними правилами. На робочих ділянках виконується розрахунок параметрів «конкуруючих» моделей, на контрольних оцінюється їх здатність відновлювати значення, які не використовувалися для розрахунку параметрів. Відбір вибірки усуває основну перешкоду, яка об'єктивно присутня в обернених задачах. ЇЇ причина криється у неможливості встановлення строгого математичного зв'язку між варіюючим параметром і величиною критерію. При цьому відбір вибірки автоматично переводить алгоритм структурно-параметричної ідентифікації моделі в розряд евристичних.

Стосовно вищенаведеного прикладу, першому випадку — «довгої» екстраполяції за межі вибірки, відповідає варіант відбору вибірки з виключенням з розрахунків параметрів моделі десяти останніх вибіркових значень поспіль. Контрольним буде десятий відлік. Робоча підвибірка складе всі значення, за винятком цієї десятки. Потім альтернативним перебором визначається найкраща модель, яка точніше інших спрогнозувала контрольну точку. Зміною положення виключених відліків, без порушення їх числа і нерозривності, формується статистика нев'язок, застосовна для розрахунку критерію. Алгоритм як би «екзаменує» моделі екстраполяції на задану глибину, і вибирає з них ту, яка найбільш точно вловлює тренди, які містять інформацію про значення на лагу довжиною в десять відліків.

Другому завданню буде відповідати відбір вибірки з виключенням із розрахунків по одній контрольній точці, з комбінуванням кількості та порядку попередніх значень, які враховуються для прогнозу.

У третьому завданні буде виправдано дроблення вибірки на взаємопроникні блоки, коли контрольні значення «вкраплені» між робітниками. Довжина таких блоків і глибина їх взаємопроникнення повинна враховувати інтервали між сусідніми точками діапазону, необхідні стійкість і точність оцінок. Так, третій задачі може відповідати виключення із розрахунків кожного третього відліку вибірки та застосування виключених даних для контролю з циклічним перепризначенням контрольних і робочих підвибірок.

Переваги

Вибір варіантів вибірки неоднозначний і визначається на основі досвіду і знань оператора про властивості вихідних даних, мети розв'язуваної задачі, а також може підбиратися або уточнюватися експериментально. Кількість прийнятних способів розбиття діапазону на порядки перевершує обсяг вибірки, і дає достатню різноманітність засобів для вираження корисності моделей. Відбір вибірки може виявитися ефективним у вирішенні зворотних задач, оскільки він є:

альтернативою морально застарілого параметричного способу перевірки гіпотез про належність даних теоретичного розподілу;
евристичним і відкритим по відношенню до оператора, вибирає із заданого набору варіант вибору вибірки, відповідний специфіці завдання;
середовищем формування нормованих критеріальних функцій, зручних для моделювання мети, статистичної коригування мети, і кількісно відбиває близькість до неї;
засобом побудови емпіричних розподілів, що дозволяє накопичувати статистику, визначати або уточнювати варіант вибірки та оцінювати достовірність результатів;
економічно перспективним, здатним виділяти найменший достатній для конкретної розв'язуваної задачі набір вибіркових даних з діапазону, що є цікавим з точки зору зниження витрат;
підвищує інтелектуальність систем управління за рахунок надання їм системних властивостей доцільності, цілісності, раціональності, ієрархічності, самоорганізації і достатньої різноманітності.

Види вибірки

Вибірка за значимістю
Вибірка з відхиленням
Районована вибірка
Алгоритм Метрополіса — Гастінгса

Основні підходи: імовірнісного та неімовірнісного відбору

Імовірнісна (випадкова) вибірка: кожен елемент генеральної сукупності має відомий, ненульовий шанс потрапити у вибірку.
Неімовірнісна (невипадкова) вибірка: відбір здійснюється за суб’єктивними або зручними критеріями (доступність, квоти, добровільна участь тощо). Такий підхід може призводити до систематичних зсувів (базис) і не гарантує репрезентативності.

Стандартні методи імовірнісного відбору

Метод	Опис
Проста випадкова вибірка (simple random sampling)	Кожний елемент має однакову ймовірність потрапити у вибірку; вибір здійснюється випадково (наприклад, жеребкування, генератор випадкових чисел).
Стратифікована випадкова вибірка (stratified sampling)	Генеральну сукупність ділять на однорідні за певною ознакою підгрупи (страти), потім з кожної страти відбирають випадкову підвибірку. Це підвищує точність оцінок і знижує вибіркову дисперсію.
Систематична вибірка (systematic sampling)	Має сенс, коли є список (frame) елементів: вибирають випадкову стартову позицію, потім через регулярні інтервали (кожний k-й) відбирають елементи. Це простий і економічний підхід.
Кластерна вибірка (cluster sampling)	Генеральну сукупність ділять на кластери (групи), потім випадковим чином вибирають деякі кластери, і беруть або всі елементи в них (одноетапна), або підвибірку всередині них (багатоетапна). Зручно, коли повний перелік елементів складний чи розрізнений.

Крім цього, застосовують багатоетапну (multistage) вибірку, сніжкову (snowball sampling), резервуарну (reservoir sampling) — особливо при роботі з потоковими даними або «розмитими» сукупностями.

Репрезентативність, оцінка похибок і план вибірки

Репрезентативна вибірка — така, яка «адекватно відображає» властивості генеральної сукупності: розподіл змінних, структуру підгруп, співвідношення тощо. План вибірки — це набір правил, що гарантує репрезентативність.
При стратифікованому відборі часто застосовують пропорційне або оптимальне (наприклад, за Нейманом/Чупровим) розміщення, коли обсяг вибірки у кожній страті залежить не лише від розміру страти, але й від варіабельності ознаки в ній — щоб мінімізувати дисперсію оцінки.
У вибіркових дослідженнях ключове — оцінити похибку і ймовірність того, що вибірка відхиляється від сукупності. Для цього інколи застосовують повторні підвибірки, бутстрепи тощо.
План вибірки має враховувати мету дослідження, доступ до реєстру/переліку, ресурси, очікувану неоднорідність сукупності, імовірну вибіркову помилку та потреби в довірчих інтервалах.

Сучасні підходи: бутстреп, MCMC, гіперпросторова вибірка

У класичному статистичному відборі маємо справу з класичними методами. Проте в сучасних задачах — машинного навчання, інженерії, моделювання — використовують:

Бутстреп-аналіз (bootstrap) — метод повторного випадкового вибору з повтореннями з наявної вибірки, щоб оцінити дисперсію, довірчі інтервали чи стабільність оцінок.
Методи вибірки з розподілу (sampling from distribution) — простий Монте-Карло, важливісна вибірка (importance sampling), а також Метрополіс–Гастінгс алгоритм (Metropolis–Hastings), Gibbs sampling та інші MCMC — коли потрібно згенерувати вибірку з заданого (або приблизного) розподілу.
Стратифікація + латинські гіперквести (Latin hypercube sampling, LHS), або її узагальнення як частково-стратифікована вибірка (PSS), — корисно при моделюванні багатовимірних випадкових величин, щоб краще покрити простір параметрів та зменшити дисперсію оцінок.

Такі методи роблять вибірку гнучкішою, а висновки — більш надійними, особливо в умовах невизначеності про розподіли або при роботі з великими / складними даними.

Приклади застосування

У статистичних обстеженнях населення / підприємств: застосовують стратифіковану або систематичну вибірку для забезпечення репрезентативності. Державна служба статистики України+2Державна служба статистики України+2
У контролі якості та прийманні партій продукції — застосовують Lot quality assurance sampling (LQAS): невелика випадкова підмножина заміряних одиниць, щоб вирішити, чи партія відповідає стандарту. Вікіпедія
У прикладному моделюванні, машинному навчанні, симуляціях — бутстреп, Monte Carlo, MCMC, Latin-hypercube sampling — для оцінки невизначеностей, перевірок моделей, генерації синтетичних даних.

Математичні аспекти вибіркового відбору

У класичній теорії вибірки центральне місце займає поняття функціонала вибірки. Нехай має місце генеральна сукупність зі значеннями випадкової величини X та вибірка обсягу n. Тоді вибіркові характеристики — середнє, дисперсія, медіана, квантилі — розглядаються як випадкові величини, для яких можна досліджувати:

зміщення (bias),
дисперсію (variance),
середньоквадратичну помилку (MSE),
асимптотичні властивості.

Для випадкової вибірки оцінка середнього є незміщеною і має дисперсію σ2/n. Однак для інших методів відбору, наприклад систематичного чи кластерного, дисперсія змінюється і залежить від кореляцій у сукупності. Це робить важливим поняття дизайн-ефекту — коефіцієнта збільшення дисперсії оцінки через особливості плану вибірки.

У стратифікованому відборі дизайн-ефект часто менший 1, що означає кращу ефективність порівняно з простою випадковою вибіркою. У кластерній — як правило більший 1, бо елементи в одному кластері подібні між собою.

Примітки

↑ Lance, P. & Hattori, A. (2016). Sampling and Evaluation. Web: MEASURE Evaluation. с. 6—8, 62—64. Архів оригіналу за 26 листопада 2020. Процитовано 17 липня 2018.
↑ Salant, Priscilla, I. Dillman, and A. Don. How to conduct your own survey. No. 300.723 S3. 1994.
↑ Чубуков Н. Н. Алгоритмизация калибровок мехатронных систем с использованием семплинга // Мехатроника, автоматизация, управление. 2013. № 7.
↑ Ивахненко, 1971.

Література

(рос.)Чубуков Н. Н. Алгоритмизация калибровок мехатронных систем с использованием сэмплинга. Мехатроника, автоматизация, управление. 2013 г., № 7.
(рос.)Эфрон Б. Нетрадиционные методы многомерного статистического анализа: Сб. статей: Пер. с англ./ Предисловие Ю. П. Адлера, Ю. А. Кошевника. — М.: Финансы и статистика, 1988.- 263 с. ил.
(рос.)Ивахненко А. Г. Системы эвристической самоорганизации в технической кибернетике. — Киев: Техника, 1971. — 327 с.
«Methods of Sampling» — онлайн-огляд основних методів відбору.
«Стратифікована, систематична, кластерна вибірка» — українські методичні документи, зокрема від Державна служба статистики України. Державна служба статистики України
«Sampling Algorithms, from Survey Sampling to Monte Carlo Methods: Tutorial and Literature Review» — сучасний огляд статистичних алгоритмів вибірки.
«Statistics in Survey Sampling» (2024) — сучасні теоретичні і прикладні положення вибіркового спостереження.
Стаття про контролю якості: Lot quality assurance sampling (LQAS) як приклад вибіркового контролю дефектів.

[1] Lance, P. & Hattori, A. (2016). Sampling and Evaluation. Web: MEASURE Evaluation. с. 6—8, 62—64. Архів оригіналу за 26 листопада 2020. Процитовано 17 липня 2018.

[2] Salant, Priscilla, I. Dillman, and A. Don. How to conduct your own survey. No. 300.723 S3. 1994.

[3] Чубуков Н. Н. Алгоритмизация калибровок мехатронных систем с использованием семплинга // Мехатроника, автоматизация, управление. 2013. № 7.

[4] Ивахненко, 1971.

[1]

[2]

[3]

[4]