Спонтанне порушення симетрії
| Квантова теорія поля |
|---|
 |
| Історія |
|
Незавершені теорії |
|
Науковці |

Спонтанне порушення симетрії — спосіб порушення симетрії фізичної системи, за якого початковий стан та рівняння руху системи інваріантні відносно деяких перетворень симетрії, але в процесі еволюції система переходить у стан, для якого інваріантність відносно деяких (усіх) перетворень початкової симетрії вже є порушеною.
Спонтанне порушення симетрії завжди пов'язане з виродженням стану з мінімальною енергією (вакууму). Множина всіх вакуумів має початкову симетрію, однак кожен вакуум окремо — ні. Наприклад, кулька в двох'ямковому жолобі скочується з нестійкого симетричного стану в стійкий стан із мінімальною енергією або вліво, або вправо, руйнуючи при цьому симетрію відносно зміни лівого на праве (інверсія).
Спонтанне порушення симетрії відбувається (псевдо)випадковим чином і зумовлене флуктуаціями. Це явище надзвичайно поширене в природі. Безліч різноманітних прикладів спонтанного порушення симетрії можна навести з класичної механіки.
Однак, тоді як у механіці спонтанне порушення симетрії має радше описове значення, у теорії поля це є основний принцип, що забезпечує генерацію мас калібрувальних бозонів. Більше того, будуючи ефективні лагранжіани в квантовій теорії поля, можна деякі мезони ототожнити з відповідними голдстоунами (псевдогодстоунами). Нижче розглянуто приклад -мезона як голдстоуна при порушенні деякої симетрії квантової хромодинаміки з безмасовими кварками.
Так само речовину в певній термодинамічній фазі можна розглядати як квантове поле з відповідною симетрією. Тоді спонтанне порушення симетрії представляється як фазовий перехід.
Існування в природі чотирьох фундаментальних взаємодій теж є наслідком порушення симетрії — гіпотетично при досить великих енергіях (~100 ГеВ) електромагнітні й слабкі ядерні сили об'єднуються в одну електрослабку взаємодію, а при ще більших енергіях (~1014 ГеВ) об'єднуються електрослабка і сильна ядерна взаємодії у взаємодію Великого об'єднання.
Механізм спонтанного порушення симетрії життєво необхідний для можливості існування суперсиметрії. Непорушена суперсиметрія передбачає існування у кожної відомої частинки суперпартнера з такою ж самою масою, чого не спостерігається в експериментах. Вважається, що через порушення суперсиметрії суперчастинки набувають великої маси, недосяжної для сучасних експериментів.
Вакууми можуть мати доволі цікаву структуру. Квантова теорія поля дозволяє існування польових вакуумних конфігурацій зі спонтанно порушеними вакуумами, які змінюються від точки до точки. Такими станами є наприклад магнітні монополі, космічні струни, доменні стінки. Стани такого типу спостерігаються у фізиці конденсованого стану, наприклад, стінки між феромагнітними доменами. При складних багатоямних конфігураціях потенціалу існує кілька вакуумів. Однак справжнім вакуумом є лише стан із найменшою енергією. Усі інші вакууми є метастабільними й переходять у справжній шляхом квантового тунелювання.
Спонтанне порушення симетрії може відігравати велику роль і в гравітації. Вважається, що космологічна інфляція спричинена переходом з фальшивого вакууму в істинний при спонтанному порушенні симетрії Великого Об'єднання. Крім того спонтанне порушення суперсиметрії (суперхіггсівський механізм) передбачає теорії масивної гравітації. Також розвиваються моделі гравітаційного поля метричного тензора як хіггс-голдстоунівського поля деякої порушеної симетрії.
Таким чином спонтанне порушення симетрії є надзвичайно поширеним явищем в усіх галузях фізики, починаючи від класичної механіки, закінчуючи квантовою гравітацією.
Прості приклади спонтанного порушення симетрії[ред. | ред. код]
У класичній механіці[ред. | ред. код]
Крісло
Рівняння, які описують рух атомів будь-якого несиметричного фізичного тіла, наприклад, крісла, інваріантні відносно тривимірних поворотів, однак розв'язок цих рівнянь — реальне крісло — має певну орієнтацію в просторі[1].
Скочування кульки у двохямному жолобі
Кулька, що перебуває посередині між ямами двохямного жолоба, рано чи пізно під впливом збурень скотиться в один з них, порушуючи симетрію відносно заміни
Олівець на столі
Олівець, поставлений на торець на столі, не має жодного вибраного напряму в площині стола, однак під дією збурень він упаде, вибравши про цьому якийсь псевдо-випадковий (залежний від флуктуацій) напрям.
Стрижень під пресом
Круглий металевий стрижень, затиснутий між пластинами преса, при достатньому навантаженні зігнеться, причому напрям згину довільний і залежить від флуктуацій. Початкова осьова симетрія стрижня спонтанно порушується.
Розтягнута гумка
Розтягування гумки приводить до її видовження і зменшення в ширині. При певному значенні розтягуючої сили вона рветься в певному місці, хоча для ідеальної гумки всі місця є рівноімовірними. Причиною «порушення» симетрії є флуктуації товщини гумки — рветься, там де тонше. Ідеальна гумка розтягнулася б до ланцюжка з атомів і порвалася б, коли енергія розтягуючої сили стала б рівною сумарній енергії зв'язку атомів
У фізиці конденсованого стану[ред. | ред. код]
Кристалізація[ред. | ред. код]
При кристалізації рідини, яка характеризується найвищою, ізотропною, симетрією, утворюється кристал, у якому існують певні виділені напрямки відносно кристалічних осей. Орієнтація кристалічних осей у загальному випадку випадкова або зумовлена слабкими зовнішніми факторами чи флуктуаціями. Також симетрія відносно трансляцій на довільний вектор понижується до трансляційної симетрії на вектор, який є лінійною комбінацією векторів кристалічної ґратки.
Метастабільні фази[ред. | ред. код]
Рідина при охолодженні нижче температури кристалізації перетворюється на кристал. Однак рідина без домішок може бути охолоджена нижче температури кристалізації. Такий стан досягається завдяки відсутності центрів кристалізації — немає зародків, на яких могли б утворюватися кристали. Утворюється метастабільна фаза переохолодженої рідини.
З точки зору симетрії, ізотропна і трансляційна симетрія рідини мала б знизитися до симетрії кристалічної ґратки, однак нема флуктуацій (центрів кристалізації), які б порушили дану симетрію.
Аналогічна ситуація виникає в пересиченій парі чи перегрітій рідині. Такі метастабільні стани використовуються наприклад в бульбашкових камерах та камерах Вільсона.
Фазові переходи[ред. | ред. код]
Нагріті феромагнетики (вище температури Кюрі) перебувають у парамагнітному стані, де вибраного напряму намагніченості немає, однак охолоджуючись нижче температури Кюрі феромагнетик отримує спонтанну намагніченість (відбувається фазовий перехід), напрям якого (за відсутності зовнішнього магнітного поля) є випадковим і залежить від флуктуацій.
Спонтанне порушення симетрії відбувається майже при всіх фазових переходах (див. нижче).
У квантовій механіці[ред. | ред. код]
Двощілинний експеримент[ред. | ред. код]
При падінні квантової частинки на дві щілини[2], біля кожної з яких розміщений детектор спрацьовує (істинно випадковим чином) один з детекторів. Симетрія випадково порушується. Цей приклад суттєво відрізняється від попередніх тим, що, виходячи з сучасних уявлень (див. Теорема Белла[3], наявність флуктуацій для спонтанного порушення симетрії не є обов'язковою: природа реалізує проходження частинки через одну з можливих щілин абсолютно випадковим чином.
Вимірювання у квантовій механіці[ред. | ред. код]
Прямим узагальненням попереднього прикладу на довільне вимірювання стану в квантовій механіці. У квантовій теорії, згідно з постулатом про вимірювання[3], вимірювання полягає в редукції (миттєвому переході) квантового стану в один з можливих власних станів оператора вимірюваної фізичної величини . Стан при цьому випадковим чином (з ймовірністю ) переходить у стан з порушеною початковою симетрією.
Декогеренція[ред. | ред. код]
Іншим прикладом спонтанного порушення симетрії в квантовій механіці, але вже пов'язаним з наявністю флуктуацій, є декогеренція. Через наявність зовнішніх флуктуацій чистий стан системи переходить в змішаний з порушенням початкових симетрій. Математично це відповідає тому, що декогеренція спричиняє занулення недіагональних елементів матриці густини[3].
Для прикладу, розглянемо квантовомеханчіний атом у збудженому стані. Атом спонтанно випромінює фотон і переходить на нижчий енергетичний рівень. Якщо атом перебуває в сферично симетричному стані, то він випромінює фотон у довільному напрямку і сам перейде в неізотропний стан зі спонтанно порушеною симетрією відносно поворотів. Причиною порушення симетрії є наявність навколишніх частинок, а також випадкові флуктуації фізичного вакууму.
Для ілюстрації декогеренції можна також розглянути ансамбль однакових квантових станів. Через наявність зовнішніх флуктуацій після певного часу системи перебуватимуть в різних станах[3].
Саме знищення недіагональних елементів відповідає за спонтанне порушення симетрії в першому прикладі даного розділу «Крісло»[1].
Спонтанне порушення калібрувальної симетрії[ред. | ред. код]

Порушення глобальної калібрувальної симетрії[ред. | ред. код]
У теорії поля зазвичай розглядають динаміку поля в околі вакуумного стану (мінімуму потенційної енергії), вважаючи самі поля малими. На практиці, це веде до розкладу функції Лагранжа відповідного поля в ряд Тейлора в околі мінімуму потенціальної енергії і нехтування доданками вищих степенів у розкладі. При цьому вибір вакууму може бути неоднозначним (див. Рисунок «Лінійна сигма модель»: сірим кольором показано можливі вакуумні стани).
Наприклад, розглянемо лагранжіан комплексного (зарядженого) поля Клейна — Ґордона[en] де є дійсними полями,
де — потенціал взаємодії, грецькі індекси всюди пробігають значення . Цей лагранжіан є інваріантним відносно глобальних калібрувальних перетворень
де є дійсною константою. Для даної моделі вакуум не є інваріантним відносно таких калібрувальних перетворень, якщо функція має мінімум в точці відмінній від нуля.
Справді, якщо має мінімум в нулі, тоді точці вакууму однозначно відповідає Зовсім інша ситуація виникає у випадку, коли . У цьому випадку мінімуму потенціалу відповідає не одна точка, а континуум точок
Відповідним поворотом системи координат простору зарядових ступенів вільності поля Клейна — Ґордона завжди можна привести вакуум до вигляду
Легко бачити, що хоча лагранжіан (зокрема, наближений) є інваріантним відносно калібрувальних перетворень, вакуум таким вже не є. Система переходить у випадково вибраний (насправді залежно від флуктуацій) стан. У цьому і полягає спонтанне порушення глобальної калібрувальної симетрії.
Розглянемо найпростіший приклад спонтанного порушення симетрії для дійсного поля Клейна — Ґордона, яке задається лагранжіаном
де , . Цей лагранжіан є інваріантним відносно заміни . Поле в цьому випадку має два вакууми, що відповідає наявності в потенційної енергії двох мінімумів при . Але жоден з вакуумів не є інваріантним відносно початкової симетрії інверсії знаку поля. В цьому й полягає спонтанне порушення симетрії (зверніть увагу, що інверсія не є калібрувальним перетворенням).
Внаслідок симетрії лагранжіана відносно інверсії знаку поля, можна обрати будь-який знак вакууму. Не зменшуючи загальності можна обрати "+". Розклавши поле в околі вакуумного стану і вважаючи малою величиною, лагранжіан можна записати
де .
У цьому прикладі необхідно зауважити ще одну важливу деталь. Лагранжіан описує безмасове поле з потенціалом взаємодії . Безмасовим поле є тому, що знак збігається зі знаком кінетичної енергії, а тому не може відповідати за масу. Однак вже лагранжіан описує вільне поле Клейна — Ґордона з масою . Таким чином спонтанне порушення симетрії може генерувати масу поля. Далі це явище буде досліджено більш детально.
Нагадаємо, що калібрувальні перетворення утворюють групу Лі, причому компактну. Розглянемо лагранжіан
де — скалярних дійсних полів. Нехай лагранжіан інваріантний відносно перетворень калібрувальної групи
Випадок інваріантного вакууму[ред. | ред. код]
Якщо має мінімум у точці , то легко бачити, що вакуум є інваріантним відносно всіх калібрувальних перетворень (дія будь-якої матриці на нульовий вектор дає знову нульовий вектор). У такому випадку можна розкласти в ряд Тейлора в околі нуля. Припускаючи, що , а також враховуючи, що перші похідні в точці екстремуму дорівнюють нулю, а матриця других похідних в точці мінімуму є додатно визначеною, отримаємо
Здійснюючи відповідне ортогональне перетворення можна масову матрицю привести до діагонального вигляду. Таким чином отриманий лагранжіан описуватиме дійсних скалярних полів з масами, які визначаються власними значеннями матриці .
Випадок неінваріантного вакууму.[ред. | ред. код]
Зовсім іншою є ситуація, коли потенціал має мінімум не в нулі. В такому випадку завжди існує довільність у виборі вакуумного стану. Вакуум буде інваріантний лише відносно певної підгрупи калібрувальної групи . Групу називають малою групою. Відбувається порушення локальної симетрії калібрувальної групи . Розглянемо приклад порушення глобальної симетрії, що задається калібрувальною групою тривимірних поворотів (SO(3)), в лінійній сигма-моделі[4].
Розглянемо лагранжіан
де присутні три дісних скалярних поля . Лагранжіан такого вигляду називають лінійною сигма-моделлю. Ця модель є інваріантною відносно перетворень групи (ортогональні матриці з одиничним визначником). На вектор елементи групи діють як матриці тривимірних поворотів. Вакуум цього поля вироджений і лежить на точці сфери
Відповідними перетвореннями системи координат завжди можна добитися вибору вакууму у вигляді
Очевидно, що вакуум не є інваріантним відносно , проте він є інваріантним відносно групи поворотів навколо осі .
Розкладемо поле в околі вакууму , вважаючи малою величиною. Лагранжіан при цьому перепишеться
що відповідає двом безмасовим скалярним полям , та полю з масою .
Як бачимо порушення глобальної калібрувальної симетрії може генерувати масу поля.
Загалом можна показати, що має місце
Теорема Голдстоуна[5][6]. При спонтанному порушенні глобальної калібрувальної симетрії виникають безмасових скалярних полів та масивних скалярних полів . Тут є вимірністю вибраного представлення (фактично початкова кількість дійсних скалярних полів).
При цьому безмасові поля, які виникають при спонтанному порушенні глобальної калібрувальної симетрії називаються бозонами Голдстоуна. Ще раз підкреслимо, що їх кількість дорівнює кількості порушених симетрій.
Розглянемо, як і в попередньому прикладі, лагранжіан
де присутні вже дійсних скалярних поля . Така модель є інваріантною відносно перетворень групи .
При порушенні симетрії вакуум буде інваріантний відносно групи . Вимірність групи рівна . Тоді число бозонів Голдстоуна, які утворюються при стонтанному порушенні локальної симетрії рівне .
Отже, при спонтанному порушенні глобальної симетрії виникають бозонів Голдстоуна та один масивний бозон.
У випадку за теоремою Голдстоуна отримуємо 2 голдстоунівські бозони і одне масивне поле, що було безпосередньо перевірено в попередньому прикладі.
Доведення теореми Голдстоуна[ред. | ред. код]
Позначимо генератори малої групи як для фундаментального представлення групи чи для будь-якого іншого представлення. Тоді з умови інваріантності вакууму випливає, що . Розкладаючи експоненту в ряд, отримаємо, що дія генераторів малої (непорушеної) групи на вакуум знищує вакуум
- .
Ця умова є важливим критерієм непорушеної симетрії.
Решту генераторів групи позначимо як (чи ). Їх дія на вакуум не дає нуль, інакше б перетворення, згенеровані ними, залишали б вакуум інваріантним і належали малій групі. Можна ввести вектори . Їх є , вони лінійно незалежні та утворюють базис в підпросторі голдстоунівських бозонів (порушених симетрій).
В усьому просторі зручно ввести ортонормований базис , де вектори є ортами голдстоунівського підпростору і складені з лінійних комбінацій векторів , а векторів утворюють базис решти простору. Тоді скалярні поля можна розкласти в такому базисі
а лагранжіан в квадратичному наближенні має вигляд
з якого явно не видно виконання теореми Голдстоуна. Однак з умови калібрувальної інваріантності мінімуму потенціалу (не плутати з вакуумом, мова йде про інваріантність значення потенціалу і його похідних)
Для непорушеної симетрії і ця рівність очевидна, однак для порушених симетрій , а враховуючи, що з лінійних комбінацій отримуємо базис випливає А тому лагранжіан перепишеться у вигляді
де . Такі міркування власне доводять теорему Голдстоуна. Фактично це є розгляд спонтанного порушення симетрії в загальному випадку, який однак можна легко провести у випадку конкретної симетрії як у прикладах.
Порушення локальної калібрувальної симетрії[ред. | ред. код]
Розглянута вище теорема Голдстоуна[5][6] стверджує, що при порушенні калібрувальної симетрії виникають безмасові безспінові бозони. Через відсутність таких частинок у природі, теорема Голдстоуна розглядалася як контраргумент проти порушених симетрій. Однак, як виявилося, коли порушується локальна, а не глобальна калібрувальна симетрія, то безмасові голдстоуни відсутні, а натомість калібрувальні векторні поля отримують масу[7][8]. Спонтанне порушення локальної калібрувальної симетрії є важливим явищем в теорії поля, оскільки воно веде до набуття калібрувальними полями мас (нагадаємо, що самі по собі масові доданки для калібрувального поля не є калібрувально інваріантними, тому в лагранжіані поля з непорушеною симетрією вони відсутні). Такий механізм носить назву механізму генерації мас Хіггса.
Локальні перетворення відрізняються від глобальних наявністю координатної залежності . Така залежність приводить до виникнення в лагранжіані калібрувальних полів (у випадку зарядженого поля Клейна — Ґордона — електромагнітного поля з групою симетрії , при розгляді трикомпонентного вектора скалярних полів з групою симетрії — калібрувального поля, яке можна ототожнити з колірним глюонним полем сильної ядерної взаємодії, тощо).
Розглянемо лагранжіан
де — набір скалярних полів, — тензор відповідного калібрувального поля, — коваріантна похідна (векторний потенціал в загальному є матрицею, яка діє на векторний стовпець , індекс пробігає значення від 1 до і нумерує компоненту розкладу потенціалу по генераторах групи симетрії. Цей лагранжіан є інваріантним відносно локальних калібрувальних перетворень що утворюють групу . Поля при калібрувальних перетвореннях перетворюються наступним чином
Випадок інваріантного вакууму.[ред. | ред. код]
Якщо мінімум реалізовується при , то в такому випадку можна розкласти лагранжіан в ряд Тейлора в околі вакууму і отримати в квадратичному наближенні лагранжіан
який описує масивних скалярних полів, та безмасових калібрувальних векторних полів .
Обчислимо число польових ступенів вільності набору цих полів. Оскільки скалярне поле має одну ступінь вільності, а безмасове векторне поле — дві, то сумарна кількість ступенів вільності рівна .
Випадок неінваріантного вакууму.[ред. | ред. код]
Основна відмінність локальної калібрувальної симетрії від глобальної полягає в залежності калібрувальної константи від координат . Ця координатна залежність дозволяє відповідним вибором занулити поля всіх безмасових голдстоунівських бозонів в усьому просторі. Таке калібрування називається унітарним (можна показати, що воно зажди існує у випадку компактних калібрувальних груп[9]). Однак це калібрування приводить до появи в лагранжіані масових доданків типу , які тим не менше є калібрувально інваріантними. При унітарному калібруванні масові доданки виникають рівно для калібрувальних полів. Оскільки унітарним калібруванням знищуються бозони Голдстоуна, а виникають масивні калібрувальні бозони, то часто кажуть, що векторні поля «з'їдають» голдстоуни і набувають маси. Умова унітарного калібрування може бути записана через «матричні елементи» генераторів порушеної симетрії у вигляді
Ця формула означає, що поле ортогональне до всіх векторів простору порушених симетрій.
Також при спонтанному порушенні симетрії виникають масивних скалярних поля, які називаються бозонами Хіггса. Кількість полів, які отримуються в результаті спонтанного порушення локальної калібрувальної симетрії визначається з
Теорема Хіггса[7]. При спонтанному порушенні локальної калібрувальної симетрії присутні масивних скалярних полів (бозонів Хіггса), безмасових векторних полів, а також масивних векторних полів (кількість масивних калібрувальних бозонів дорівнює кількості порушених симетрій).
Знайдемо кількість польових змінних в такій системі. Враховуючи, що масивне поле має три ступені вільності, сумарна кількість польових ступенів вільності дорівнює , що збігається з результатом для інваріантного вакууму.
Розглянемо лагранжіан
де індекс пробігає значення від 1 до 3. Вакуумний стан можна вибрати у вигляді . Як і в попередніх прикладах розкладемо польові функції в околі вакууму . В квадратичному наближенні по полю лагранжіан перепишеться
Діагоналізуємо отриманий лагранжіан за допомогою заміни
Діагоналізований лагранжіан має вигляд
Як бачимо, отриманий внаслідок спонтанного порушення симетрії лагранжіан описує одне скалярне поле з масою , одне безмасове векторне поле , та два масивні векторні поля з масами , що є у повній відповідності з загальними міркуваннями, наведеними вище.
Варто зазначити, що унітарне калібрування залишає певну симетрію в лагранжіані. Групою цієї симетрії є мала група . У випадку порушення симетрії (приклад вище) малою групою є група поворотів відносно осі . Зауважимо, що група ізоморфна групі калібрувальної симетрії електромагнітного поля.
Доведення теореми Хіггса[ред. | ред. код]
Для доведення теореми Хіггса як і у доведенні теореми Голдстоуна розкладемо скалярне поле , крім цього розкладемо калібрувальне поле за генераторами калібрувальної групи : .
У квадратичному наближенні розклад для скалярних полів буде мати такий самий вигляд як і у доведенні теореми Голдстоуна, квадрат тензора поля , а коваріантна похідна в першому наближенні (лінійного наближення за відхиленнями від вакууму достатньо для отримання квадратичного по відхиленню лагранжіана) запишеться у вигляді
Підстановка даних виразів у вихідний лагранжіан дає у квадратичному по полях наближенні лагранжіан
де . Зауважимо, що матриця є невиродженою, оскільки фактично є матрицею переходу між базисами .
Можна ввести поля (це відповідає унітарному калібруванню), тоді остаточно лагранжіан запишемо у вигляді
де , . Звідси одразу ж отримується формулювання теореми Хіггса.
Спонтанне порушення наближеної симетрії[ред. | ред. код]
В попередніх підрозділах розглядалася ситуація, коли вихідний лагранжіан володіє певною симетрією групи , яка спонтанно порушується. Зараз розглянемо випадок, коли до лагранжіана зі симетрією додаються малі доданки, які руйнують симетрію (інколи наявність малих несиметричних доданків на відміну від спонтанного порушення симетрії називається м'яким порушенням симетрії). При спонтанному порушенні наближеної симетрії виникають безспінові поля малої маси, які називають псевдоголдстоунівськими бозонами[10].
Нехай потенціальна енергія записується у вигляді , де доданок задовольняє умову інваріантності відносно перетворень групи : , являє собою збурення, яке руйнує симетрію, — малий параметр. Доданок зміщує вакуумний стан в точку . Тоді умова мінімуму запишеться
Якщо помножити останнє рівняння на , та враховуючи, що другий доданок дасть (умова інваріантності значення вакууму відносно перетворень калібрувальної групи, див. Доведення теореми Голдстоуна), отримуємо
Отримане рівняння має назву умови підлаштування вакууму[11]. Якщо ця умова не задовольняється, то навіть мале збурення приводить до настільки великих змін , що члени розкладу в околі не є малими поправками. Однак у випадку, коли є компактною групою Лі, ця умова виконується[1]. По аналогії до розкладу в пункті «Доведення теореми Голдстоуна» можна отримати масову матрицю псевдоголдстоунівських бозонів
Масова матриця псевдоголдстоунівських бозонів є додатно-визначеною[1][10].
Порушення симетрії квантового поля[ред. | ред. код]
У квантовій теорії польова змінна перестає бути просто дійсною чи комплексною функцією координат, а є лінійним оператором у гільбертовому просторі станів поля, які в представленні Фока мають вигляд[12][4][13].
де — стала нормування, є так званим оператором породження, який збільшує число частинок з певним імпульсом на 1, наприклад для бозонів , — вакуумний стан, в якому нема жодних частинок (збуджень). Спостережуваними величинами є середні від польових операторів на станах поля , де — деякий оператор, поліноміальний по операторах поля.
Однак можна показати, що середнє оператора на станах можна переписати через вакуумне середнє від оператора , який є теж поліноміальним по операторах поля. Такі вакуумні середні зручно обчислювати як функціональні похідні від так званого твірного функціоналу, який означається як функціональний інтеграл[en]
де — класична дія полів .[4][13] Твірний функціонал являє собою амплітуду переходу вакуум-вакуум.
Найчастіше твірний функціонал та його похідні обчислюють, проводячи розклади в околі дії вільних невзаємодіючих полів (квадратичних по полях лагранжіанів). Поправки до невзаємодіючої теорії зручно обчислювати за допомогою діаграм Фейнмана.
Так як і в квантовій механіці по відношенню до класичної, операторна природа поля приводить до нетривіальних квантових ефектів. Інколи квантові поправки є незначними, однак в загальному вони можуть мати значний (потенційно нескінченний) вклад. Часто для квантового поля мають місце квантові аномалії — порушення симетрійних характеристик квантової системи, які є в класичного відповідника. Тому викладена в попередньому розділі фізична картина порушення симетрії для класичного поля не може бути безпосередньо екстрапольована на квантовий випадок і апріорі стверджувати виконання теорем Голдстоуна чи Хіггса у квантовому випадку не можна.
Глобальна калібрувальна симетрія[ред. | ред. код]
Теорема Голдстоуна у квантовому випадку може бути легко показана в формалізмі ефективної дії[en] (потенціалу). В рамках цього підходу вводяться додаткові класичні струми , які взаємодіють з скалярними полями . Твірний функціонал може бути переписаний у вигляді
де величина являє собою суму всіх зв'язних вакуумних діаграм (діаграми, які утворюються одна з одної перестановкою вершин різними не вважаються). Вакуумні середні значення польових операторів при заданих класичних струмах переписуються через варіаційні похідні від
Означимо як струм, для якого вакуумне польове середнє рівне наперед заданому полю . Здійснивши перетворення Лежандра від отримаємо квантову ефективну дію [14]
Величина є сумою всіх зв'язаних одночастинково незвідних діаграм при наявності струму . Можна показати, що
При відсутності зовнішніх струмів , значення вакуумних середніх визначаються як стаціонарні точки функціоналу
Ефективна дія враховує квантові поправки всіх порядків, при цьому забезпечуючи класичне трактування поля вакуумних середніх польових операторів. Якщо прийняти, що вакуум є інваріантним відносно перетворень Лоренца трансляцій і поворотів, то можна показати, що ефективна дія записується у вигляді
де — об'єм простору-часу, а — звичайна функція, яка називається ефективним потенціалом[1].
Згідно з тотожностями Славнова — Тейлора[15][16] ефективна дія інваріантна відносно інфінітезимальних перетворень вакуумних полів (тут під мається на увазі будь-яке поле, а не тільки скалярні). Для широкого класу так званих лінійних інфінітезимальних перетворень (до яких відносяться і калібрувальні перетворення)
де — постійна матриця, ефективна дія інваріантна відносно тих самих симетрій, що і вихідна класична дія[1]. Таким чином, якщо така симетрія непорушена на класичному рівні, то вона не буде порушена квантовими поправками у будь-якому порядку теорії збурень.
За допомогою ефективного потенціалу доведення теореми Голдстоуна в квантовому випадку можна провести майже такими самими міркуваннями як і для класичних полів (з точністю до заміни потенціалу на ефективний потенціал і класичних полів на вакуумні середні польових операторів). В квантовій теорії поля значення квадратів мас бозонів після порушення симетрії визначаються власними значеннями масової матриці . А оскільки, як було сказано вище, симетрія ефективної дії (потенціалу) відносно калібрувальних перетворень така сама як і вихідної дії, то кількість нульових власних значень квантової масової матриці така сама як і для класичної, а теорема Голдстоуна виконується і у квантовому випадку.
Локальна калібрувальна симетрія[ред. | ред. код]
У квантовій теорії поля, теорема Хіггса залишається справедливою, хоча через причини наведені на початку розділу, математичний розгляд проблеми є складнішим. Для видалення «нефізичних» голдстоунівських мод при розгляді порушення локальної калібрувальної симетрії класичного поля використовувалося унітарне калібрування. Однак при застосуванні унітарного калібрування в квантовій теорії поля виявляється, що пропагатор калібрувального поля має асимптотичну поведінку , а тому просто перевірити теорію на перенормовність (підрахунком степенів) не вдається. В квантовій теорії поля використовується залежне від дійсного параметра так зване -калібрування, яке є узагальненням унітарного калібрування[17][18][19]. Перевагою сімейства таких калібрувань є асимптотика пропагатора калібрувального поля.
Так чи інакше, вибір калібрування накладає додаткові умови на польові змінні, які потрібно враховувати при квантуванні. В теорії поля такі умови враховуються в рамках методу Фаддеєва — Попова[20]. Розглянемо лагранжіан
Розкладаючи скалярні поля в околі мінімуму , можна переписати лагранжіан як функцію : . При цьому калібрування фіксується умовою , матриця була введена в попередньому розділі при розгляді доведенні теореми Хіггса у класичному випадку. Всього таких умов є . Введемо функції , які будуть враховувати калібрування. При -калібрування переходить в калібрування Ландау . Унітарне калібрування отримується в границі .
Квантування теорії ведеться за допомогою твірного функціонала
де — калібрувальні параметри порушених симетрій. Остаточно квадратичний по полях лагранжіан записується у вигляді
де , , .
Визначник під інтегралом можна врахувати, додавши до лагранжіану системи лагранжіан духів Фаддєєва — Попова :.
Наявність мас у голдстоунів (які однак пропорційні ) та -залежність мас бозонів Хіггса залежать від калібрування, що означає їхню нефізичність. Якщо їх не брати до уваги, то отримані масові матриці показують повну відповідність квантової з класичною теоремами Хіггса. Однак самі значення мас можуть дещо змінюватися внаслідок квантових поправок.
Пі-мезони як псевдоголдстоуни[ред. | ред. код]
Як приклад порушення симетрії у квантовій теорії поля розглянемо порушення кіральної симетрії квантової хромодинаміки з безмасовими кварками. Ферміонний лагранжіан безмасових кварків має вигляд
де риска над полем означає діраківське спряження , спінори відповідають -кваркам. Взагалі кажучи, спінори кварків утворюють колірні триплети, проте цього явно виписувати тут не будемо. Такий безмасовий лагранжіан інваріантний відносно перетворень групи ізоспінового дублету
де , а — матриці Паулі. Даній симетрії відповідають векторний і аксіальний струми симетрії
з рівнянням неперервності , де позначає ізоспіновий кварковий дублет. Відповідні заряди симетрії є генераторами ізоспінової та залишкової симетрій. Діючи на кваркові поля, ці оператори індукують перетворення
- .
Якщо симетрія є непорушеною, то кожному гадрону відповідає аналог з тими самими квантовими числами (спіном, баріонним зарядом), але з протилежною парністю. Однак виродження гадронного спектру по парності не спостерігається, тому слід припустити, що кіральна симетрія з генераторами є порушеною.
Слід однак зауважити, що через наявність в лагранжіані масових доданків симетрія є наближеною. Тому, як було показано в попередньому розділі, в спектрі частинок виникають псевдоголдстоунівські бозони з малою масою. Вони повинні бути безспіновими, мати нульовий баріонний заряд, з ізоспіном рівним 1 та від'ємною парністю. Найлегшими серед всіх гадронів є саме -мезони, більше того вони володіють необхідними квантовими числами. Можна показати[1], що квадрат масової матриці -мезонів і дає масу -мезона 140 МеВ при 10 МеВ, що відповідає реальності.
Поле Хіггса і динамічне порушення симетрії[ред. | ред. код]
Динамічне порушення симетрії[21][22][23] полягає в порушенні симетрії квантовими ефектами поляризації вакууму. Такі поляризаційна ефекти порушують початкову класичну калібрувальну симетрію групи , редукуючи її до симетрії з малою групою . Поляризація вакууму може приводити до набуття початково безмасовими частинками мас[24].
У такій ідеології бозон Хіггса може бути введений в теорію наступним чином[25]. Нехай маємо систему матеріальних і калібрувальних полів, які позначимо для зручності одною буквою . Нехай відповідна дія інваріантна відносно перетворень калібрувальної групи . Введемо в систему класичне зовнішнє поле Хіггса , яке редукує калібрувальну симетрію до малої групи , дію такої системи запишемо . Твірний функціонал запишемо у наступному вигляді з інтегруванням тільки за полями , вважаючи поле заданим
Тепер до дії додамо «затравочну» дію для Хіггсового поля , а в твірному функціоналі додамо інтегрування за полями
Інтегрування за полями генерує деяку ефективну дію для поля Хіггса
Перевагою такого підходу є отримання нетривіального вкладу в Хіггсове поле, яке походить від початкової системи полів . Аналогічними методами в квантовій електродинаміці отримують нелінійні поправки до лагранжіану[26].
Порушення симетрії у статистичній фізиці[ред. | ред. код]
Різні статистичні системи можна представляти як деякі квантовані поля, так система бозе-частинок (наприклад ) являє собою комплексне скалярне поле, фермі-система () представляється як спінорне поле, проте найчастіше в квантовій статистичній фізиці лагранжіани є ефективними феноменологічними, а відповідні поля описують певні збудження в системі (теорія Гінзбурга — Ландау[27], плазмони, фонони, екситони тощо).
Математичний апарат квантової теорії поля може бути застосований до вивчення статистичних систем багатьох частинок. При цьому в статистичній фізиці терміни квантової теорії полі мають свої відповідники. Так, наприклад, аналогом твірного функціоналу є статистична сума, яка може бути представлена як функціональний інтеграл
де — вільна енергія Гельмгольца, яка є аналогом класичної дії у квантовій теорії поля, — сукупність полів моделі, — обернена температура, — густина енергії в околі точки , — хімічний потенціал.
Зрозуміло, що і як у випадку квантової теорії поля, при квантуванні статистичної системи виникають квантові поправки, які можуть мати який завгодно вплив на систему. Однак по аналогії до попереднього розділу можна ввести ефективний потенціал, який зручно використовувати для дослідження системи. Проте, якщо цього достатньо, можна працювати в наближенні середнього поля, в рамках якого покладається[28]
Фазові переходи як спонтанне порушення симетрії[ред. | ред. код]
При зміні температури змінюється і густина енергії системи (через зміну потенціалу взаємодії) і хімічний потенціал, тому може статися, що при температурах вище певної критичної температури мінімум енергії знаходиться при одній конфігурації системи, а нижче — при іншій (чи навпаки). Система переходить з стану, який вже не є стабільним при даній температурі, в новий стабільний стан. Макроскопічно спостерігається фазовий перехід.
Поля відхилення від вакуумного стану ототожнюють з термодинамічними флуктуаціями. При спонтанному порушенні симетрії в статистичній фізиці, крім масивних скалярів, завжди виникають безмасові моди флуктуацій, які називають бозонами Голдстоуна (часто Намбу — Голдстоуна). Наявність безмасових голдстоунівських мод веде до безщілинного енергетичного спектру системи (теорема Гугенгольца — Пайнса[29]). Голдстоунівська мода також відповідає за скорельовані в усій системі флуктуації (так званий недіагональний дальній порядок, наприклад у випадку бозе-суміші — бозе-конденсат). Інколи необґрунтовано у фізиці конденсованого стану масивні моди коливань називають бозонами Хіггса.
Майже всі фазові переходи можна трактувати як спонтанне порушення симетрії. Тим не менше існують стани речовини, які не можна представити як спонтанно порушені конфігурації поля. До таких станів, відносять спінові рідини, електронний газ в дробовому квантовому ефекті Холла[30].
Надплинність[ред. | ред. код]
Як приклад спонтанного порушення симетрії в теорії фазових переходів розглянемо перехід рідкого в надплинний стан. Як було сказано раніше, бозе-рідину можна описати одним комплексним полем .
У теорії надплинної бозе-рідини, припускаючи, що атоми рідини є твердими кульками, які взаємодіють лише при безпосередніх зіткненнях (-відштовхування), а далекодіючі взаємодії відсутні, густину енергії можна записати у вигляді[31]
де — комплексне поле, що відповідає хвильовій функція атомів рідини, — маса атомів рідини, — параметр взаємодії. Хімічний потенціал має вигляд . Даний вираз для густини енергії відповідає лагранжіану Гінзбурга — Ландау[27] без зовнішнього магнітного поля. Вперше квантовопольовий розгляд надплинності провів Пітаєвський[32].
При температурах вище критичної енергія має мінімум при . Однак при пониженні температури нижче критичної мінімум реалізовується при . Основний стан стає безмежнократно виродженим по відношенню до фази .
Питома вільна енергія (на одиницю об'єму) вище критичної температури рівна нулю , проте нижче критичної температури (безвідносно до значення фази) , де .
Теплоємність одиниці об'єму Така поведінка теплоємності відповідає фазовому переходу другого роду.
Розкладаючи поля та в околі вакууму отримаємо
де безрозмірні величини мають вигляд , . Відхилення від вакуумних (рівноважних) значень відповідають полям збуджень (флуктуацій). Як бачимо існують дві моди коливань — масивна мода та безмасова голдстоунівська мода .
Моди коливань характеризуються кореляційною довжиною . Вона задає експоненційний закон загасання збуджень з відстанню . Вище критичної точки є дві моди з кореляційною довжиною . Нижче критичної точки для голдстоунівських безмасових мод кореляційна довжина нескінченна (це означає насправді не експоненційну, а степеневу поведінку збуджень), що відповідає скорельованості фазових флуктуацій в усій системі (наприклад бозе-конденсат). Для масивної моди в надплинному стані маємо температурну залежність кореляційної довжини в околі критичної точки фазового переходу
- .
Об'єднання фундаментальних взаємодій[ред. | ред. код]
Модель Глешоу — Вайнберга — Салама[ред. | ред. код]
Модель Глешоу — Вайнберга — Салама[33][34][35] описує об'єднану електрослабку взаємодію з групою калібрувальної симетрії та чотирма калібрувальними векторними бозонами , де індекс вгорі вказує електричний заряд бозона. При пониженні енергії група порушується до групи електродинаміки з одним калібрувальним бозоном — фотоном. Зауважимо, що непорушена група є групою поля гіперзаряду, а не електромагнітного поля. Також в теорії є скалярне поле, яке перетворюється по фундаментальному представлення групи, тому воно має вигляд двокомпонентного комплексного скаляра . Крім того в моделі є матеріальні поля, які ми для простоти брати до уваги не будемо. Лагранжіан калібрувальних полів (точніше бозонного сектору) має вигляд
де коваріантна похідна від записується
де і — константи взаємодії для відповідних полів, — сукупність одиничної матриці і матриць Паулі .
Вакуумний стан оберемо у вигляді . Очевидно, що вакуум є інваріантний відносно дії елементів малої групи , генератором якої є матриця . Саме ця група відповідає калібрувальним перетворенням електродинаміки. Зручно ввести трійку матриць , а також переписати параметри і через нові параметри та
параметр виявляється рівним елементарному електричному заряду, а параметр називається кутом Вайнберга. В такому випадку коваріантна похідна запишеться
де , , .
В унітарному калібруванні , де є дійсним скалярним полем, що відповідає бозону Хіггса, знайденим експериментально у 2012 році.
В квадратичному наближенні лагранжіан з порушеною симетрією запишеться
де , , .
Насамкінець слід додати, що квантові поправки приводять до зміни мас бозонів та залежності констант взаємодії від енергії.
SU(5)-модель Великого об'єднання Джорджі — Глешоу[ред. | ред. код]

При високих енергіях (~1014 ГеВ) електрослабка і сильна ядерні взаємодії об'єднуються в єдине поле з деякою калібрувальною групою симетрії, яка спонтанно порушується до групи Стандартної моделі при нижчих енергіях. В даному параграфі розглянемо модель Джорджі — Глешоу[en][36] з найменшою калібрувальною групою , яка дозволяє Велике об'єднання.
У цій теорії всі ферміони об'єднуються в три покоління 15-ти компонентних мультиплетів, які складаються з 5-ти і 10-ти компонентних мультиплетів, що відповідає найменшим вимірностям незвідних представлень групи . В 5-компонентний сектор 15-ти компонентного мультиплета входить правий кольоровий триплет кварків -типу (по одній компоненті для кожного кольору) та лівий лептонний ізоспіновий дублет (електрон і нейтрино) . 10-компонентний сектор містить лівий і правий триплети -кварків, лівий триплет -кварків та правий електрон .
При точній симетрії група має безмасові калібрувальні бозони. Існують три бозони , що відповідають за переходи в лептонному квінтеті і пов'язані групою . Також є бозон , що відповідає групі . Як і в Стандартній Моделі, фотон і бозон є ортогональними суперпозиціями полів і . Також є 8 глюонів, що здійснюють переходи між трьома кольоровими кварками та є генераторами групи . Дванадцятьма іншими калібрувальними бозонами є чотири кольорові триплети та . Бозони та відповідають за взаємодії , , та , , відповідно.
При зменшенні енергії симетрія порушується до . При цьому калібрувальні - та -бозони набувають маси 1014 ГеВ.
Крім того, в моделі можливе введення масивних правих нейтрино (як синглет ). Таке нейтрино може взаємодіяти з квінтетом за допомогою бозонів Хіггса, які виникають при спонтанному порушенні симетрії Великого об'єднання.
Модель Джорджі — Глешоу передбачає час життя протона ~1029 років, однак сучасні експерименти на Super-Kamiokande дають нижню оцінку для життя протона 1032 років, повністю виключаючи можливість реалізації симетрії в такій найпростішій версії.
SO(10)-модель та моделі з вищими калібрувальними групами[ред. | ред. код]
Наступною мінімальною калібрувальною групою, якою можна описати Велике об'єднання, є група [37], в якій ферміони утворюють 16-плет (у порівнянні з додається ліве нейтрино). Легко обчислити, що всього є калібрувальних бозонів, які можуть набувати масу при спонтанному порушенні симетрії . Така модель теж виключається відсутністю розпаду протона.
Розглядаються й вищі групи та (наприклад , тощо). Крім того розглядаються моделі, де калібрувальна група є добутком двох і більше простих груп [38], тощо. Особлива увага приділяється ланцюжку виключних груп
які виникають у теоріях багатовимірної гравітації і теорії струн. Групи є достатньо великими для вміщення різних поколінь частинок.
Незважаючи на велику кількість полів у високих групах, механізм спонтанного порушення симетрії у відповідних теоріях такий самий, як і описано вище.
Спонтанне порушення суперсиметрії[ред. | ред. код]
Спонтанне порушення суперсиметрії (на відміну від м'якого та динамічного) полягає в отриманні несуперсиметричної (явно) теорії в околі вакууму з суперсиметричної. Порушення суперсиметрії є необхідним процесом для уникнення конфлікту суперсиметричних моделей з експериментом. Справа в тому, що точна суперсиметрія передбачає, що суперпартнери (кількість яких збігається з кількістю звичайних частинок) мають таку саму масу, як і їх партнери (звичайні частинки), чого не спостерігається в експерименті. Під час порушення суперсиметрії, суперпартнери набувають значної додаткової маси, і, таким чином, стають поки недосяжними в експериментах.
Як і для порушення калібрувальної симетрії, можна показати, що квантові поправки не порушують суперсиметрії, якщо вона не порушена на класичному рівні[39]. Однак суттєвою відмінністю порушення суперсиметрії від калібрувальної симетрії є твердження наступної теореми
Теорема[39]. У будь-якій теорії з суперсиметрією або порушені всі суперсиметрії, або не порушена жодна з них.
Критерії порушеної суперсиметрії[ред. | ред. код]
Ненульові вакуумні середні
Суперсиметрія порушена тоді і тільки тоді, коли суперзаряд не знищує вакуумний стан . Для вакуумного середнього варіації поля можна написати , таким чином суперсиметрія порушена тоді і тільки тоді, коли вакуумне середнє деякого поля не рівне 0. При цьому вимагається Лоренц-інваріантність вакууму.
Наприклад для моделі Весса — Цуміно[40]
з бозонними полями та майоранівським ферміоном . Поля є додатковими і занулюються на масовій поверхні, їхня наявність є необхідною для рівності бозонних і ферміонних ступенів вільності на і поза межами масової поверхні Для цієї моделі з вимоги Лоренц-інваріантності вакууму випливає , , . Ненульове середнє варіації поля має вигляд . Таким чином суперсиметрія порушена тоді і тільки тоді, коли вакуумні середні додаткових полів не рівні 0.
Нульове значення потенціалу
Гамільтоніан суперсиметричної теорії з суперзарядами записується у вигляді
А це в свою чергу приводить до наступного твердження: суперсиметричний вакуумний стан повинен мати нульову енергію, якщо вакуумна енергія додатна — суперсиметрія порушена. Справді, для вакуумного середнього гамільтоніана

Причому рівність досягається тільки у випадку непорушеної суперсиметрії .
В цьому полягає принципова відмінність спонтанного порушення суперсиметрії від калібрувальної симетрії. Для останньої важливо інваріантність мінімуму потенціалу, а для суперсиметрії — значення його мінімуму. Таким чином порушення калібрувальної симетрії є в певному сенсі незалежним від порушення суперсиметрії. Якщо мінімум порушеного відносно калібрувальної симетрії вакууму має нульову енергію, то суперсиметрія не є порушеною.
Голдстіно і хіггсіно[ред. | ред. код]
При порушенні суперсиметрії кірального суперполя де , — грасманові координати суперпростору, реалізовується так зване порушення суперсиметрії -типу, коли вакуумне середнє динамічного скалярного і додаткового поля . При порушенні суперсиметрії векторного суперполя , а відповідне порушення суперсиметрії є -типу.
В обох типах порушення суперсиметрії існує спінор, який під дією суперсиметричних перетворень отримує неоднорідний член
Такий спінор називають ферміоном Голдстоуна або голдстіно.
За аналогією з механізмом Хіггса, де векторний бозон «з'їдає» голдстоун і стає масивним, в супергравітації гравітіно з'їдає голдстіно (векторний супермультиплет з'їдає кіральний) і стає масивним. Такий механізм називається суперхіггсівським механізмом[41][42].
Модель О'Рейферті[ред. | ред. код]
Розлянемо порушення суперсиметрії на прикладі моделі О'Рейферті[43] з кіральними супермультиплетами , яка задається лагранжіаном
де риска над полем означає діраківське (або комплексне) спряження, позначає ермітово спряжений доданок, а суперпотенціал
- .
Варіюючи дію отримуємо рівняння для додаткового поля . Підставляючи отриманий розв'язок отримаємо потенціальну енергію
Суперсиметрія в даній моделі порушена якщо неможливо знайти такий набір , щоб для всіх компонент.
Неінваріантні вакууми[ред. | ред. код]
При розгляді порушення симетрії квантового поля ми припускали, що вакуумна конфігурація поля є інваріантною відносно перетворень неоднорідної групи Лоренца (повороти, бусти і трансляції). Це дуже сильне неаргументоване обмеження на вакуумні конфігурації, яке веде до того, що вакуум поля є однаковий у всіх точках простору. Однак виявляється, що справді є можливими нетривіальні координатно-залежні конфігурації вакууму поля. Більше того, такі конфігурації можуть бути важливими при обчисленні твірного функціоналу, оскільки їхній вплив не є малою величиною (наприклад інстантонний[44] внесок у квантову хромодинаміку). Такими нетривіальними вакуумами також є магнітні монополі[45][46], космічні струни[47] та доменні стінки[48], які в принципі можуть бути присутніми у Всесвіті і трактуються як топологічні дефекти простору-часу з непорушеною калібрувальною електрослабкою симетрією чи симетрією Великого об'єднання. Такі неінваріантні вакуумні стани реалізують екстремум функціоналу дії і є стійкими щодо збуджень.
Такі конфігурації добре відомі у фізиці конденсованого стану. Наприклад, доменні стінки між областями Всесвіту з різним порушенням симетрії є аналогом доменних стінок у феромагнетиках (звідки й походить їх назва), космічні струни схожі з вихровими лініями в надпровіднику.
Деякі типи неінваріантних вакуумів, які розглядаються теоретиками, наведено нижче[джерело?].
Механічна модель Унру[ред. | ред. код]
Проста механічна модель, запропонована Унру. Розглянемо сукупність олівців, які поставлені торцями на стіл, а гострі кінці яких з'єднані між собою гумками. Така система перебуває в стані нестійкої рівноваги — будь-яке збурення приведе до падіння олівців і переходу з нестабільного стану у стабільний вакуумний стан. Однак напрям падіння є випадковим. Картина рівноважного стану має багато різних варіантів. Звичайно, можливе падіння олівців в одному напрямі. Проте, може статися і так, що навколо деякого олівця всі інші олівці впали в протилежних напрямках. Тоді на центральний олівець зі всіх сторін ізотропно діють однакові сили натягу гумок від олівців, які вже впали. Оскільки сила натягу діє рівномірно, раніше нестабільний вакуумний стан в вибраній точці стає стабільним і олівець не падає. Виникає точка, яка є відмінною від решти точок, в якій симетрія не є порушеною.
Конфігурації вакууму з локально непорушеною калібрувальною симетрією[ред. | ред. код]
Аналогічно як і для механічної моделі, при порушенні калібрувальної симетрії можливі стійкі стани з точково непорушеною симетрією. Такі розв'язки називаються монополями Полякова — т'Хофта[45][46].
При порушенні симетрій певних груп (наприклад [1]) до групи електромагнітної калібрувальної симетрії поле монополя Полякова — т'Хофта є схожим до магнітного поля, тому його ототожнюють з магнітним монополем. В цьому випадку можна показати, що монополь володіє магнітним зарядом кратним , де — елементарний електричний заряд. Можливі також монопольні конфігурації з більшим магнітним зарядом, однак вони розпадаються до монополів з елементарним магнітним зарядом [49]. Конфігурація скалярних і калібрувальних полів для монополя Полякова — т'Хофта може бути вибрана в калібруванні у вигляді , де , — символ Леві-Чівіти, індекс векторного поля є груповим, другий індекс — координатним, — деякі функції, аналітичного вигляду для яких встановити не вдається.
Поле монополя Полякова — т'Хофта в калібруванні для скалярних полів, де — дельта-символ Кронеккера, має вигляд
Кількість монополів, які б мали утворитися внаслідок порушення симетрії Великого Об'єднання становить один монополь на 103 нуклонів, що суперечить спостережуваним даним. Відсутність монополів пояснюється інфляцією. Вважається, що вони були утворені перед фазовим переходом поля з симетрії Великого Об'єднання в симетрію Стандартної моделі, а супроводжуюча цей перехід інфляція привела до розрідження газу монополів[50]. Більше того, відсутність магнітних монополів вважається одним з аргументів на підтримку інфляційної теорії еволюції Всесвіту.
Існують також точкові вакуумні польові конфігурації діони, які володіють як електричним так і магнітним зарядами[51].
Можливі також польові конфігурації з локально непорушеною калібрувальної симетрією більших вимірностей — це одновимірні космічні струни[47] та доменні стінки[48].
Інстантони[ред. | ред. код]
Для нелінійних польових теорій (наприклад квантової хромодинаміки) можливі нетривіальні польові конфігурації в (1+3)-просторі, які називають інстантонами[44]. Вони є певним узагальненням солітона на (1+3)-вимірний простір. Такі конфігурації реалізовують екстремум дії. Вони є непертурбативними (їх неможливо отримати в жодному порядку теорії збурень).
Тим не менше вклад інстантонів і флуктуацій в околі інстантонного стану в твірний функціонал є значним. Інстантони розв'язують -проблему порушення кіральної симетрії[52]. В теорії електрослабких взаємодій саме інстантонні конфігурації слабкого -поля пояснюють порушення баріонного та лептонного чисел[53]. Інстантонні стани відіграють важливу роль і при розпаді фальшивого вакууму (див. нижче)[54][55].
Скірміони[ред. | ред. код]
Ефективні теорії поля з лагранжіанами типу лінійної сигма-моделі добре описують низькоенергетичну мезонну поведінку. Однак для узгодженості розрахунку параметрів взаємодії мезонів при вищих енергіях необхідно лагранжіан доповнювати доданками з вищими степенями по польових похідних
Наявність вищих степенів похідних може дозволяти стійку нетривіальну вакуумну конфігурацію поля, яку називають скірміонами[56].
Скірміони також можуть виникати і у статистичній фізиці[57] і при динамічному порушенні симетрії.
Діагоналізація миттєвого гамільтоніана[ред. | ред. код]
Для неінваріантних вакуумів чітко незрозуміло, що вважати частинкою і чи взагалі можна говорити про частинки у випадку довільної вакуумної конфігурації. В квантовій теорії поля оператор поля представляється як функція операторів породження і знищення , які задовольняють певні (анти)комутаційні співвідношення, вигляд яких залежить від лагранжіана та типу (фермі чи бозе) поля. Якщо відповідний гамільтоніан теорії діагональний по відношенню до цих операторів, то поняття частинки має просту інтерпретацію. Вакуумний стан, що визначається з рівняння , відповідає стану з найменшим власним значенням гамільтоніана, стану без частинок. Частинкою з імпульсом вважається стан .
Однак у випадку залежності гамільтоніана (а отже вакуумного і збуджених станів) від часу виявляється, що стан, який інтерпретується частинкою в даний момент часу, в наступні моменти часу вже частинкою не буде. Тим не менше, можна розвинути простий формалізм у випадку нестаціонарного вакууму — метод діагоналізації миттєвого гамільтоніана[58]. Відповідно до цього методу припускається, що в деякий момент часу, наприклад , діагоналізовано гамільтоніан і знайдено оператори породження і знищення , тут індекс позначає всі квантові числа поля. Пошук такого вакууму можна здійснити, розглядаючи при невзаємодіючі поля і адіабатично вмикаючи взаємодію (параметри взаємодії) за допомогою фактора .
Оператори породження і знищення в усі наступні моменти часу отримуємо за допомогою перетворень Боголюбова
і перетворень, отриманих з даного спряженням (ермітовим чи комплексним). Функції визначаються з умови виконання відповідних комутаційних співвідношень і діагоналізації гамільтоніана в даний момент часу . В даному формалізмі через нееквівалентність вакуумів в різні моменти часу спостерігатиметься народження і знищення частинок під час еволюції (аналог ефекту Унру), кількість частинок, яка народиться до моменту часу рівна
Така корпускулярна інтерпретація неінваріантних вакуумів не є єдино можливою.
Гравітація як хіггс-голдстоунівське поле[ред. | ред. код]
Вперше на можливість трактування гравітона як погдстоуна вказали Гайзенберг та Іваненко[59]. Пізніше така ідея розвивалася з різних точок зору[60][61][62][63][64][65]. В даному розділі подано короткий вступ в проблему.
Калібрувальна гравітація[ред. | ред. код]
Відповідно до сучасних поглядів, поля фундаментальних взаємодій виникають з необхідності інваріантності функції Лагранжа поля матерії відносно локальних калібрувальних перетворень. Як було показано раніше, для включення взаємодії між полем матерії і калібрувальним полем звичайну похідну від поля заміняють на коваріантну похідну. Крім того, калібрувальне поле під дією калібрувальних перетворень змінюється певним чином. Калібрувальні перетворення утворюють компактну групу Лі.
З геометричної точки зору калібрувальні поля представляють собою зв'язності в розшарованому просторі у випадку внутрішніх калібрувальних симетрій — в просторі з локально тривіальним розшаруванням. Розшарований простір узагальнює поняття дотичного розшарування, заміняючи дотичний простір в кожній точці многовиду на довільний векторний простір (наприклад комплексний простір у випадку зарядженого поля Клейна — Ґордона, чи простір лептонної пари (). Таким чином геометрія теорії калібрувальних полів є дуже схожою до теорії відносності.
З іншої сторони, гравітаційне поле слід розглядати як калібрувальне поле з певною групою симетрії. Однак виявляється, що для гравітаційного поля існують дві калібрувальні симетрії. Перша задається загальними коваріантними перетвореннями тензорних величин
які становлять математичне відображення загального принципу відносності Ейнштейна. Ці перетворення утворюють групу .
Однак сам принцип відносності не фіксує ніяким чином (1+3)-вимірну псевдоевклідову структуру простору-часу. Крім того, загально-коваріантні перетворення не враховують іншу симетрію в загальній теорії відносності, а саме симетрію відносно поворотів, бустів і трансляцій в локальних системах відліку (дотичних до просторово-часового многовиду просторах). Для врахування цих фактів в теорію вводиться метричний тензор . Зручно метричний тензор представляти в тетрадному формалізмі , де латинські індекси відображають локальні лоренцівські індекси, тетради задають перехід між загально-коваріантими і локальними лоренцівськими індексами, — тензор Мінковського.
Поле калібрувальної загально-коваріантної симетрії можна легко ототожнити з зв'язністю гравітаційного поля (символами Крістофеля) . Справді, вирази для коваріантної похідної і калібрувальних перетворень зв'язності нагадують аналогічні вирази для поля Янга — Міллса
Проте аналогічного виразу для метричного тензора (тетрадного поля) немає і його калібрувальний статус залишається незрозумілим.
Метрика як хіггс-голдстоунівське поле[ред. | ред. код]
Така ідея в великій мірі розвивалася Іваненком і Сарданашвілі[66][64]. В даному параграфі викладемо основну її суть.
За відсутності гравітаційного поля многовид простору-часу, а також дія матеріальних полів є інваріантними відносно перетворень неоднорідної групи Лоренца. Проте при ввімкненні гравітації, лоренцівська інваріантність системи порушується. Має місце порушення симетрії, де хіггс-голдстоунівське поле асоціюється з метрикою .
Тим не менше, як і у випадку порушення внутрішніх калібрувальних симетрій, в метриці можна виділити Лоренц-інваріантну хіггсівську складову — тензор Мінковського . Відхилення від метрики Мінковського (або що рівноцінно тетради ) відіграють роль голдстоунівських складових. Однак на відміну від картини порушення симетрії поля Янга — Міллса, голдстоунівські гравітаційні поля не можуть занулитися в кожній точці простору-часу яким-небудь вибором калібрування (як було сказано унітарне калібрування занулює голдстоунівські моди тільки для компактних калібрувальних груп Лі). Геометрична причина цього полягає в тому, що локальні перетворення в дотичних просторах діють на похідні як на вектори тільки в плоскому просторі, для якого дотичний простір збігається з ним самим. В кривому просторі векторами відносно локальних перетворень є величини . Таким чином спроба описати весь кривий простір-час виключно хіггсівською метрикою Мінковського приводить лише до переходу у тетрадний формалізм[66].
Гравітація як ефект поляризації вакууму[ред. | ред. код]
Натяком на трактування гравітаційного поля у схожій манері з бозоном Хіггса є можливість отримання лагранжіана гравітаційного поля з врахування поляризації вакууму[67] як було отримано ефективний лагранжіан для поля Хіггса вище. Розглянемо систему полів у кривому просторі, якщо це скалярні невзаємодіючі поля, то відповідна дія має вигляд
де — визначник метричного тензора, — скалярна кривина, — деяка константа, яку з вимоги конформної інваріантності покладають рівною . Якщо внести певний затравочний доданок і додати інтегрування за полем метрики , а потім проінтегрувати по скалярних полях, то можна отримати ефективну дію з якої виділити незалежний від лагранжіан вигляду
де — деякі константи, значення яких залежить від типу , — тензор кривини Рімана, — тензор Річчі, — тензор Вейля. У випадку скалярних полів , , , , , константа виражається через спін поля, константи безмежні при знятті регуляризації константи, які однак можна перенормувати і виразити через космологічну постійну і гравітаційну постійну[66].
Цікаво також, що при деякому наборі констант вільне гравітаційне поле () можна проквантувати, а відповідна теорія є перенормовною[68].
Порушення фальшивого вакууму[ред. | ред. код]
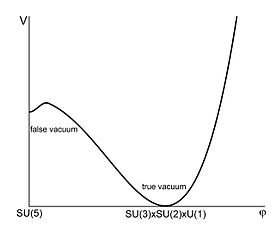
Часто потенціальна енергія (ефективний потенціал у квантовому випадку) має не один мінімум, а декілька. Різним вакуумам відповідають різні енергії. Вакуум з найменшою енергією називають правдивим (істинним), всі решту — неправдивими (фальшивими). Якщо після порушення симетрії і утворення додаткових вакуумів стан системи, який був справжнім вакуумом, став неправдивим, система не перейде одразу в правдивий вакуум (наприклад двохямний потенціал з невеликою ямкою в точці , в якій перебуває система). Якщо яма неглибока, то достатньо інтенсивні зовнішні флуктуації можуть перевести систему в сусідній вакуум з меншою енергією. Якщо ж потенціальна яма достатньо глибока, то перехід системи з метастабільного неправдивого вакууму в істинний відбувається завдяки квантовому тунелюванню.
Динаміка розпаду виглядає наступним бульбашковим чином. В певній точці простору утворюється істинний вакуум, що приводить до утворення такого ж істинного вакууму в усіх сусідніх точках — бульбашка починає рости зі швидкістю світла, поки не зустріне фронт розширення іншої бульбашки. Густина енергії зосереджена в основному на границі бульбашки, всередині бульбашка пуста.
Математично при обчисленні амплітуди переходу вибирається такий контур інтегрування, щоб можна було врахувати наявну інстантонну конфігурацію , яка дає для амплітуди переходу переважний експоненційний фактор , де — значення дії для інстантона[54][55].
Інфляція як розпад несправжнього вакууму[ред. | ред. код]
Десятки факторів вказують на наявність в ранній етап еволюції Всесвіту фази експоненційного розширення — інфляції. З іншого боку, з космологічної моделі Фрідмана випливає, що прискорення , яке отримує тіло під дією гравітації матерії дорівнює
де — гравітаційна стала, — густина енергії та тиск матерії у Всесвіті, — радіус Всесвіту (сфери, всередині якої міститься матерія). Маючи рівняння стану матерії, що пов'язує тиск і густину, можемо обчислити прискорення. Для всіх полів матерії тиск і енергія додатні величини, тому і Всесвіт стискається.
Однак для фізичного вакууму, в якому відбуваються неперервні процеси народження і анігіляції віртуальних пар частинка-античастинка тиск є від'ємним і дорівнює по модулю густині енергії . У такому випадку, за відсутності полів матерії
Тоді, можна показати, що , тобто Всесвіт розширюється експоненційно (розширення де Сіттера).
Однак при охолодженні гарячого Всесвіту в перед-інфляційний період Всесвіт був наповнений квантами полів Великого Об'єднання (наприклад поля ) з густиною г/см3, тобто зовсім не був порожнім. Але Всесвіт достатньо охолов для того, щоб цей вакуум вже був фальшивим (див. рис) і в ньому почали утворюватися бульбашки істинного вакууму розміром ~10−20 см, радіус яких збільшувався зі швидкістю світла. Оскільки всередині бульбашка порожня, то її розміри супроводжувалися експоненційним десіттерівським розширенням. На кінець інфляції розміри бульбашки становили 1032—1040 см (розміри видимого зараз Всесвіту 1028 см, тобто весь видимий Всесвіт повністю вміщується в одній такій бульбашці)[69][70].
Нобелівські премії за дослідження спонтанного порушення симетрії[ред. | ред. код]
В даному розділі вказано лауреатів Нобелівської премії, дослідження яких мало зв'язок чи прямо стосується (2008, 2013) спонтанного порушення симетрії.
- 1979 — Шелдон Лі Глешоу, Стівен Вайнберг та Абдус Салам — «за внесок в об'єднану теорію слабких й електромагнітних взаємодій між елементарними частками, у тому числі передбачення слабких нейтральних струмів».
- 1982 — Кеннет Вільсон — «за теорію критичних явищ у зв'язку з фазовими переходами»
- 1999 — Герард т'Хоофт та Мартінус Вельтман — «за прояснення квантової структури електрослабких взаємодій».
- 2008 — Йоїчіро Намбу — «за відкриття механізму спонтанного порушення симетрії на субатомному рівні» та — Макото Кобаясі і Тосіхіде Масукава — «за встановлення походження симетрії, що передбачає існування в природі щонайменше трьох поколінь кварків».
- 2013 — Франсуа Англер та Пітер Хіггс — «за теоретичне відкриття механізму, який допомагає нам розуміти походження маси субатомних частинок й існування якого було доведено виявленням передбаченої елементарної частинки в експериментах ATLAS і CMS на Великому адронному колайдері в CERN».
Див. також[ред. | ред. код]
Посилання[ред. | ред. код]
- ↑ а б в г д е ж и Weinberg, Steven (1996). The Quantum Theory of Fields. Volume 2. Modern Applications (англ.) . Cambridge University Press. ISBN 0 521 58555 4.
- ↑ Вакарчук, І.О. (2012). Квантова Механіка (укр.) . Львів: ЛНУ ім. І. Франка. Архів оригіналу за 4 червня 2016. Процитовано 10 травня 2016.
- ↑ а б в г Ткачук, В.М. (2011). Фундаментальні Проблеми Квантової Механіки (PDF) (укр.) . Львів: ЛНУ ім. І. Франка. Архів оригіналу (PDF) за 4 червня 2016. Процитовано 10 травня 2016.
- ↑ а б в Peskin M.E., Schroeder D.V. (1995). An introduction to quantum field theory (англ.) . Addison-Wesley Publishing Company.
- ↑ а б Goldstone J., Field theories with «Superconductor» solutions, Nuovo Cimento, 19, 154 (1961).
- ↑ а б Goldstone J., Salam A., Weinberg S., Broken symmetries, Phys. Rev. 127, 965 (1962).
- ↑ а б Higgs H. W., Broken symmetries and the masses of gauge bosons, Phys. Rev. Lett., 13, 598 (1964).
- ↑ Englert F., Brout R., Broken symmetry and the mass of gauge vector mesons, Phys. Rev. Lett., 12, 176 (1964).
- ↑ Weinberg S., General theory of broken local symmetries [Архівовано 27 серпня 2020 у Wayback Machine.], Phys. Rev. D, 7, 1068 (1973).
- ↑ а б Weinberg S., Approximate symmetries and pseudo-Goldstone bosons [Архівовано 8 березня 2021 у Wayback Machine.], Phys. Rev. Lett., 29, 1698 (1972).
- ↑ Dashen R., Chiral SU (3)⊗ SU (3) as a symmetry of the strong interactions [Архівовано 19 січня 2022 у Wayback Machine.], Phys. Rev. 183, 1245 (1969).
- ↑ Боголюбов Н.Н., Ширков Д.В. (1980). Квантовые поля (рос.) . Москва: "Наука".
- ↑ а б Weinberg, Steven (1995). The Quantum Theory of Fields. Volume 1. Foundations (англ.) . Cambridge University Press. ISBN 0 521 55001 7.
- ↑ Goldstone J., Salam A., Weinberg S., Broken symmetries, Phys. Rev. 127, 965 (1962).
- ↑ Славнов А. А., Тождества Уорда в калибровочных теориях, ТМФ, 10, 153 (1972).
- ↑ Taylor J.C., Ward identities and charge renormalization of the Yang-Mills field, Nucl. Phys. B 33, 436 (1971).
- ↑ 't Hooft G., Renormalizable lagrangians for massive Yang-Mills fields, Nucl.Phys.B 35, 167 (1971).
- ↑ Lee B.W., Renormalizable Massive Vector-Meson Theory-Perturbation Theory of the Higgs Phenomenon, Phys. Rev. D 5, 823 (1972).
- ↑ Fujikawa K., Lee B.W., Sanda A., Generalized renormalizable gauge formulation of spontaneously broken gauge theories, Phys. Rev. D 6, 2923 (1972).
- ↑ Faddeev L.D., Popov V.N., Feynman diagrams for the Yang-Mills field, Phys. Lett. B 25, 29 (1967).
- ↑ Nambu Y., Jona-Lasinio G., Dynamical model of elementary particles based on an analogy with superconductivity. I, Phys. Rev. 122, 345 (1961).
- ↑ Nambu Y., Jona-Lasinio G., Dynamical model of elementary particles based on an analogy with superconductivity. II, Phys. Rev. 124, 246 (1961).
- ↑ Jackiw R., Johnson K., Dynamical model of spontaneously broken gauge symmetries, Phys. Rev. D 8, 2386 (1973).
- ↑ Schwinger J., Gauge invariance and mass, Phys. Rev. 123, 397 (1962).
- ↑ Haymaker R.W., Dynamical Symmetry Breaking, Acta Phys. Pol. B 13, 575 (1982).
- ↑ Bjorken J.D., A dynamical origin for the electromagnetic field, Ann. Phys. 24, 174 (1963).
- ↑ а б Гинзбург В. Л., Ландау Л. Д., К теории сверхпроводимости, ЖЭТФ 20, 1064 (1950).
- ↑ Kleinert, Hagen. Gauge Fields in Condensed Matter. Volume 1. Superflow and Vortex Lines, Disorder Fields, Phase Transitions.
- ↑ Hugengolz N., Pines D., Ground-state energy and excitation spectrum of a system of interacting bosons, Phys. Rev. 116, 489 (1959).
- ↑ Xiao-Gang Wen, Zheng-Cheng Gu, Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order, Phys. Rev. B 82, 155138 (2010). [[arxiv:1004.3835|http://arxiv.org/abs/1004.3835 [Архівовано 26 березня 2015 у Wayback Machine.]]]
- ↑ Ровенчак, А.А. (2015). Фізика Бозе-систем. Львів: Видавничий центр ЛНУ ім. І.Франка.
- ↑ Питаевский, Л. П., Вихревые линии в неидеальном бозе-газе, ЖЭТФ 40, 646 (1961).
- ↑ Glashow S.L., Partial-symmetries of weak interactions, Nucl. Phys. 22, 579 (1961).
- ↑ Weinberg S., A model of leptons, Phys. Rev. Lett. 19, 1264 (1967)
- ↑ Salam A., In: Elementary Particle Theory, ed.Svartholm, Almquist and Wiksells, Stockholm, 367.
- ↑ Georgi H., Glashow S., Unity of All Elementary-Particle Forces, Phys. Rev. Lett. 32, 8 (1974)
- ↑ Georgi H., Particles and Fields — 1974, ed. C. Carlson (Amer. Inst. of Physics, N.Y., 1975).
- ↑ Pati J.C., Salam A, Unified lepton-hadron symmetry and a gauge theory of the basic interactions, Phys. Rev. D. 8, 1240 (1973).
- ↑ а б Witten E., Dynamical breaking of supersymmetry, Nucl. Phys. B., 188, 513 (1981).
- ↑ Wess J., Zumino B., Supergauge transformations in four dimensions, Nucl. Phys. B 70, 139 (1974).
- ↑ Волков Д. В., Сорока В. А., Эффект Хиггса для голдстоуновских частиц со спином 1/2, Письма в ЖЭТФ, 18, 529 (1973).
- ↑ Deser S. and Zumino B., Broken supersymmetry and supergravity, Phys. Rev. Lett. 38, 1433 (1977).
- ↑ O'Raifeartaigh L., Spontaneous symmetry breaking for chirals scalar superfields, Nucl. Phys. B 96, 331 (1975).
- ↑ а б Belavin A.A., Polyakov A.M., Schwarz A.S., Tyupkin Yu.S., Pseudoparticle solutions of the Yang-Mills equations, Phys. Lett. B 59, 85 (1975).
- ↑ а б Поляков А, М., Спектр частиц в квантовой теории поля, Письма в ЖЭТФ 20, 430 (1974).
- ↑ а б 't Hooft, G., Magnetic monopoles in unified gauge theories, Nucl. Phys. B. 79, 276 (1974).
- ↑ а б Nielsen H., Oleson P., Vortex-line models for dual strings, Nucl. Phys. B 61, 45 (1973).
- ↑ а б Зельдович Я. Б., Кобзарев И. Ю., Окунь Л. Б., Космологические следствия спонтанного нарушения дискретной симметрии, ЖЭТФ 40, 2 (1975).
- ↑ Богомольный Е. Б., Устойчивость классических решений, Ядерная Физика, 861 (1976).
- ↑ Zeldovich Y.B., Khlopov M.Y., On the concentration of relic magnetic monopoles in the universe, Phys. Lett. B 79, 239 (1978).
- ↑ Julia B., Zee A., Poles with both magnetic and electric charges in non-Abelian gauge theory, Phys.Rev. D 11, 2227 (1975).
- ↑ 't Hooft G., Computation of the quantum effects due to a four-dimensional pseudoparticle, Phys. Rev. D 14, 3432 (1976).
- ↑ 't Hooft G., Symmetry breaking through Bell-Jackiw anomalies, Phys. Rev. Lett. 37, 8 (1976).
- ↑ а б Coleman S., Fate of the false vacuum: Semiclassical theory, Phys. Rev. D 15, 2929 (1977), http://journals.aps.org/prd/abstract/10.1103/PhysRevD.15.2929 [Архівовано 26 березня 2015 у Wayback Machine.]
- ↑ а б Coleman S., Callan C.G., Fate of the false vacuum. II. First quantum corrections, Phys. Rev. D 16, 1762 (1977). http://journals.aps.org/prd/abstract/10.1103/PhysRevD.16.1762 [Архівовано 3 червня 2019 у Wayback Machine.]
- ↑ Skyrme T.H.R., A non-linear field theory, Proc. Roy. Soc. London A 260, 127 (1961).
- ↑ Khawaja U.A., Stoof H., Skyrmions in a ferromagnetic Bose–Einstein condensate, Nature 411, 918 (2001).
- ↑ Гриб А. А., Мамаев С. Г.. Мостепаненко В. М., Квантовые эффекты в интенсивных внешних полях, Москва: Атомиздат, 1980.
- ↑ Ivanenko, D. D. (1970). In: Physics, Logic and History. New York.
- ↑ Joseph A., Solomon A.I., Global and infinitesimal nonlinear chiral transformations, J. Math. Phys. 11, 748 (1970).
- ↑ Isham C.J., Salam A., Strathdee J., Nonlinear realizations of space-time symmetries. Scalar and tensor gravity, Ann. Phys. 62, 98 (1971).
- ↑ Огиевецкий В. И., Полубаринов И. В., ЖЭТФ 21, 1093 (1965).
- ↑ Ne'eman Y., Sherry T.N., Graded spin-extension of the algebra of volume-preserving deformations, Phys. Lett. B 76, 413 (1978).
- ↑ а б Сарданашвили Г. А. (1998), Докторская диссертация «Хиггсовская модель классического гравитационного поля», http://www.g-sardanashvily.ru/D.Sc-Sard.pdf
- ↑ Sardanashvily G. (2016), Lecture on gauge gravitation theory. Gravity as a Higgs field, arXiv:1602.06776. http://arxiv.org/pdf/1602.06776v1.pdf [Архівовано 4 червня 2016 у Wayback Machine.]
- ↑ а б в Иваненко Д.Д., Пронин П.И., Сарданашвили Г.А (1985). Калибровочная Теория Гравитации (рос.) . Москва: Издательство МГУ.
- ↑ Adler S., Einstein Gravity as a Symmetry Breaking Effect in Quantum Field Theory, Rev. Mod. Phys. 54, 729 (1982).
- ↑ Stelle K., Renormalization of Higher-Derivative Quantum Gravity, Phys. Rev. D 16, 953 (1977).
- ↑ Linde A. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems // Phys. Lett. — 1982. — Т. 108, вип. 389.
- ↑ Albrecht A., Steinhardt P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking // Phys. Rev. Lett.. — 1982. — Т. 48, вип. 1220. — DOI:.
|
|
Ця стаття належить до добрих статей української Вікіпедії. |

































































































![{\displaystyle F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+\left[A_{\mu },A_{\nu }\right]^{a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ef89537579afc7db9f65e762be036ff55d6fd3a)












































![{\displaystyle {\frac {\partial V}{\partial \varphi _{i}}}\left(\varphi _{0}+\lambda \varphi _{0}^{(1)}\right)=0\Rightarrow {\frac {\partial V_{0}(\varphi _{0})}{\partial \varphi _{i}}}+\lambda \left[{\frac {\partial V_{1}(\varphi _{0})}{\partial \varphi _{i}}}+{\frac {\partial ^{2}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}\varphi _{0,j}^{(1)}\right]=\lambda \left[{\frac {\partial V_{1}(\varphi _{0})}{\partial \varphi _{i}}}+{\frac {\partial ^{2}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}\varphi _{0,j}^{(1)}\right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14e883fa0730641bce233b926d199959eba8c8aa)





![{\displaystyle (m^{2})^{kl}=({e}^{k})_{i}({e}^{l})_{j}{\frac {\partial ^{2}V}{\partial \varphi _{i}\partial \varphi _{j}}}\left(\varphi _{0}+\lambda \varphi _{0}^{(1)}\right)=\lambda ({e}^{k})_{i}({e}^{l})_{j}\left[{\frac {\partial ^{2}V_{1}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}+{\frac {\partial ^{3}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}\partial \varphi _{n}}}\varphi _{0,n}^{(1)}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a540b4c2c6044a00bfa3588affc57feb6c7298e2)












![{\displaystyle Z=\int [d\varphi ][d\psi ][...]e^{iS[\varphi ,\psi ,...]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/521e5b0185d79880b2765e642ee4eec3fe019b36)




![{\displaystyle Z[J]=\exp {(iW[J])},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eda57fb1d481a79ed04a722a9df56d5d7b2f851)
![{\displaystyle W[J]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ebdc65f8e1fc5204380a81951ea53868aca978)

![{\displaystyle \varphi _{J}^{i}(x)={\frac {\delta }{\delta J_{i}(x)}}W[J].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0154f5ffb03b210196d5dec34ac6e596fec24144)

![{\displaystyle \Gamma [\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/587eaacd4d52359919a54d4e5abd67b8dd6b2c80)
![{\displaystyle \Gamma [\varphi ]=-\int d^{4}x\varphi ^{i}(x)J_{i,\varphi }(x)+W[J].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9923a7cc0a6569244eafd2def86b326d1af63864)
![{\displaystyle {\frac {\delta \Gamma [\varphi ]}{\delta \varphi ^{i}(x)}}=-J_{i}(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63a1335ad4d3a30880d74446375c6c5d475d9e4a)

![{\displaystyle {\frac {\delta \Gamma [\varphi ]}{\delta \varphi ^{i}(x)}}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9cdcc5fcacf1fb20a58b85231f93c790d57369)
![{\displaystyle \Gamma [\varphi ]=-{\mathcal {V}}_{4}V(\varphi ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b3efe12ccea52c4bb3b9b61ef6997fc54fb7f8d)





















![{\displaystyle Z=C\int ({\mathcal {D}}A)({\mathcal {D}}\phi )\exp \left[i\int d^{4}x({\mathcal {L}}(A,\phi )-{\frac {1}{2}}G^{2})\right]\det \left({\frac {\delta G}{\delta \alpha }}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f88409f42ddf2b61bb03fcf5ca55339ebfe5742)
![{\displaystyle {\mathcal {L}}\approx -{\frac {1}{2}}A_{\mu }^{a}\left(\delta ^{ab}\left[-\eta ^{\mu \nu }\partial ^{2}+(1-{\frac {1}{\xi }}\partial ^{\mu }\partial ^{\nu })\right]-\eta ^{\mu \nu }(m_{A}^{2})_{ab}\right)A_{\nu }^{b}+{\frac {1}{2}}(\partial _{\mu }\phi )^{2}-{\frac {1}{2}}(m_{G}^{2})_{ij}\phi _{i}\phi _{j}+{\frac {1}{2}}(\partial _{\mu }{\widetilde {\phi }})^{2}-{\frac {1}{2}}(m_{H}^{2})_{ij}{\widetilde {\phi }}_{i}{\widetilde {\phi }}_{j},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d47e4924b8f5240a9864a57056e9233405cf34)
















![{\displaystyle [{\widehat {I}}_{a},q]=-t_{a}q,\;[{\widehat {X}}_{a},q]=-\gamma ^{5}t_{a}q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eef661145b5372a6598f82fa66af4ab73f50f05)




![{\displaystyle S[\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db5fdc195e3f0d76fb555087c3712f5bf8936e13)

![{\displaystyle S[\varphi ,\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1274ba9c4cd6fddf416cbccc0ad2dfc64c66044)
![{\displaystyle Z_{\sigma }=\int [d\varphi ]e^{iS[\varphi ,\sigma ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebcf2141e54d2ac0c44e3ef2f287c43469748bf7)

![{\displaystyle Z=\int [d\varphi ][d\sigma ]e^{iS[\varphi ,\sigma ]+iS_{\sigma }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe482bc24c206bdaab5a1a2cb971586b2f42bc71)
![{\displaystyle Z=\int [d\varphi ][d\sigma ]e^{iS[\varphi ,\sigma ]+iS_{\sigma }}=\int [d\sigma ]e^{iS_{eff}+iS_{\sigma }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca8f3bab49f57e4c8890fa85add40b0a89b667c)


![{\displaystyle Z=e^{-\beta F[\varphi ]}=\int ({\mathcal {D}}\varphi )\exp {\left(-\beta \int d^{3}x\left[e(x)-\mu (T)\varphi ^{\dagger }\varphi \right]\right)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47d0f21a7873b454d890bf9112ceb699ffecd065)





![{\displaystyle F\approx E=\int d^{3}x\left[e(x)-\mu \varphi ^{\dagger }\varphi \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f45fc0651eda3147c3c1c4ec26778106437532a)
















![{\displaystyle \epsilon =\int d^{3}x\left[{\frac {1}{2}}\left((\nabla \rho (x))^{2}+(-2m^{2})\rho (x)^{2}\right)+{\frac {1}{2}}a^{2}(\nabla \gamma (x))^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d1305f187a501b5935f392bd8b386a01b8e4dc6)































![{\displaystyle {\mathcal {L}}=-{\frac {1}{4}}(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })^{2}-{\frac {1}{4}}(\partial _{\mu }Z_{\nu }-\partial _{\nu }Z_{\mu })^{2}+m_{Z}^{2}Z^{2}-\sum _{i=\pm }\left[{\frac {1}{4}}(\partial _{\mu }W_{\nu }^{i}-\partial _{\nu }W_{\mu }^{i})^{2}+m_{W}^{2}(W^{i})^{2}\right]+(\partial _{\mu }\phi )^{2}-m_{\phi }^{2}\phi ^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62057dc536d6f6b604eeb2fd5ec84b7097798a6a)






































![{\displaystyle \langle \delta \varphi \rangle _{0}=\langle \left[\varphi ,Q_{\alpha }\right]\rangle _{0}\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2092869cdaf11d2050bf0b056e7194ef97b34f0e)








































































![{\displaystyle {\mathcal {L}}_{gr}={\sqrt {-g}}\left[-A+BR+CR_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }+DR_{\mu \nu }R^{\mu \nu }+E\partial ^{2}R+FR+GC_{\alpha \beta \mu \nu }C^{\alpha \beta \mu \nu }\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0859d19f5a19dcaf7cae0f5d210773a7394b56e1)













![{\displaystyle \exp {(-S[\varphi _{inst}])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8eab1545b24ffc4376b0efc8c9cb97fa15bc4e8)
![{\displaystyle S[\varphi _{inst}]>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf50aff3ae3ad2d6310678ea7ac87eeda99aa47)







