Коефіцієнт кореляції Пірсона


У статистиці, коефіціє́нт кореля́ції Пі́рсона (ККП, англ. Pearson correlation coefficient, PCC)[a] — це коефіцієнт кореляції, який вимірює лінійну[en] кореляцію між двома наборами даних. Це відношення коваріації двох змінних до добутку їхніх стандартних відхилень; таким чином, це, по суті, унормована міра коваріації, така, що її результат завжди має значення між −1 та 1. Як і сама коваріація, ця міра може відображувати лише лінійну кореляцію змінних, і не враховує багатьох інших типів взаємозв'язків і кореляцій. Як простий приклад, можна було би очікувати, що вік і зріст групи підлітків із середньої школи матимуть коефіцієнт кореляції Пірсона значно більший за 0, але менший за 1 (оскільки 1 означало би нереалістично ідеальну кореляцію).
Назва й історія[ред. | ред. код]
Розробив його Карл Пірсон на основі спорідненої ідеї, запропонованої Френсісом Гальтоном у 1880-х роках, математичну формулу для якої вивів та опублікував Огюст Браве 1844 року.[b][6][7][8][9] Назва цього коефіцієнта є одним із прикладів закону Стіглера.
Визначення[ред. | ред. код]
Коефіцієнт кореляції Пірсона це коваріація двох змінних, поділена на добуток їхніх стандартних відхилень. Вигляд цього визначення містить «момент добутку», тобто середнє значення (перший момент відносно початку координат) добутку змінних, скоригованих на їхні середні значення; тому в назві й використовують означення «моменту добутку».
Для сукупності[ред. | ред. код]
Коефіцієнт кореляції Пірсона, коли його застосовують до сукупності, зазвичай позначують грецькою літерою ρ (ро), й можуть називати коефіцієнтом кореляції сукупності (англ. population correlation coefficient) або коефіцієнтом кореляції Пірсона для сукупності (англ. population Pearson correlation coefficient). Для пари випадкових змінних (наприклад, Зріст та Вага), формулою для ρ[10] є[11]
де
- — коваріація
- — стандартне відхилення
- — стандартне відхилення .
Формулу для можливо виразити через середнє значення та математичне сподівання. Оскільки[10]
формулу для також можливо записати як
де
- та визначено як вище
- — середнє значення
- — середнє значення
- — математичне сподівання.
Формулу для можливо виразити через нецентровані моменти. Оскільки
формулу для також можливо записати як
Для вибірки[ред. | ред. код]
Коефіцієнт кореляції Пірсона, коли його застосовують до вибірки, зазвичай позначують через і можуть називати коефіцієнтом кореляції вибірки (англ. sample correlation coefficient) або коефіцієнтом кореляції Пірсона для вибірки (англ. sample Pearson correlation coefficient). Формулу для можливо отримати, підставивши оцінки коваріацій та дисперсій на основі вибірки до наведеної вище формули. Для парних даних , що складаються з пар, визначають як
де
- — розмір вибірки
- — окремі точки вибірки з індексом i
- (середнє значення вибірки); й аналогічно для .
Перегрупування дає таку формулу для :
де визначено як вище.
Ця формула пропонує зручний однопрохідний алгоритм обчислення кореляцій вибірок, хоча, залежно від задіяних чисел, вона іноді може бути чисельно нестійкою.
Подальше перегрупування дає таку[10] формулу для :
де визначено як вище.
Еквівалентний вираз дає формулу для як середнє добутків стандартних оцінок наступним чином:
де
- визначено як вище, а визначено нижче
- — стандартна оцінка (й аналогічно для стандартної оцінки ).
Доступні й альтернативні формули для . Наприклад, можливо використовувати наступну формулу для :
де
- визначено як вище, а
- (ви́біркове стандартне відхилення); й аналогічно для .
Для спільно гауссових розподілів[ред. | ред. код]
Якщо спільно гауссові, з нульовим середнім значенням і дисперсією , то .
Практичні проблеми[ред. | ред. код]
В умовах сильного шуму виділяння коефіцієнта кореляції між двома наборами стохастичних змінних нетривіальне, особливо коли канонічно-кореляційний аналіз показує зниження значень кореляції через значний внесок шуму. Узагальнення цього підходу наведено в іншому місці.[12]
У випадку відсутності даних, Ґаррен вивів оцінювання максимальною правдоподібністю.[13]
Деякі розподіли (наприклад, стійкі розподіли, відмінні від нормального) не мають визначеної дисперсії.
Математичні властивості[ред. | ред. код]
Значення коефіцієнта кореляції Пірсона як для вибірки, так і для сукупності перебувають на або між −1 та 1. Кореляції, які дорівнюють +1 чи −1, відповідають точкам даних, що лежать точно на прямій (у випадку коефіцієнта кореляції вибірки), або двовимірному розподілу, носій[en] якого лежить на прямій (у випадку коефіцієнта кореляції сукупності). Коефіцієнт кореляції Пірсона симетричний: corr(X,Y) = corr(Y,X).
Ключовою математичною властивістю коефіцієнта кореляції Пірсона є його інваріантність[en] щодо окремих змін розташування та масштабу в обох змінних. Тобто ми можемо перетворити X на a + bX, і перетворити Y на c + dY, де a, b, c, та d сталі, а b, d > 0, не змінивши коефіцієнта кореляції. (Це справджується як для коефіцієнта кореляції сукупності, так і для коефіцієнта кореляції вибірки.) Загальніші лінійні перетворення кореляцію змінюють: щодо того, як це застосовувати, див. § Декореляція n випадкових змінних.
Тлумачення[ред. | ред. код]
Коефіцієнт кореляції набуває значень з −1 по 1. Абсолютне рівне значення 1 означає, що лінійне рівняння описує взаємозв'язок між X та Y ідеально, з усіма точками даних на одній прямій. Знак кореляції визначається нахилом регресії: значення +1 означає, що всі точки даних лежать на прямій, за якої Y зростає зі зростанням X, і навпаки для −1.[14] Значення 0 означає, що між змінними немає лінійної залежності.[15]
Загальніше, (Xi − X)(Yi − Y) додатний тоді й лише тоді, коли Xi та Yi перебувають з одного боку від своїх середніх значень. Відтак, коефіцієнт кореляції додатний, коли Xi та Yi схильні бути одночасно більшими або одночасно меншими за свої середні значення. Коефіцієнт кореляції від'ємний (антикореляція[en]), коли Xi та Yi схильні перебувати по різні боки від своїх середніх значень. Більше того, що сильніша будь-яка з цих тенденцій, то більше абсолютне значення коефіцієнта кореляції.
Роджерс та Найсвандер[16] перелічили тринадцять способів тлумачення кореляції або простих функцій від неї:
- Функція від сирих оцінок та середніх значень
- Стандартизована коваріація
- Стандартизований нахил лінії регресії
- Геометричне середнє двох нахилів регресії
- Квадратний корінь відношення двох дисперсій
- Середній векторний добуток стандартизованих змінних
- Функція кута між двома стандартизованими регресійними лініями
- Функція кута між двома векторами змінних
- Перемасштабована дисперсія різниці стандартизованих оцінок
- Оцінка за правилом повітряної кульки
- Пов'язана з двовимірними еліпсами ізоконцентрації
- Функція статистичного критерію із запланованих експериментів
- Відношення двох середніх
Геометричне тлумачення[ред. | ред. код]

Для нецентрованих даних існує зв'язок між коефіцієнтом кореляції та кутом φ між двома регресійними лініями, y = gX(x) та x = gY(y), отриманими в результаті регресії y на x та x на y відповідно. (Тут φ відкладають проти годинникової стрілки в першому квадранті, утвореному навколо точки перетину ліній, якщо r > 0, чи проти годинникової стрілки з четвертого до другого квадранту, якщо r < 0.) Можливо показати,[17] що якщо стандартні відхилення рівні, то r = sec φ − tg φ, де sec та tg — тригонометричні функції.
Для центрованих даних (тобто даних, зміщених на середні значення їхніх відповідних змінних, таким чином, щоби середнє значення кожної змінної було нульовим) коефіцієнт кореляції також можливо розглядати як косинус кута θ між двома спостережуваними векторами в N-вимірному просторі (для N спостережень кожної змінної).[18]
Коефіцієнти як нецентрованої (не пірсоново сумісної), так і центрованої кореляції можливо визначати для набору даних. Наприклад, припустімо, що виявлено, що п'ять країн мають валовий національний продукт 1, 2, 3, 5 та 8 мільярдів доларів відповідно. Припустімо, що ці ж п'ять країн (у тому ж порядку) мають 11 %, 12 %, 13 %, 15 % та 18 % бідності. Тоді нехай x та y будуть впорядкованими 5-елементними векторами, що містять наведені вище дані: x = (1, 2, 3, 5, 8) та y = (0.11, 0.12, 0.13, 0.15, 0.18).
За звичайною процедурою визначення кута θ між двома векторами (див. скалярний добуток) коефіцієнт нецентрованої кореляції становить
Цей коефіцієнт нецентрованої кореляції ідентичний косинусній подібності. Наведені вище дані було свідомо обрано так, щоби вони бути ідеально корельованими: y = 0.10 + 0.01 x. Тому коефіцієнт кореляції Пірсона мусить дорівнювати рівно одиниці. Центрування даних (зміщення x на ℰ(x) = 3.8 та y на ℰ(y) = 0.138) дає x = (−2.8, −1.8, −0.8, 1.2, 4.2) та y = (−0.028, −0.018, −0.008, 0.012, 0.042), звідки
як і очікувалося.
Тлумачення розміру кореляції[ред. | ред. код]
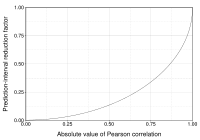
Декілька авторів запропонували настанови для тлумачення коефіцієнта кореляції.[19][20] Проте всі такі критерії дещо довільні.[20] Тлумачення коефіцієнта кореляції залежить від контексту та цілей. Кореляція 0,8 може бути дуже низькою, якщо йдеться про перевірку фізичного закону з використанням високоякісних інструментів, але може вважатися дуже високою в соціальних науках, де внесок від ускладнювальних чинників може бути більшим.
Висновування[ред. | ред. код]
Статистичне висновування на основі коефіцієнті кореляції Пірсона часто зосереджується на одній з наступних двох цілей:
- Одна мета полягає в перевірці нульової гіпотези, що істинний коефіцієнт кореляції ρ дорівнює 0, на основі значення коефіцієнта кореляції вибірки r.
- Інша мета полягає в тому, щоби вивести довірчий інтервал, який при повторюваному вибиранні має задану ймовірність містити ρ.
Методи досягнення однієї або обох цих цілей обговорюються нижче.
Використання перестановкового критерію[ред. | ред. код]
Перстановкові критерії забезпечують прямий підхід до здійснення перевірок гіпотез і побудови довірчих інтервалів. Перестановковий критерій для коефіцієнта кореляції Пірсона містить наступні два кроки:
- Використовуючи первинні паровані дані (xi, yi), випадково визначити пари заново, створивши новий набір даних (xi, yi′), де i′ — перестановка множини {1,…,n}. Перестановку i′ вибирають випадково, з рівними ймовірностями для всіх n! можливих перестановок. Це рівнозначне вибиранню i′ випадково без повторів з множини {1, …, n}. У натяжці, тісно пов'язаному підході, i та i′ є рівними й вибираються з {1, …, n} з повторами;
- Побудувати коефіцієнт кореляції r з цих увипадковлених даних.
Щоби виконати перевірку перестановкового критерію, повторіть кроки (1) та (2) велику кількість разів. p-значення для перестановкового критерію — це частка значень r, породжених на кроці (2), більших за коефіцієнт кореляції Пірсона, обчислений із первинних даних. Тут «більший» може означати як більший за абсолютним значенням, так і більший за значенням зі знаком, залежно від того, чи потрібен двобічний[en], чи однобічний[en] критерій.
Використання натяжки[ред. | ред. код]
Для побудови довірчих інтервалів для коефіцієнта кореляції Пірсона можливо використовувати натяжку. В «непараметричній» натяжці n пар (xi, yi) перевибирають зі спостережуваного набору з n пар «з повторами», й коефіцієнт кореляції r обчислюють на основі цих перевибраних даних. Цей процес повторюють велику кількість разів, і цей емпіричний розподіл перевибраних значень r використовують для наближення вибіркового розподілу цієї статистики. 95 %-вий довірчий інтервал для ρ можливо визначити як інтервал, що простягається від 2,5-го до 97,5-го перцентиля перевибраних значень r.
Стандартна похибка[ред. | ред. код]
Якщо та — випадкові змінні, то стандартною похибкою, пов'язаною з кореляцією у випадку нульової гіпотези, є
де — кореляція (за припущення r≈0), а — розмір вибірки.[21][22]
Перевірка з використанням розподілу Ст'юдента[ред. | ред. код]
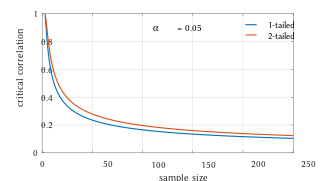
Для пар з некорельованого двовимірного нормального розподілу, вибірковий розподіл ст'юдентованого коефіцієнта кореляції Пірсона дотримується t-розподілу Ст'юдента зі ступенями вільності n − 2. Зокрема, якщо змінні в основі мають двовимірний нормальний розподіл, то змінна
у випадку нульової гіпотези (нульової кореляції) має розподіл Ст'юдента.[23] Це приблизно виконується у випадку не нормальних спостережуваних значень, якщо розміри вибірок достатньо великі.[24] Для визначення критичних значень для r потрібна обернена функція:
Також можливо використовувати асимптотичні підходи для великих вибірок.
Інша рання стаття[25] пропонує графіки та таблиці для загальних значень ρ, для малих розмірів вибірки, та обговорює підходи до обчислень.
У випадку, якщо змінні в основі не нормальні, вибірковий розподіл коефіцієнта кореляції Пірсона дотримується розподілу Ст'юдента, але ступені вільності знижуються.[26]
Використання точного розподілу[ред. | ред. код]
Для даних, що слідують двовимірному нормальному розподілу, точною функцією густини f(r) для вибіркового коефіцієнта кореляції r нормального двовимірного розподілу є[27][28][29]
де — це гамма-функція, а — гауссова гіпергеометрична функція.
В окремому випадку, коли (нульова кореляція в сукупності), точну функцію густини f(r) можливо записати як
де — це бета-функція, що є одним зі способів запису густини t-розподілу Ст'юдента для ст'юдентованого вибіркового коефіцієнта кореляції, як зазначено вище.
Використання точного довірчого розподілу[ред. | ред. код]
Довірчі інтервали та критерії можливо розраховувати з довірчого розподілу[en]. Точна довірча густина для ρ становить[30]
де — це гауссова гіпергеометрична функція, а .
Використання перетворення Фішера[ред. | ред. код]
На практиці обчислення довірчих інтервалів та перевірки гіпотез щодо ρ зазвичай виконують за допомогою перетворення Фішера[en], :
F(r) приблизно дотримується нормальному розподілу, де
де n — розмір вибірки. Похибка наближення найнижча для великого розміру вибірки і малих значень та , і збільшується в іншому випадку.
За використання цього наближення z-оцінка становить
за нульовою гіпотезою, що , за припущення, що пари вибірки незалежні й однаково розподілені та дотримуються двовимірного нормального розподілу. Відтак, можливо отримати наближене p-значення з таблиці нормальної ймовірності. Наприклад, якщо спостерігається z = 2.2 й потрібне двобічне p-значення для перевірки нульової гіпотези, що , то p-значення становитиме 2 Φ(−2.2) = 0.028, де Φ — це стандартна нормальна функція розподілу.
Щоб отримати довірчий інтервал для ρ, спочатку обчислімо довірчий інтервал для F():
Обернене перетворення Фішера повертає інтервал до шкали кореляції.
Наприклад, припустімо, що ми спостерігаємо r = 0.7 з розміром вибірки n=50, і хочемо отримати 95 %-вий довірчий інтервал для ρ. Перетворене значення становить , тому довірчий інтервал у перетвореній шкалі становить , або (0.5814, 1.1532). Перетворення назад до шкали кореляції дає (0.5237, 0.8188).
В регресійному аналізі методом найменших квадратів[ред. | ред. код]
Квадрат коефіцієнта кореляції вибірки зазвичай позначують через r2, він є окремим випадком коефіцієнта детермінації. У цьому випадку він оцінює частку дисперсії Y, яку пояснює X через просту лінійну регресію. Отже, якщо є спостережуваний набір даних та допасований набір даних , то як відправну точку повну дисперсію Yi навколо їхнього середнього значення можливо розкласти як
де — це допасовані значення з регресійного аналізу. Це можливо переформулювати як
Обидва доданки вище — це частка дисперсії в Y, яку пояснює X (правий), та яку X не пояснює (лівий).
Далі, ми застосовуємо властивість регресійних моделей найменших квадратів, що вибіркова коваріація між та нульова. Тож вибірковий коефіцієнт кореляції між спостережуваними та допасованими значеннями відгуку в регресії можливо записати (обчислення виконується виходячи з очікування гауссової статистики) як
Тож
де — частка дисперсії Y, пояснювана лінійною функцією X.
У наведеному вище виведенні той факт, що
можливо довести, відмітивши, що частинні похідні залишкової суми квадратів[en] (RSS) за β0 та β1 у моделі найменших квадратів дорівнюють 0, де
- .
Кінець кінцем, рівняння можливо записати як
де
- .
Символ називають сумою квадратів регресії, також відомою як пояснена сума квадратів, а — повна сума квадратів[en] (пропорційна дисперсії даних).
Чутливість до розподілу даних[ред. | ред. код]
Існування[ред. | ред. код]
Коефіцієнт кореляції Пірсона для сукупності визначено через моменти, й тому він існує для будь-якого двовимірного розподілу ймовірності, для якого визначені коваріація сукупності та відособлені дисперсії сукупності, й вони ненульові. Деякі розподіли ймовірності, такі як розподіл Коші, мають невизначену дисперсію, й відтак якщо X або Y відповідають такому розподілові, то ρ невизначений. У деяких практичних застосуваннях, дані в яких підозрюють на відповідність розподілові з повільно спадним хвостом[en], це важливий аспект. Проте, існування коефіцієнта кореляції зазвичай не проблема; наприклад, якщо діапазон розподілу обмежений, ρ завжди визначений.
Розмір вибірки[ред. | ред. код]
- Якщо розмір вибірки помірний або великий і сукупність нормальна, то у випадку двовимірного нормального розподілу вибірковий коефіцієнт кореляції є максимально-правдоподібнісною оцінкою коефіцієнта кореляції сукупності, асимптотично[en] незміщеною[en] та ефективною[en], що приблизно означає неможливість побудувати оцінку, точнішу за вибірковий коефіцієнт кореляції.
- Якщо розмір вибірки великий і сукупність не нормальна, то вибірковий коефіцієнт кореляції залишається приблизно незміщеним, але може не бути ефективним.
- Якщо розмір вибірки великий, то вибірковий коефіцієнт кореляції є слушною оцінкою коефіцієнта кореляції сукупності, за умови, що середні значення вибірки, дисперсії та коваріація слушні (що гарантовано, коли можливо застосувати закон великих чисел).
- Якщо розмір вибірки малий, то вибірковий коефіцієнт кореляції r не є незміщеною оцінкою ρ.[10] Замість цього слід використовувати скоригований коефіцієнт кореляції: визначення див. далі у цій статті.
- Кореляції можуть бути різними для незбалансованих дихотомних даних, коли у вибірці є помилка дисперсії.[31]
Робастність[ред. | ред. код]
Як і багато інших часто використовуваних статистик, вибіркова статистика r не робастна,[32] тож за наявності викидів її значення може бути оманливим.[33][34] Зокрема, коефіцієнт кореляції моменту добутку не робастний ані щодо розподілу,[35] ані щодо викидів[32] (див. Робастність у статистиці § Поняття робастності). Перевірка діаграми розсіяння між X та Y зазвичай виявляє ситуацію, коли робастність може бути проблемою, і в таких випадках може бути рекомендовано використовувати робастну міру пов'язаності. Проте слід зазначити, що хоч більшість робастних оцінювачів пов'язаності і вимірюють якимось чином статистичну залежність, вони зазвичай не інтерпретовні тою ж мірою, що й коефіцієнт кореляції Пірсона.
Статистичне висновування для коефіцієнта кореляції Пірсона чутливе до розподілу даних. Точні критерії та асимптотичні критерії на основі перетворення Фішера[en] можливо застосовувати, якщо дані розподілені приблизно нормально, але в іншому разі вони можуть бути оманливими. У деяких ситуаціях можливо використовувати натяжку для створення довірчих інтервалів, а перестановкові критерії — для здійснення перевірки гіпотез. Ці непараметричні[en] підходи можуть давати змістовніші результати в деяких ситуаціях, коли двовимірна нормальність не виконується. Проте стандартні версії цих підходів покладаються на взаємозамінність[en] даних, що означає, що не існує впорядкування чи групування аналізованих пар даних, які могли би вплинути на поведінку оцінки кореляції.
Стратифікований аналіз — це один зі способів або пристосування до відсутності двовимірної нормальності, або для відокремлення кореляції, що випливає з одного чинника при контролі над іншим. Якщо W подає приналежність до кластеру або інший чинник, який хочеться контролювати, можливо стратифікувати дані на основі значення W, а потім обчислити коефіцієнт кореляції в межах кожної страти. Оцінки на рівні страт потім можливо об'єднати для оцінки загальної кореляції при контролі над W.[36]
Варіанти[ред. | ред. код]
Існують різні варіації коефіцієнта кореляції, які можливо обчислювати для різних цілей. Ось декілька прикладів.
Скоригований коефіцієнт кореляції[ред. | ред. код]
Вибірковий коефіцієнт кореляції r не є незміщеною оцінкою ρ. Для даних, що дотримуються двовимірному нормальному розподілу, математичне сподівання E[r] вибіркового коефіцієнта кореляції r нормальної двовимірності становить[37]
- тож r є зміщеним оцінювачем
Унікальний мінімально-дисперсійний незміщений оцінювач (англ. unique minimum variance unbiased estimator) radj задається як[38]
-
()
де:
- визначено як вище,
- — гауссова гіпергеометрична функція.
Приблизно незміщений оцінювач (англ. approximately unbiased estimator) radj можливо отримати[джерело?] шляхом утинання E[r] та розв'язання цього утятого рівняння:
-
()
Приблизним розв'язком[джерело?] рівняння (2) є
-
()
де у (3)
- визначено як вище,
- radj — субоптимальний оцінювач,[джерело?][прояснити: ком.]
- radj також можливо отримати максимізуванням log(f(r)),
- radj має мінімальну дисперсію за великих значень n,
- radj має зміщення порядку 1⁄(n − 1).
Іншим запропонованим[10] скоригованим коефіцієнтом кореляції (англ. adjusted correlation coefficient) є[джерело?]
radj ≈ r за великих значень n.
Коефіцієнт зваженої кореляції[ред. | ред. код]
Покладімо, що спостереження, які потрібно скорелювати, мають різні ступені важливості, які можливо виразити ваговим вектором w. Щоб обчислити кореляцію між векторами x та y з ваговим вектором w (всі довжиною n),[39][40]
- Зважене середнє:
- Зважена коваріація:
- Зважена кореляція (англ. weighted correlation):
Віддзеркалювальний коефіцієнт кореляції[ред. | ред. код]
Віддзеркалювальна кореляція (англ. reflective correlation) — це варіант пірсонової кореляції, в якому дані не центровано навколо їхніх середніх значень.[джерело?] Віддзеркалювальна кореляція сукупності це
Віддзеркалювальна кореляція симетрична, але не інваріантна щодо паралельного перенесення:
Віддзеркалювальна кореляція вибірки еквівалентна косинусній подібності:
Зважена версія вибіркової віддзеркалювальної кореляції це
Масштабний коефіцієнт кореляції[ред. | ред. код]
Масштабна кореляція (англ. scaled correlation) — це варіант кореляції Пірсона, в якому діапазон даних обмежують навмисно й контрольовано, щоби виявляти кореляції між швидкими складовими в часових рядах.[41] Масштабну кореляцію визначають як середню кореляцію над короткими сегментами даних.
Нехай це кількість сегментів, які можуть вміститися в загальну довжину сигналу для заданого масштабу :
Тоді масштабну кореляцію над усім сигналом обчислюють як
де — коефіцієнт кореляції Пірсона для сегмента .
Шляхом обирання параметра зменшують діапазон значень, і кореляції на довгих часових масштабах відфільтровуються, так, що виявляються лише кореляції на коротких часових масштабах. Таким чином усувають внески повільних складових і зберігають внески швидких складових.
Відстань Пірсона[ред. | ред. код]
Метрику відстані для двох змінних X та Y, відому як відстань Пірсона (англ. Pearson's distance), можливо визначати з коефіцієнта їхньої кореляції як[42]
Враховуючи те, що коефіцієнт кореляції Пірсона перебуває в межах [−1, +1], відстань Пірсона лежить на проміжку [0, 2]. Відстань Пірсона використовували в кластерному аналізі та виявлянні даних для передавання та зберігання з невідомими передавальним коефіцієнтом та зміщенням.[43]
Визначена таким чином «відстань» Пірсона для від'ємних кореляцій встановлює відстань понад 1. Насправді, значення мають як сильна додатна, так і сильна від'ємна кореляції, тому потрібно бути обережними при використанні «відстані» Пірсона в алгоритмах найближчих сусідів, оскільки такі алгоритми включатимуть лише сусідів із додатною кореляцією й виключати сусідів із від'ємною. Як альтернативу, можливо застосовувати відстань з абсолютним значенням, , яка враховуватиме як додатні, так і від'ємні кореляції. Інформацію про додатну та від'ємну пов'язаність можливо виділяти окремо пізніше.
Коловий коефіцієнт кореляції[ред. | ред. код]
Для змінних X = {x1,…,xn} та Y = {y1,…,yn}, визначених на одиничному колі , можливо визначити коловий (англ. circular) аналог коефіцієнта Пірсона.[44] Це робиться шляхом такого перетворення даних в X та Y за допомогою функції синуса, що коефіцієнт кореляції визначається як
де та — колові середні[en] X та Y. Ця міра може бути корисною в таких галузях як метеорологія, де важливий кутовий напрямок даних.
Частинна кореляція[ред. | ред. код]
Якщо сукупність або набір даних характеризується понад двома змінними, коефіцієнт частинної кореляції вимірює силу залежності між парою змінних, яка не пояснюється тим, як вони обидві змінюються у відповідь на варіації в обраній підмножині інших змінних.
Декореляція n випадкових змінних[ред. | ред. код]
Завжди можливо усунути кореляції між усіма парами довільного числа випадкових змінних за допомогою перетворення даних, навіть якщо взаємозв'язок між цими змінними нелінійний. Подання цього результату для розподілів сукупностей навели Кокс та Гінклі.[45]
Існує відповідний результат для зведення до нуля й вибіркових кореляцій. Припустімо, що вектор з n випадкових змінних спостерігають m разів. Нехай X — матриця, де — j-та змінна спостереження i. Нехай — квадратна матриця m на m з усіма елементами 1. Тоді D — це дані, перетворені так, що кожна випадкова змінна має нульове середнє, а T — це дані, перетворені так, що всі змінні мають нульове середнє й нульову кореляцію з усіма іншими змінними, — вибіркова кореляційна матриця T буде одиничною матрицею. Це потрібно додатково поділити на стандартне відхилення, щоб отримати одиничну дисперсію. Перетворені змінні будуть некорельованими, хоч вони й можуть бути не незалежними.
де степінь −1⁄2 подає квадратний корінь оберненої матриці. Матриця кореляції T буде одиничною. Якщо нове спостереження даних x це рядковий вектор з n елементів, то те саме перетворення можливо застосувати й до x, щоб отримати перетворені вектори d та t:
Декореляція пов'язана з аналізом головних компонент для багатовимірних даних.
Програмні втілення[ред. | ред. код]
- У базовому пакеті статистики R цей коефіцієнт кореляції втілено через
cor(x, y), або (з P-значенням) черезcor.test(x, y). - У бібліотеці Python SciPy — через
pearsonr(x, y). - Бібліотека Python Pandas втілює обчислення коефіцієнта кореляції Пірсона як варіант за замовчуванням для методу
pandas.DataFrame.corr - Wolfram Mathematica — через функцію
Correlation, або (з P-значенням) черезCorrelationTest. - Бібліотека C++ Boost — через функцію
correlation_coefficient. - Excel має вбудовану функцію
correl(array1, array2)для обчислення коефіцієнта кореляції Пірсона.
Див. також[ред. | ред. код]
- Відношення квадрантових кількостей[en]
- Відношення шансів[en]
- Дезатенюація[en]
- Квартет Анскомбе
- Коефіцієнт колігації[en]
- Коефіцієнт конкордації[en]
- Коефіцієнт кореляції рангу Спірмена
- Коефіцієнт множинної кореляції[en]
- Кореляційне відношення[en]
- Кореляція віддалі[en]
- Кореляція і залежність
- Максимальний інформаційний коефіцієнт[en]
- Множинна кореляція[en]
- Нормальна розподіленість і некорельованість не означає незалежність[en]
- Пов'язаність (статистика)
- Поліхорна кореляція[en]
- RV-коефіцієнт[en]
- Частинна кореляція
Виноски[ред. | ред. код]
- ↑ Відомий також як r Пі́рсона (англ. Pearson's r), коефіціє́нт кореля́ції моме́нту до́бутку Пі́рсона (англ. Pearson product-moment correlation coefficient, PPMCC), двови́мірна кореля́ція (англ. bivariate correlation)[1] та просто неконкретизований коефіціє́нт кореля́ції (англ. correlation coefficient)[2]
- ↑ Ще 1877 року Гальтон використовував термін «реверсія» (англ. "reversion", див. регресію до середнього) й символ «r» для того, що згодом стане «регресією» (англ. "regression").[3][4][5]
Примітки[ред. | ред. код]
- ↑ SPSS Tutorials: Pearson Correlation (англ.).
- ↑ Correlation Coefficient: Simple Definition, Formula, Easy Steps. Statistics How To (англ.).
- ↑ Galton, F. (5–19 April 1877). Typical laws of heredity. Nature (англ.). 15 (388, 389, 390): 492—495, 512—514, 532—533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. У додатку «Appendix» на сторінці 532 Гальтон використовує термін «reversion» та символ r.
- ↑ Galton, F. (24 September 1885). The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section. Nature (англ.). 32 (830): 507—510.
- ↑ Galton, F. (1886). Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute of Great Britain and Ireland (англ.). 15: 246—263. doi:10.2307/2841583. JSTOR 2841583.
- ↑ Pearson, Karl (20 June 1895). Notes on regression and inheritance in the case of two parents. Proceedings of the Royal Society of London (англ.). 58: 240—242. Bibcode:1895RSPS...58..240P.
- ↑ Stigler, Stephen M. (1989). Francis Galton's account of the invention of correlation. Statistical Science (англ.). 4 (2): 73—79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ↑ Analyse mathematique sur les probabilités des erreurs de situation d'un point. Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (фр.). 9: 255—332. 1844 — через Google Books.
- ↑ Wright, S. (1921). Correlation and causation. Journal of Agricultural Research (англ.). 20 (7): 557—585.
- ↑ а б в г д Real Statistics Using Excel, "Basic Concepts of Correlation" (англ.), отримано 22 лютого 2015 р.
- ↑ Weisstein, Eric W. Statistical Correlation. Wolfram MathWorld (англ.). Процитовано 22 серпня 2020.
- ↑ Moriya, N. (2008). Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes. У Yang, Fengshan (ред.). Progress in Applied Mathematical Modeling (англ.). Nova Science Publishers, Inc.[en]. с. 223–260. ISBN 978-1-60021-976-4.
- ↑ Garren, Steven T. (15 червня 1998). Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data. Statistics & Probability Letters (англ.). 38 (3): 281—288. doi:10.1016/S0167-7152(98)00035-2.
- ↑ 2.6 - (Pearson) Correlation Coefficient r. STAT 462 (англ.). Процитовано 10 липня 2021.
- ↑ Introductory Business Statistics: The Correlation Coefficient r. opentextbc.ca (англ.). Процитовано 21 серпня 2020.
- ↑ Rodgers; Nicewander (1988). Thirteen ways to look at the correlation coefficient (PDF). The American Statistician (англ.). 42 (1): 59—66. doi:10.2307/2685263. JSTOR 2685263.
- ↑ Schmid, John Jr. (грудень 1947). The relationship between the coefficient of correlation and the angle included between regression lines. The Journal of Educational Research (англ.). 41 (4): 311—313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ↑ Rummel, R.J. (1976). Understanding Correlation (англ.). гл. 5 (як проілюстровано для особливого випадку в наступному абзаці).
- ↑ Buda, Andrzej; Jarynowski, Andrzej (грудень 2010). Life Time of Correlations and its Applications (англ.). Wydawnictwo Niezależne. с. 5—21. ISBN 9788391527290.
- ↑ а б Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (англ.) (вид. 2nd).
- ↑ Bowley, A. L. (1928). The Standard Deviation of the Correlation Coefficient. Journal of the American Statistical Association (англ.). 23 (161): 31—34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ↑ Derivation of the standard error for Pearson's correlation coefficient. Cross Validated (англ.). Процитовано 30 липня 2021.
- ↑ Rahman, N. A. (1968) A Course in Theoretical Statistics (англ.), Charles Griffin and Company, 1968
- ↑ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship (англ.), Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ↑ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). On the distribution of the correlation coefficient in small samples. Appendix II to the papers of "Student" and R.A. Fisher. A co-operative study. Biometrika[en] (англ.). 11 (4): 328—413. doi:10.1093/biomet/11.4.328.
- ↑ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). Filtering induces correlation in fMRI resting state data. NeuroImage (англ.). 64: 728—740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ↑ Hotelling, Harold (1953). New Light on the Correlation Coefficient and its Transforms. Journal of the Royal Statistical Society. Series B (Methodological) (англ.). 15 (2): 193—232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ↑ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics (англ.). Т. Part 2 (вид. 2nd). Princeton, NJ: Van Nostrand.
- ↑ Weisstein, Eric W. Correlation Coefficient—Bivariate Normal Distribution. Wolfram MathWorld (англ.).
- ↑ Taraldsen, Gunnar (2020). Confidence in Correlation. ResearchGate (англ.). doi:10.13140/RG.2.2.23673.49769.
- ↑ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (січень 2019). A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty (PDF). Information Sciences (англ.). 470: 58—77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ↑ а б Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing (англ.). Academic Press.
- ↑ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). Robust estimation and outlier detection with correlation coefficients. Biometrika (англ.). 62 (3): 531—545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ↑ Huber, Peter. J. (2004). Robust Statistics (англ.). Wiley.[сторінка?]
- ↑ Vaart, A. W. van der (13 жовтня 1998). Asymptotic Statistics (англ.). Cambridge University Press. ISBN 978-0-511-80225-6.
- ↑ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. (англ.) ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ↑ Hotelling, H. (1953). New Light on the Correlation Coefficient and its Transforms. Journal of the Royal Statistical Society. Series B (Methodological) (англ.). 15 (2): 193—232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ↑ Olkin, Ingram; Pratt,John W. (March 1958). Unbiased Estimation of Certain Correlation Coefficients. The Annals of Mathematical Statistics (англ.). 29 (1): 201—211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ↑ Re: Compute a weighted correlation. sci.tech-archive.net (англ.).
- ↑ Weighted Correlation Matrix – File Exchange – MATLAB Central (англ.). Архів оригіналу за 15 травня 2021. Процитовано 14 січня 2024.
- ↑ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). Scaled correlation analysis: a better way to compute a cross-correlogram (PDF). European Journal of Neuroscience (англ.). 35 (5): 1—21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ↑ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (англ.) (pp. 110) ISBN 1-4020-8879-5
- ↑ Immink, K. Schouhamer; Weber, J. (жовтень 2010). Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch. IEEE Transactions on Information Theory (англ.). 60 (10): 5966—5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Процитовано 11 лютого 2018.
- ↑ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics (англ.). New Jersey: World Scientific. с. 176. ISBN 978-981-02-3778-3. Процитовано 21 вересня 2016.
- ↑ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics (англ.). Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
Посилання[ред. | ред. код]
- cocor. comparingcorrelations.org (англ.). — Безкоштовний вебінтерфейс та пакет R для статистичного порівняння двох залежних або незалежних кореляцій з перетинними або неперетинними змінними.
- Correlation. nagysandor.eu (англ.). — інтерактивна флешсимуляція кореляції двох нормально розподілених змінних.
- Correlation coefficient calculator. hackmath.net. Linear regression (англ.).
- Critical values for Pearson's correlation coefficient (PDF). frank.mtsu.edu/~dkfuller. — велика таблиця.
- Guess the Correlation (англ.). — Гра, в якій гравці вгадують, наскільки корельовані дві змінні на діаграмі розсіювання, щоби краще зрозуміти поняття кореляції.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|








![{\displaystyle \operatorname {cov} (X,Y)=\operatorname {\mathbb {E} } [(X-\mu _{X})(Y-\mu _{Y})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e88bc4ba085b98d5cca09b958ad378d50127308)

![{\displaystyle \rho _{X,Y}={\frac {\operatorname {\mathbb {E} } [(X-\mu _{X})(Y-\mu _{Y})]}{\sigma _{X}\sigma _{Y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042c646e848d2dc6e15d7b5c7a5b891941b2eab6)



![{\displaystyle {\begin{aligned}\mu _{X}={}&\operatorname {\mathbb {E} } [\,X\,]\\\mu _{Y}={}&\operatorname {\mathbb {E} } [\,Y\,]\\\sigma _{X}^{2}={}&\operatorname {\mathbb {E} } \left[\,\left(X-\operatorname {\mathbb {E} } [X]\right)^{2}\,\right]=\operatorname {\mathbb {E} } \left[\,X^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,X\,]\right)^{2}\\\sigma _{Y}^{2}={}&\operatorname {\mathbb {E} } \left[\,\left(Y-\operatorname {\mathbb {E} } [Y]\right)^{2}\,\right]=\operatorname {\mathbb {E} } \left[\,Y^{2}\,\right]-\left(\,\operatorname {\mathbb {E} } [\,Y\,]\right)^{2}\\&\operatorname {\mathbb {E} } [\,\left(X-\mu _{X}\right)\left(Y-\mu _{Y}\right)\,]=\operatorname {\mathbb {E} } [\,\left(X-\operatorname {\mathbb {E} } [\,X\,]\right)\left(Y-\operatorname {\mathbb {E} } [\,Y\,]\right)\,]=\operatorname {\mathbb {E} } [\,X\,Y\,]-\operatorname {\mathbb {E} } [\,X\,]\operatorname {\mathbb {E} } [\,Y\,]\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2469cdb397ef7d50c200b03c9e9f7311f0ab2b1)
![{\displaystyle \rho _{X,Y}={\frac {\operatorname {\mathbb {E} } [\,X\,Y\,]-\operatorname {\mathbb {E} } [\,X\,]\operatorname {\mathbb {E} } [\,Y\,]}{{\sqrt {\operatorname {\mathbb {E} } \left[\,X^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,X\,]\right)^{2}}}~{\sqrt {\operatorname {\mathbb {E} } \left[\,Y^{2}\,\right]-\left(\operatorname {\mathbb {E} } [\,Y\,]\right)^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5984dfb290912b0e0b92a984bf49cdd628c38b2c)










































![{\displaystyle z={\frac {x-{\text{середнє}}}{\text{SE}}}=[F(r)-F(\rho _{0})]{\sqrt {n-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/916cc8f541efd62b4f130e323b28937ddc720d37)

![{\displaystyle 100(1-\alpha )\%{\text{CI}}:\operatorname {arth} (\rho )\in [\operatorname {arth} (r)\pm z_{\alpha /2}{\text{SE}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8be13be9027658ed3f68b4e8fa53c068082be97)
![{\displaystyle 100(1-\alpha )\%{\text{CI}}:\rho \in [\operatorname {th} (\operatorname {arth} (r)-z_{\alpha /2}{\text{SE}}),\operatorname {th} (\operatorname {arth} (r)+z_{\alpha /2}{\text{SE}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/489f244f33868d5ba7821e92eacd44289c6f0b27)








![{\displaystyle {\begin{aligned}r(Y,{\hat {Y}})&={\frac {\sum _{i}(Y_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}(Y_{i}-{\hat {Y}}_{i}+{\hat {Y}}_{i}-{\bar {Y}})({\hat {Y}}_{i}-{\bar {Y}})}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}[(Y_{i}-{\hat {Y}}_{i})({\hat {Y}}_{i}-{\bar {Y}})+({\hat {Y}}_{i}-{\bar {Y}})^{2}]}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sqrt {\sum _{i}(Y_{i}-{\bar {Y}})^{2}\cdot \sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}}}\\[6pt]&={\sqrt {\frac {\sum _{i}({\hat {Y}}_{i}-{\bar {Y}})^{2}}{\sum _{i}(Y_{i}-{\bar {Y}})^{2}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86595f3f77e8ee96952760d9176a5fa140cc562)









![{\displaystyle \operatorname {\mathbb {E} } \left[r\right]=\rho -{\frac {\rho \left(1-\rho ^{2}\right)}{2n}}+\cdots ,\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/683b838e709e3b32a3c22dfec4fa665a593f42ad)




![{\displaystyle r=\operatorname {\mathbb {E} } [r]\approx r_{\text{adj}}-{\frac {r_{\text{adj}}\left(1-r_{\text{adj}}^{2}\right)}{2n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e094c3fdfcb0bfd127f4be74e582f22a407201c4)
![{\displaystyle r_{\text{adj}}\approx r\left[1+{\frac {1-r^{2}}{2n}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf3f71f2cfe17f8f0d422d5ac0d482cc429a925)




![{\displaystyle \operatorname {corr} _{r}(X,Y)={\frac {\operatorname {\mathbb {E} } [\,X\,Y\,]}{\sqrt {\operatorname {\mathbb {E} } [\,X^{2}\,]\cdot \operatorname {\mathbb {E} } [\,Y^{2}\,]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d897e4b303a062ed14cc9f88f35f5c8ffc91f7)





















