Історія тригонометрії
| Історія науки |
|---|
 Геодезичні вимірювання XVII сторіччя |
|
|
Історія тригонометрії як науки про співвідношення між кутами і сторонами трикутника та інших геометричних фігур охоплює понад два тисячоліття. Більшість таких співвідношень неможливо виразити за допомогою звичайних алгебричних операцій, тому знадобилось ввести особливі тригонометричні функції, які спершу оформлювали у вигляді таблиць.
Історики вважають, що тригонометрію створили стародавні астрономи, трохи пізніше її почали використовувати в геодезії й архітектурі. З часом сфера застосування тригонометрії постійно розширювалась, в теперішній час її використовують майже всі природничі науки, техніка і низка інших галузей діяльності[1]. Тригонометричні функції виявились особливо корисними для вивчення коливних процесів; на них заснований також гармонічний аналіз функцій та інші інструменти аналізу. Томас Пейн у своїй книзі «Доба Розуму» (1794) назвав тригонометрію «душею науки»[2].
Ранній період[ред. | ред. код]

Зародки тригонометрії можна знайти в математичних рукописах стародавнього Єгипту, Вавилона і стародавнього Китаю. 56-а задача з папірусу Рінда (II тисячоліття до н. е.) пропонує знайти нахил піраміди, висота якої дорівнює 250 ліктів, а довжина сторони основи — 360 ліктів[3].
Від вавилонської математики бере початок звичайне для нас вимірювання кутів градусами, мінутами і секундами (введення цих одиниць у давньогрецьку математику зазвичай приписують Гіпсиклу, II століття до н. е.) Серед теорем, відомих вавилонцям, була, приміром, така: вписаний кут, що спирається на діаметр кола — прямий[4]. Головним досягненням цього періоду стало співвідношення, яке згодом отримало назву теореми Піфагора; Ван дер Варден вважає, що вавилонці відкрили його між 2000 і 1786 роками до н. е.[5] Цілком можливо, що китайці відкрили його незалежно (див. «Математика в дев'яти книгах»). Незрозуміло, чи знали загальне формулювання теореми стародавні єгиптяни, однак прямокутний «єгипетський трикутник» зі сторонами 3, 4, і 5 був там добре відомий і широко використовувався.
Стародавня Греція[ред. | ред. код]
Загальне і логічно зв'язне викладення тригонометричних співвідношень з'явилося в давньогрецькій геометрії[6]. Грецькі математики ще не виділяли тригонометрію як окрему науку, для них вона буда частиною астрономії[7].
Плоска тригонометрія[ред. | ред. код]
Декілька теорем тригонометричного характеру містять «Начала» Евкліда (IV століття до н. е.). В першій книзі «Начал» теореми 18 і 19 встановлюють, що більшій стороні трикутника відповідає більший протилежний кут — і навпаки, більшому куту відповідає більша сторона. Теореми 20 і 22 формулюють «нерівність трикутника»: з трьох відрізків можна скласти трикутник тоді і тільки тоді, коли довжина кожного менше суми довжин двох інших. Теорема 32 доводить, що сума кутів трикутника дорівнює 180°.
У другій книзі «Начал» теорема 12 являє собою словесний аналог теореми косинусів[8]:
В тупокутних трикутниках квадрат на стороні, що стягує тупий кут, більше (суми) квадратів на сторонах, що містять тупий кут, на двічі взятий прямокутник, поміщений між однією зі сторін при тупому куті, на яку спадає перпендикуляр, і відрізком при тупому куті, який відтинає цей перпендикуляр ззовні.
Наступна теорема 13 є варіантом теореми косинусів для гострокутних трикутників. Аналогу теореми синусів у греків не було, це найважливіше відкриття було зроблене значно пізніше[9].

Подальший розвиток тригонометрії пов'язаний з ім'ям астронома Аристарха Самоського (III століття до н. е.). В його трактаті «Про величини і відстані Сонця і Місяця» була поставлена задача про визначення відстаней до небесних тіл; ця задача потребувала обчислення співвідношення сторін прямокутного трикутника при відомому значенні одного з кутів. Аристарх розглядав прямокутний трикутник, утворений Сонцем, Місяцем і Землею під час квадратури. Йому було потрібно обчислити величину гіпотенузи (відстань від Землі до Сонця) через катет (відстань від Землі до Місяця) при відомому значенні прилеглого кута (87°), що є еквівалентом обчислення значення . За оцінкою Аристарха, ця величина лежить у проміжку від 1/20 до 1/18, тобто відстань до сонця у 20 разів більше, ніж до Місяця[10]; насправді Сонце знаходиться майже у 400 разі далі, ніж Місяць, помилка виникла через неточність у вимірюванні кута. Водночас Аристарх довів нерівність, яка у сучасних термінах передається формулою:
Ця ж нерівність міститься в «Обчисленні піщинок» Архімеда[11]. В працях Архімеда (III століття до н. е.) наводиться важлива теорема ділення хорд, яка по суті еквівалентна формулі синуса половинного кута[12][13]:
Греки також вирішили проблему побудови трикутника за його трьома заданими елементами (з яких хоча б один є стороною)[6].
Протягом всього періоду розвитку античної науки головною нивою для застосування результатів плоскої тригонометрії у греків залишалась астрономія. Окрім задачі з обчислення відстаней, тригонометрію залучали для визначення параметрів системи епіциклів і/чи ексцентрів, якими представляли рух світила у просторі. За широко поширеною думкою, ця проблема вперше була сформульована Гіппархом (середина II століття до н. е.) при визначенні елементів орбіт Сонця і Місяця; можливо, аналогічними задачами займалися й астрономи більш раннього часу. Гіппарху також часто приписують авторство перших тригонометричних таблиць, які не збереглися[14]. Втім, згідно з деякими реконструкціями, перші тригонометричні таблиці були складені ще у III столітті до н. е., можливо, Апполонієм Перзьким[15].

Замість сучасної функції синуса Гіппарх та інші давньогрецькі математики звичайно розглядали залежність довжини хорди кола від заданого центрального кута (чи, що еквівалентно, від заданої дуги кола, вираженої у кутовій мірі). У сучасній термінології, довжина хорди, що стягує дугу θ одиничного кола дорівнює подвоєному синусу центрального кута θ/2. Ця відповідність справедлива для будь-яких кутів: 0° < θ < 360°. Мовою хорд були сформульовані перші відкриті греками тригонометричні співвідношення[1]. Наприклад, сучасній формулі:
у греків відповідала теорема[16]:
де — хорда для центрального кута , — діаметр кола.
При цьому радіус кола не вважався рівним одиниці, як тепер. Припускають, наприклад, що у Гіппарха радіус кола вважався рівним R=3438 одиниць — за такого визначення довжина дуги кола була рівною кутовій мірі цієї дуги, вираженої в мінутах: , і це полегшувало обчислення. У Птолемея R=60 одиниць. Згідно з сучасними реконструкціями[14] [17], величини хорд у Гіппарха були протабульовані з інтервалом 7°30'. Можливо, в основі обчислення таблиці Гіппарха лежав метод, що був розроблений Архімедом і брав початок ще у Аристарха[18].
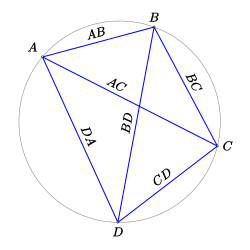
(теорема Птолемея)
Пізніше астроном II століття Клавдій Птолемей в «Альмагесті» доповнив результати Гіппарха. Тринадцять книг «Альмагеста» — найзначніша тригонометрична робота всієї античності. Зокрема, «Амальгест» містить великі п'ятизначні таблиці хорд для гострих і тупих кутів з кроком 30 кутових мінут[1]. Для обчислення хорд Птолемей використовував (у главі X) теорему Птолемея (втім, відому ще Архімеду), яка стверджує: сума добутків довжин протилежних сторін випуклого вписаного в коло чотирикутника дорівнює добутку довжин його діагоналей. З цієї теореми нескладно вивести дві формули для синуса і косинуса суми кутів і ще дві для синуса і косинуса різниці кутів, проте загальне формулювання цих теорем у греків відсутнє[19].
Основним досягненням античної тригонометричної теорії став розв'язок у загальному вигляді задачі «розв'язування трикутників», тобто заходження невідомих елементів трикутника, коли відомі його три елементи (з яких хоча б одним є стороною)[6]. Пізніше ця задача і її узагальнення стали основною задачею тригонометрії[1]: задані декілька (звичайно три) відомих елементи трикутника, вимагається знайти решту пов'язаних з ними величин. Спершу до числа елементів трикутника (відомих і невідомих) включали сторони і кути при їх вершинах, пізніше до них додались медіани, висоти, бісектриси, радіус вписаного і описаного кола, розташування центру ваги тощо. Прикладні тригонометричні задачі відрізняються великою різноманітністю — наприклад, можуть бути задані невидимі на практиці результаті дій над перерахованими величинами (приміром, сума кутів чи відношення довжин сторін).
Сферична тригонометрія[ред. | ред. код]
Паралельно з розвитком тригонометрії площини греки, під впливом астрономії, значно розвинули сферичну тригонометрію. В «Началах» Евкліда з цієї теми є тільки одна теорема про співвідношення об'ємів шарів різного діаметра, але потреби астрономії і картографії зумовили швидкий розвиток сферичної тригонометрії і суміжних з нею областей — системи небесних координат, теорії картографічних проєкцій, технології астрономічних приладів (зокрема, винайдено астролябію[20]).
Історики дійшли згоди щодо ступеню розвитку у античних греків геометрії небесної сфери. Деякі дослідники наводять аргументи, що екліптичну чи екваторіальну систему координат використовували для запису результатів астрономічних спостережень принаймні вже у час Гіппарха[21]. Можливо тоді були відомі і деякі теореми сферичної тригонометрії, які могли використовуватись для складення зоряних каталогів[22] і в геодезії.
Перші відомі в наш час праці зі «Сферики» (тобто сферичної геометрії, з очевидним астрономічним нахилом) написали[23]:
- (IV століття до н. е.) Автолік з Пітани і Евклід («Феномени»).
- (II століття до н. е.) Феодосій і Гіпсикл.
Деякі задачі розглянуті в цих творах мають тригонометричний характер, проте через слабку розробленість теорії автори ще користуються обхідними шляхами. Наприклад, задачу «знайти час повного сходу (заходу) зодіакального сузір'я» Гіпсикл вирішує наближено за допомогою многокутних чисел[23].

Вирішальним етапом в розвитку теорії стала монографія «Сферика» в трьох книгах, яку написав Менелай Александрійський (близько 100 року н. е.). В першій книзі він виклав теореми про сферичні трикутники, аналогічні теоремам Евкліда про плоскі трикутники (див. I книгу «Начал»). Історики вважають, що підхід Менелая багато в чому спирається на праці Феодосія, які у Менелая суттєво розширені і зведені в систему. Як повідомляє Паппа, Менелай першим ввів поняття сферичного трикутника як фігури, утвореної відрізками великих кіл[24]. Менелай довів теорему, для якої у Евкліда немає плоского аналога: два сферичних трикутники конгруентні (сумісні), якщо відповідні кути рівні. Інша його теорема стверджує, що сума кутів сферичного трикутника завжди більше 180°[24].
Друга книга «Сферики» викладає застосовування сферичної тригонометрії до астрономії. Третя книга місить важливу для практичної астрономії теорему Менелая, відому як «правило шести величин»[25]. Дві інші відкриті Менелаєм фундаментальні теореми пізніше отримали назви «правило чотирьох величин» і «правило тангенсів»[24].
Кілька десятиліть потому Клавдій Птолемей у своїх працях «Географія», «Аналемма» і «Планісферій» приводить докладне викладення застосування тригонометрії до картографії, астрономії і механіки. Серед іншого, описана стереографічна проєкція, досліджені кілька практичних задач, наприклад: визначити висоту і азимут небесного світила за його схиленням і часовим кутом. З точки зору тригонометрії, це означає, що потрібно знайти сторону сферичного трикутника за двома іншими сторонами і протилежним кутом[26].
Сферичній геометрії Птолемей також присвятив XIII главу в першій книзі «Амельгеста»; на відміну від Менелая, Птолемей не привів доведень багатьох тверджень, але натомість приділив багато уваги алгоритмам, придатним для практичних обчислень в астрономії. Опорною конструкцією в «Амальгесті» слугує, замість плоских хорд, «чотиристоронник Менелая». Для вирішення прямокутного сферичного трикутника, тобто для обчислення його характеристик, Птолемей навів у словесній формі 4 теореми; в сучасних позначеннях вони мають вигляд (кут прямий)[27]:
- (окремий випадок сферичної теореми синусів)
- (окремий випадок сферичної теореми синусів)
Пояснимо, що в сферичній геометрії прийнято вимірювати сторони трикутника не лінійними одиницями, а величиною центральних кутів, що на них спираються. В сучасній сферичній геометрії наводяться ще два співвідношення:
- (також виходить з сферичної теореми косинусів)
У Птолемея вони відсутні, оскільки їх неможливо вивести з теореми Менелая[27].
Середньовіччя[ред. | ред. код]
Індія[ред. | ред. код]
У IV столітті, після занепаду античної науки, центр розвитку математики змістився до Індії. Твори індійських математиків (сіддханти) демонструють, що їх автори були добре знайомі з працями грецьких астрономів і геометрів[28]. Чистою геометрією індійці цікавились мало, але їх внесок в прикладну астрономію і розрахункові аспекти тригонометрії дуже значний.

В першу чергу індійці змінили деякі концепції тригонометрії, наблизивши їх до сучасних. Вони провели заміну античних хорд на синуси (назва синус походить від слова тятива на санскриті[29]) в прямокутному трикутнику. Тим самим в Індії була започаткована тригонометрія як загальне вчення про співвідношення у трикутнику, хоча, на відміну від грецьких хорд, індійський підхід обмежувався тільки функціями гострого кута[30].
Синус індійці визначали інакше, ніж в сучасній математиці (див. мал. праворуч): під синусом розуміли довжину відрізку AD, що спирався на дугу AC кола з радіусом R=3438 одиниць (як у Гіппарха). Таким чином, «індійський синус» кута у 3438 разів більше сучасного синуса і мав розмірність довжини[29]. З цього правила були винятки: наприклад, Брамагупта з неясних причин узяв радіус рівний 3270 одиниць[31].
Індійці першими ввели у використання косинус. Використовувався ще так званий обернений синус, чи синус-верзус, рівний довжині відрізку DC на малюнку праворуч[32].
Як у греків, тригонометрія індійців розвивалася головним чином у зв'язку з її астрономічним застосуванням, в основному для використання в теорії руху планет і для вивчення небесної сфери. Це свідчить про добре знання сферичної тригонометрії «Амальгеста» і «Аналемми», однак жодної їх власної роботи, яка б розвивала теорію цього розділу тригонометрії, не виявлено[33]. Тим не менш в розробленні прикладних алгоритмів вирішення астрономічних задач індійці досягнули великих успіхів[28]. Наприклад, в «Панча-сіддхантиці» Варахаміхіри (VII століття) наводиться оригінальне вирішення астрономічної задачі, описаної у Птолемея: знайти висоту сонця над горизонтом, якщо відомі широта місцевості, схилення Сонця і його часовий кут. Для вирішення автор застосовує аналог теореми косинусів[34], він також вперше навів формулу для синуса половинного кута[35].

Для астрономічних розрахунків був складений ряд тригонометричних таблиць. Перші (чотиризначні) таблиці синусів наведені в стародавній «Сурья-сіддханті» і у Аріабхати («Аріабхатія», V століття). Таблиці Аріабхати містять 24 значення синусів і синус-верзусів з інтервалом 3°45' (половина кроку таблиць у Гіппарха).
Важливий внесок в розвиток тригонометрії зробив Брахмагупта (VII століття), який відкрив декілька тригонометричних співвідношень, зокрема й ті, що в сучасному запису набули вигляду[34]:
Крім того, індійці знали формули для кратних кутів , для . В «Сурья-сіддханті» і в працях Брахмагупти при вирішенні задач фактично використовується сферичний варіант теореми синусів, однак загальне формулювання цієї теореми в Індії так і не з'явилось[36]. Історики виявили в індійських працях неявне використання тангенсів, але важливість цього поняття була усвідомлена тільки пізніше, математиками ісламських країн[28].
В працях іншого видатного ученого, Бхаскари II (XII століття), наведені формули для синуса і косинуса суми і різниці кутів:
а також формула для малого приросту синуса:
(при ), відповідна сучасному виразу для диференціалу синуса. Спираючись на формулу синуса суми, Бхаскара опублікував більш точні і докладні, ніж у Аріабзати, тригонометричні таблиці з кроком 1°[37].
У XI столітті мусульмани (Махмуд Газневі) захопили і спустошили Північну Індію. Культурні центри перемістилися до Південної Індії, де сформувалася так звана школа «Керала» (за назвою сучасного штату Керала на півдні Індії)[38]. У XV—XVI століттях математики Керали під час астрономічних досліджень досягли великих успіхів в області сумування нескінченних числових рядів, в тому числі для тригонометричних функцій[36]. В анонімному трактаті «Каранападдхаті» («Техніка обчислення») наведені правила розкладання синуса і косинуса на нескінченні степеневі ряди[39], що імовірно брали початок від засновника цієї школи астронома Мадхава (1 пол. XV століття)[40]. Мадхава і його послідовник Нілаканта (у трактаті «Тантрасанраха») наводять також правила розкладання арктангенса в нескінечнний степеневий ряд. В Європі до подібних результатів дійшли лише у XVII—XVIII століттях. Так, ряди для синуса і косинуса вивів Ісаак Ньютон близько 1666 року, а ряд арктангенса був знайдений Дж. Грегорі у 1671 році і Ґ. В. Лейбніцем у 1673 році[41].
Ісламські країни[ред. | ред. код]
У VIII столітті учені країн Близького і Середнього Сходу познайомилися з працями давньогрецьких та індійських математиків і астрономів. Їх перекладом арабською мовою займалися такі видатні учені VIII століття, як Ібрахім аль-Фазарі і Якуб ібн Тарік. Надалі вони та їх послідовники почали активно коментувати і розвивати ці теорії. Опорною конструкцією у ісламських учених, як і у індійців, були синус в трикутнику, чи, що є тим самим, напівхорда у колі[33].
Їх астрономічні трактати, аналогічні індійським сіддхантам, мали назву «Зідж». Типовий зідж являв собою збірку астрономічних і тригонометричних таблиць у супроводі керівництва з їх застосування і (не завжди) викладення загальної теорії[42]. Порівняння зіджів періоду VIII—XIII століть демонструє швидку еволюцію тригонометричних знань. Предметом особливої уваги учених ісламських країн була сферична тригонометрія, методи якої використовувались для вирішення задач астрономії і геодезії[43]. Серед основних проблем, що вирішувалися, були наступні[44][42]:
Точне визначення часу доби.
- Обчислення майбутнього розташування небесних світил, моментів їх сходу і заходу, затемнень Сонця і Місяця.
- Знаходження географічних координат поточного місця.
- Обчислення відстані між містами з відомими географічними координатами.
- Визначення напряму на Мекку (кібла) з заданого місця.

Серед праць, що збереглися, найбільш ранні належать аль-Хорезмі та аль-Марвазі (IX століття), які розглянули, разом з відомими це індійцям синусом і косинусом, нові тригонометричні функції: тангенс, котангенс, секанс і косеканс[32]. Спершу ці функції визначались інакше, між у сучасній математиці. Так, під котангенсом розуміли довжину тіні від вертального гномона висотою 12 (іноді 7) одиниць; спочатку ці поняття використовувались для розрахунку сонячних годин. Тангенсом називали тінь від горизонтального гномона. Косекансом і секансом називали гіпотенузи відповідних прямокутних трикутників (відрізки АО на малюнку праворуч)[45]. Лише у X столітті філософ і математик аль-Фарабі в своїх коментарях до «Альмагеста» ввів незалежні від гномоніки визначення цих чотирьох функцій, визначивши їх через синус і косинус в тригонометричному колі з птолемеївським радіусом (60 одиниць). Основні співвідношення між всіма шістьма функціями навів аль-Баттані у тому ж сторіччі. Кінцевої уніфікації домігся Абу-л-Вафа у другій половині X століття, який вперше використав для визначення тригонометричних функцій коло з одиничним радіусом, як це робиться у сучасній математиці.
Сабіт ібн Курра (IX століття) і аль-Баттані (X століття) першими відкрили фундаментальну теорему синусів для окремого випадку прямокутного сферичного трикутника. Для довільного сферичного трикутника доведення було знайдене (різними способами, і, ймовірно, незалежно одне від одного) Абу-л-Вафою, аль-Ходжанді й ібн Іраком наприкінці X століття[46]. В іншому трактаті ібн Ірака сформульована і доведена теорема синусів для плоского трикутника[47].
Сферична теорема косинусів у загальному вигляді не була сформульована в країнах ісламу, однак у працях Сабіта ібн Курри, аль-Баттані та ніших астрономів наявні твердження їй еквівалентні. Імовірно, тому Регіомонтан, який вперше запропонував загальне формулювання цього важливого співвідношення (XV століття), дав йому назву «теорема Альбатегнія» (так тоді в Європі називали аль-Баттані)[48].
Ібн Юніс (X століття) відкрив перетворення добутку тригонометричних функцій на суму[49], наприклад:
Формули перетворень дозволяли замінити трудомістке множення на простіше додавання і віднімання. пізніше в Європі ці є формули використовували з протилежною метою — для заміни додавання і віднімання на множення, для того, щоб потів для обчислення результату застосувати логарифмічні таблиці[50].
Одним з важливіших завдань науки тих часів було складення тригонометричних таблиць з якнайменшим кроком. У IX столітті аль-Хорезмі склав таблиці синусів з кроком 1°, його сучасник аль-Марвазі додав до них перші таблиці тангенсів, котангенсів і косекансів (з тим самим кроком)[32]. На початку X століття аль-Баттані опублікував таблиці з кроком 30', наприкінці того ж століття Ібн Юніс склав таблиці з кроком 1'[51]. При складанні таблиць ключовим питанням було обчислення значення . Майстерні методі для обчислення цієї величини винайшли Ібн Юніс, Абу-л-Вафа, аль-Біруні. Найбільшого успіху домігся у XV століття іль-Каши; в одній зі своїх праць він підрахував, що (всі знаки є вірними). У складених за його участі «Астрономічних таблицях» Самаркандської обсерваторії Углубека таблиці синусів обчислені з шістьма шістдесятковими знаками[52], з кроком 1'. Султан Угулбек особисто брав участь в цій роботі: він написав спеціальний трактат про обчислення синуса кута в 1°.
Першим спеціалізованим трактатом з тригонометрії був твір середньоазійського ученого аль-Біруні (X—XI століття) «Книга ключів науки астрономії» (995—996 роки). Цілий курс тригонометрії містив головну працю алі-Біруні — «Канон Мас‘уда» (книга III). На додаток до таблиць синусів (з кроком 15') Ал-Бируні навів таблиці тангенсів (з кроком 1°). Ідеологічно праці Біруні близькі до птолемеєвських — мовою хорд він формулює теореми про синус подвоєного і половинного кута, синус суми і різність кутів[53]. Серед додатків книги аль-Біруні показує побудову правильного вписаного дев'ятикутника і наближене обчислення довжини його сторони; цей алгоритм він використовує для знаходження . В іншій праці, «Геодезія», Біруні навів результати власних вимірювань довжини земного меридіану, слідством з яких є оцінка радіуса Землі, близька до істинної (в перерахунку у метричну систему, Біруні отримав 6340 км)[54].
Фундаментальне викладення тригонометрії як самостійної науки (як плоскої, так і сферичної) навів перський математик і астроном Насир ад-Дін ат-Тусі у 1260 році[55]. Його «Трактат про повний чотиристоронник» містить практичні способи вирішення типових задач, в тому числі найскладніших, вирішених самим ат-Тусі — приміром, побудова сторін сферичного трикутника за трьома заданими кутами[56]. Наведена теорема тангенсів для сферичних трикутників, описане важливе поняття полярного трикутника (вперше використане у XI столітті Ібн Іраком і аль-Джайяні). Твір ат-Тусі став широковідомим в Європі й здійснив істотний вплив на розвиток тригонометрії.
Таким чином, до кінця XIII століття були відкриті базові теореми, що складають зміст тригонометрії:
- Вираження будь-якої тригонометричної функції через будь-яку іншу.
- Формули для синусів і косинусів кратних і половинних кутів, а також для суми і різниці кутів.
- Теореми синусів і косинусів.
- Вирішення плоских і сферичних трикутників.
Через відсутність алгебричної символіки всі перераховані теореми виражались у громіздкій словесній формі, але по суті були повністю еквівалентними їх сучасному розумінню.
Європа[ред. | ред. код]

Після того, як арабські трактати були в XII—XIII століттях перекладені на латину, багато ідей індійських і перських математиків стали надбанням європейської науки. Скоріш за все, перше знайомство європейців з тригонометрією відбулось завдяки зіджу аль-Хорезмі, два переклади якого були виконані у XII столітті. Спершу відомості про тригонометрію (правила її використання, таблиці деяких тригонометричних функцій) наводились у творах з астрономії, однак у творі Фібоначчі «Практика геометрії», написаному близько 1200 року, тригонометрія викладається як частина геометрії. Першим європейських твором, цілком присвяченим астрономії, часто називають «Чотири трактати про прямі й обернені хорди» англійського астронома Річарда Воллінгфордського (близько 1320 р.). Книга містить доведення низки тригонометричних тотожностей і оригінальний метод обчислення синусів. Приблизно у ті ж роки був написаний трактат європейського математика Леві бен Гершома «Про синуси, хорди і дуги», перекладений на латинську мову 1324 року[57]. Книга містить доведення теореми синусів і п'ятизначні таблиці синусів[58]. Тригонометрії торкається «Теоретична геометрія» англійського математика Томаса Брадвардіна (написана у першій половині XIV ст., опублікована у 1495 році). Тригонометричні таблиці, частіше перекладені з арабської, але іноді оригінальні, містяться у працях низки інших авторів XIV—XV століть. Тоді ж тригонометрія обійняла своє місце серед університетських курсів.
Великим досягненням стала монографія Регіомонтана «П'ять книг про трикутники всіх сидів» (опублікована у 1462—1464), в якій були зведені все відомі до цього моменту знання з плоскої та сферичної тригонометрії і прикладені семизначні таблиці синусів (з кроком 1') і тангенсів (з кроком 1'). Суттєво й те, що в таблицях Регімонтана, порушуючи астрономічну традицію, вперше використовувалась десяткова система (а не архаїчна шістедисяткова). Радіус тригонометричного кола Регіомонтан прийняв рівним , щоб табличні значення були представлені цілими числами (десяткові дроби ввійшли у вжиток дещо пізніше, причому потужним стимулом до їх застосування стали саме тригонометричні обчислення[59]).
У порівнянні з трактатом ат-Тусі праця Регіомонтана є істотно повнішою, вона містить низку нових задач, вирішених оригінальними методами. Наприклад, показується як побудувати трикутник, якщо відома його сторона, довжина спадаючої на неї висоти і протилежний кут[60].
Новий час[ред. | ред. код]

XVI—XVII століття[ред. | ред. код]
Розвиток тригонометрії у Новий час став надзвичайно важливим не тільки для астрономії та астрології, але й для інших галузей, в першу чергу артилерії, оптики і навігації у далеких морських подорожах. Тому після XVI століття цією темою займалися багато видатних вчених, в тому числі Миколай Коперник, Йоганн Кеплер, Франсуа Вієт[61]. Коперник присвятив тригонометрії дві глави у своєму трактаті «Про обертання небесних сфер» (1543). Незабаром (1551) з'явились 15-значні тригонометричні таблиці Ретика, учня Коперника, з кроком 10"[62]. Кеплер опублікував працю «Оптична частина астрономії» (1604).
Потреба у складних тригонометричних розрахунках викликала на початку XVII століття відкриття логарифмів, причому перші логарифмічні таблиці Джона Непера містили тільки логарифми тригонометричних функцій. Серед інших відкриттів Непера — ефективний аглоритм розв'язання сферичних трикутників, що отримав назву «формули аналогії Непера»[63].
Термін «тригонометрія» як назву математичної дисципліни вів в обіг німецький математик Б. Пітискус[en], який облікував у 1595 році книгу «Тригонометрія, або стислий і ясний трактат про розв'язування трикутників» (лат. Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuous). До кінця XVII століття з'явились сучасні назви тригонометричних функцій. Термін синус вперше застосував близько 1145 року англійський математик і арабіст Роберт Честерський[en][29]. Регімонтан у своїй книзі назвав косинус «синусом доповнення» (лат. sinus complementi), оскільки ; його послідовники у XVII столітті скоротили це позначення до co-sinus (Едмунд Гунтер)[61], а пізніше — до cos (Вільям Отред). Назви тангенса і секанса запропонував у 1583 році данський математик Томас Фінке (Thomas Fincke)[61]. в згаданий вище Едмунд Гунтер ввів назви котангенса і косеканса. Термін «тригонометричні функції» вперше застосував у своїй «Аналітичній тригонометрії» (1770) Георг Симон Клюгель[64].

Томас Фінке запропонував оригінальне вирішення геодезичної задачі: знайти кути трикутника, якщо відома їх сума і співвідношення протилежних сторін . Для вирішення Фінке використав формулу Регіомонтана (див. малюнок)[65]:
Вієт у першій частині свого «Математичного канону» (1579) помістив різноманітні таблиці, зокрема тригонометричні, а в другій частині навів ґрунтовні і систематичні, хоча й без доказів, викладення плоскої і сферичної тригонометрії. У 1593 році Вієт підготував розширене видання цієї праці, відзначають, що його інтерес до алгебри спершу був викликаний можливістю застосування до тригонометрії та астрономії[66]. Другим важливим здобутків Вієта було застосування в тригонометрії розробленої ним загальної алгебричної символіки; якщо раніше вирішення задачі розумілось як геометрична побудова, то починаючи з робіт Вієта пріоритет почав переходити до алгебричних обчислень[67]. поява символіки дозволила записати у компактному і загальному вигляді тригонометричні тотожності — наприклад, формули кратних кутів[68]:
Потрібно зазначити, що сам Вієт подав ці формули ще частково у словесному описі, але при цьому ясно вказав на зв'язок коефіцієнтів формул з біномінальними коефіцієнтами і навів таблицю їх значень для невеликих значень [66].
Серед інших досягнень Вієта[69]: в праці «Доповнення до геометрії» Вієт вказав тригонометричний спосіб вирішення кубічного рівняння для найскладнішого в той період — незвідного — випадку (стандартна формула вимагає вміння працювати з коренями з комплексних чисел). Вієт навів перший в історії нескінченний добуток:

Окрім артилерії і навігації, тригонометрія розвивалась швидкими темпами і в таких класичних сферах її застосування, як геодезія. Широке застосування тангенсів пояснювалось, зокрема, простотою вимірювання за їх допомогою висоти гори чи будівлі (див. малюнок):
У 1615 році Снелліус знайшов вирішення «задачі Снелліуса-Потно»[en]: знайти точку, з якої сторони даного (плоского) трикутника видно під заданими кутами. Він відкрив закон закон заломлення світла: для заданих початкового середовища і середовища заломлення співвідношення синусів кута падіння і кута заломлення є постійним. Цим Снелліус відкрив дорогу новим застосуванням тригонометричних функцій в оптиці, а винайдення в ті ж роки перших телескопів надало цьому відкриттю особливої важливості.
У 1630-х роках Жиль Роберваль, під час своїх досліджень циклоїди, накреслив перший графік синусоїди[70]. Також він опублікував формулу тангенса подвійного кута[50]. Джон Валліс у своїй «Механіці» (1670), випередивши свій час, вірно вказав знаки синуса у всіх квадрантах і вказав, що у синусоїди нескінченно багато обертів. Графік тангенса для першого квадранта вперше накреслив Джеймс Грегорі (1668)[71].
У другій половині XVII століття почався стрімкий розвиток загальної теорії квадратур (тобто обчислення площі), який завершився появою в кінці сторіччя математичного аналізу. Для тригонометричних функцій важливі результати на початку цього періоду отримав Блез Паскаль (опубліковані в його книзі «Листи А. Деттонвілля про деякі його геометричні відкриття», 1659 рік). У сучасній термінології, паскаль обчислив інтеграли від натуральних степенів синуса і косинуса і деякі пов'язані з ними[72], а також відзначив, що . Роботи в сфері тригонометрії проводили такі великі математики XVII століття, як Отред, Гюйгенс, Озанам, Валліс. Помітним процесом у другій половині XVII століття стала поступова алгебризація тригонометрії, удосконалення і срощення її символіки (хоча до Ейлера символіка була все ж набагато більш громіздкою, ніж сучасна)[73].
XVIII століття[ред. | ред. код]
Після відкриття математичного аналізу спершу Джеймс Грегорі, а потім Ісаак Ньютон отримали розкладання тригонометричних функцій (а також обернених до них) у нескінченні ряди. Ньютон присвятив проблемам геометрії і тригонометрії 10 задач у своїй книзі «Універсальна арифметика»[74]. Наприклад, в задачі X потрібно «розв'язати трикутник», якщо відомі одна його сторона, протилежний кут і сума двох інших сторін. Запропонований Ньютоном метод вирішення являє собою одну з його формул Мольвейде[75].
Лейбніц строго довів, що не може буди, власне, алгебраїчно виражений через , тобто за сучасною термінологією, тригонометричні функції трансцендентні[76].
Важливими відкриттями на початку XVIII століття стали:
- Відкриття і широке поширення радіанної міри кутів[77] (Роджер Котс, 1714). Сам термін «радіан» з'явився пізніше, його у 1873 році запропонував англійський інженер Джеймс Томсон[78].
- Тригонометричні уявлення комплексного числа і формула Муавра.
- Початок використання (Ньютон і Грегорі) полярної системи координат, пов'язаної з декартовою тригонометричними співвідношеннями; у загальний обіг ці координати ввів Ейлер (1748)[79].
У 1706 році швейцарський математик Якоб Герман опублікував формули для тангенса суми і тангенса кратних кутів, Йоганн Ламберт у 1765 році знайшов надзвичайно корисні формули, що виражають різні тригонометричні функції через тангенс половинного кута[80]. Досліджуючи гіперболічні функції (1761), Ламберт показав, що їх властивості аналогічні властивостям тригонометричних; причину цього ще у 1707 році виявив Муавр: при заміні дійсного аргументу на уявний коло переходить в гіперболу, а тригонометричні функції — у відповідні гіперболічні[81].
Німецький математик Фрідрих Вільгельм фон Оппель в книзі «Аналіз трикутників» (1746) опублікував у сучасному записі обидві формули Мольвейде[82].
Реформи Леонарда Ейлера[ред. | ред. код]

Сучасного вигляду тригонометрії надав Леонард Ейлер. В трактаті «Введення в аналіз нескінченних» (1748) Ейлер навів визначення тригонометричних функцій, еквівалентне сучасному[74], і відповідно визначив обернені функції. Якщо його попередники розуміли синус та інші поняття геометрично, тобто як лінії в колі чи трикутнику, то після робіт Ейлера , , тощо стали розглядатися як безрозмірні аналітичні функції дійсного і комплексного змінного. Для комплексного випадку він встановив зв'язок тригонометричних функцій з показниковою функцією (формула Ейлера). Підхід Ейлера з тих пір став загальновизнаним і увійшов до підручників.
Ейлер розглядав як допустимі від'ємні кути і кути більше 360°, що дозволило визначити тригонометричні функції на всій дійсній числовій прямій, а потім продовжити їх на комплексну площину. Коли постало питання про поширення тригонометричних функцій на тупі кути, знаки цих функцій до Ейлера часто обирались помилково; багато математиків вважали, наприклад, косинус і тангенс тупого кута додатними[70]. Ейлер визначив ці знаки для кутів у різних координатних квадрантах, виходячи з формул зведення[83].
Ейлер вперше навів розкладання тригонометричних функцій у нескінченні добутки (1734), звідки вивів ряди для їх логарифмів[84].
В інших працях, в першу чергу «Основи сферичної тригонометрії, виведені з метода максимумів і мінімумів» (1753) і «Загальна сферична тригонометрія, коротко та ясно виведена з перших основ» (1779), Ейлер вперше навів повне систематичне викладення сферичної тригонометрії на аналітичних засадах[85], причому багато зі великих результатів належать самому Ейлеру.
В середині XVIII століття розгорівся найважливіший за наслідками «спір про струну»[86]. Эйлер в полеміці з д'Аламбером запропонував більш загальне визначення функції, ніж приймалося раніше; зокрема, функція може бути задана тригонометричним рядом. В своїх працях Ейлер використовував декілька подань алгебричних функцій у вигляді ряду з кратних аргументів тригонометричних функцій, наприклад[87]:
Загальною теорією тригонометричних рядів Ейлер не займався і збіжність отриманих результатів не досліджував, але отримав декілька важливих результатів. Зокрема, він вивів розклади цілих степенів синуса і косинуса[87]>.
XIX—XXI століття[ред. | ред. код]
На початку XIX століття М. І. Лобачевський додав до плоскої і сферичної тригонометрії третій розділ — гіперболічну (для геометрії Лобачевського, першу роботу в цій галузі опублікував Ф. А. Таурінус у 1826 році). Лобачевський показав, що формули сферичної тригонометрії переходять у формули гіперболічної тригонометрії при заміні довжин сторін трикутника a, b, c на уявні величини: ai, bi, ci — чи, що еквівалентно, при заміні тригонометричних функцій на відповідні гіперболічні[88].
У XIX—XX століттях стрімкого розвитку набули теорія тригонометричних рядів і пов'язані з нею області математики: гармонічний аналіз, теорія випадкових процесів, кодування аудіо і відеоінформації та інші. Ще Даниїл Бернуллі висловив думку, що будь-яку (неперервну) функцію на заданому проміжку можна представити тригонометричним рядом[89]. Дискусії тривали до 1807 року, коли Фур'є опублікував теорію представлення довільних шматково-аналітичних функцій тригонометричними рядами (кінцевий варіант міститься в його «Аналітичній теорії тепла», 1822)[90]. Для розкладання функції в ряд:
Фур'є навів інтегральні формули розрахунку коефіцієнтів[90]:
Виклад Фур'є не був строгим у сучасному розумінні, але вже містив дослідження збіжності більшості отриманих ним рядів. Для функцій, заданих на всій числовій прямій і функцій, які не є періодичними, Фур'є запропонував розкладання в інтеграл Фур'є.
Універсальність та ефективність методів аналізу Фур'є справили великий вплив на науковий світ. Якщо раніше тригонометричні ряди використовувались в математичній фізиці переважно для вивчення періодичних процесів (коливання струни, небесна механіка, рух маятника тощо), то в праці Фур'є досліджувались процеси зовсім іншого порядку (теплопередача), і тригонометричні ряди допомогли отримати цінні практичні результати. З того моменту тригонометричні ряди та інтеграли стали потужним інструментом аналізу різноманітних функцій. Результати Фур'є розвинули і поглибили Пуассон і Коші, питання збіжності рядів ретельно досліджували Діріхле та інші математики[91]. Ріман у своїй дисертації досліджував довільні тригонометричні ряди, не обов'язково пов'язані з розкладанням якої-небудь функції (1853), сформулював для них «принцип локалізації». Питання про зображуваність вимірної і скінченної майже крізь функції тригонометричним рядом (який не обов'язково збігається з її рядом Фур'є) було вирішене у 1941 році теоремою Меньшова.
Досліджуючи множини особливих точок для тригонометричних рядів, Георг Кантор розробив фундаментальну для всієї математики теорію множин[92]. Величезний вплив теорія тригонометричних рядів справила на розвиток комплексного аналізу, математичної фізики, електроніки і багатьох інших розділів науки[90]. Теорія функцій дійсного змінного, теорія міри та інтеграл Лебега з'явились і надалі розвивались у тісному зв'язку з теорією геометричних рядів[90][93]. Важливі практичні застосування має наближення функцій скінченими тригонометричними поліномами[94] (яке використовується також для інтерполювання).
Історики тригонометрії[ред. | ред. код]
У XVIII—XIX століттях праці з історії математики і астрономії значну увагу приділяли й історії тригонометрії (Ж. Е. Монтукла, Ж. Б. Ж. Деламбр, Г. Ганкель, П. Таннері та інші). У 1900 році німецький історик математики Антон фон Браунмюль опублікував першу монографію (у двох томах), спеціально присвячену історії тригонометрії[95]. У XX столітті значні роботи з цієї теми опублікували І. Г. Цейтен, М. Б. Кантор, О. Нейгебауер[ru], Б. А. Розенфельд[ru], Г. П. Матвієвська та інші.
Примітки[ред. | ред. код]
- ↑ а б в г Справочник по элементарной математике. — М. : Наука, 1978. — С. 266-268.
- ↑ Paine, Thomas. The Age of Reason. — Dover Publications, 2004. — С. 52.
- ↑ Eli Maor. Trigonometric Delights. — Princeton University Press, 1998. — P. 20. — ISBN 0-691-09541-8.
- ↑ Глейзер Г. И., 1982, с. 95..
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
- ↑ а б в Глейзер Г. И., 1982, с. 77.
- ↑ Цейтен Г. Г., 1938, с. 124-125.
- ↑ Глейзер Г. И., 1982, с. 94-95..
- ↑ Матвиевская Г. П., 2012, с. 92-96.
- ↑ Цейтен Г. Г., 1932, с. 153-154..
- ↑ Веселовский, 1961, с. 38.
- ↑ Матвиевская Г. П., 2012, с. 15..
- ↑ Boyer, Carl B. A History of Mathematics. — Second ed. — John Wiley & Sons, Inc, 1991. — P. 158–159. — ISBN 0-471-54397-7.
- ↑ а б Toomer, 1973.
- ↑ Van der Waerden, 1988.
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 77..
- ↑ Thurston, 1994.
- ↑ Duke, 2011.
- ↑ Хрестоматия по истории математики, 1976, с. 195-197..
- ↑ Матвиевская Г. П., 2012, с. 25-27.
- ↑ Duke, 2002.
- ↑ Sidoli, 2004.
- ↑ а б Матвиевская Г. П., 2012, с. 27-33.
- ↑ а б в Матвиевская Г. П., 2012, с. 33-36.
- ↑ История математики, том I, 1970, с. 141-142.
- ↑ Цейтен Г. Г., 1932, с. 158-162.
- ↑ а б Матвиевская Г. П., 2012, с. 36-39.
- ↑ а б в Матвиевская Г. П., 2012, с. 40-44.
- ↑ а б в История математики в Средние века, 1961, с. 156-158.
- ↑ Глейзер Г. И., 1982, с. 81-82.
- ↑ Scott J. F., 1958, с. 50.
- ↑ а б в Сираждинов С. Х., Матвиевская Г. П., 1978, с. 79.
- ↑ а б Scott J. F., 1958, с. 52.
- ↑ а б История математики, том I, 1970, с. 199-201.
- ↑ История математики в Средние века, 1961, с. 157..
- ↑ а б История математики в Средние века, 1961, с. 160.
- ↑ История математики в Средние века, 1961, с. 159.
- ↑ Бахмутская Э. Я. Степенные ряды для sint и cost в работах индийских математиков XV—XVIII вв. // Историко-математические исследования. — М. : Физматгиз, 1960. — Вип. 13.
- ↑ Roy, Ranjan. Discovery of the Series Formula for π by Leibniz, Gregory, and Nilakantha // Mathematics Magazine. — 1990. — Вип. 63 (5). — С. 291–306.
- ↑ Plofker, 2009.
- ↑ История математики, том I, 1970, с. 203.
- ↑ а б Матвиевская Г. П., 2012, с. 51-55.
- ↑ Хрестоматия по истории математики, 1976, с. 204-205.
- ↑ История математики, том I, 1970, с. 236-238..
- ↑ История математики, том I, 1970, с. 234-235.
- ↑ Матвиевская Г. П., 2012, с. 92-96..
- ↑ Матвиевская Г. П., 2012, с. 111.
- ↑ Матвиевская Г. П., 2012, с. 96-98.
- ↑ Матвиевская Г. П., 2012, с. 69.
- ↑ а б Глейзер Г. И., 1983, с. 60.
- ↑ Матвиевская Г. П., 2012, с. 71-78.
- ↑ Хрестоматия по истории математики, 1976, с. 195-198,.
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 82..
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 88..
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А., 1960, с. 105..
- ↑ Цей трактат був поміщений у склад «Астрономії», однієї з шести частин фундаментального теолого-філософсько-наукового трактату «Війни Господа», над яким Гершом працював протягом всього свого життя.
- ↑ Rabinovich, Nachum L. Рабі Леві бен Гершом і походження методу математичної індукції. = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — В. 6. — С. 237—248.
- ↑ Вилейтнер Г., 1960, с. 14, 30-31..
- ↑ Цейтен Г. Г., 1932, с. 223-224..
- ↑ а б в Глейзер Г. И., 1982, с. 79, 84.
- ↑ История математики, том I, 1970, с. 320.
- ↑ Степанов Н. Н. Сферическая тригонометрия. — М.—Л. : ОГИЗ, 1948. — 154 с.
- ↑ Вилейтнер Г., 1960, с. 341-343..
- ↑ Цейтен Г. Г., 1938, с. 126-127.
- ↑ а б Цейтен Г. Г., 1938, с. 129.
- ↑ Александрова Н. В., 2008, с. 189.
- ↑ Рыбников К. А., 1960, с. 125..
- ↑ Цейтен Г. Г., 1938, с. 130-132.
- ↑ а б Глейзер Г. И., 1982, с. 86.
- ↑ Вилейтнер Г., 1960, с. 324-325.
- ↑ Цейтен Г. Г., 1938, с. 283-288.
- ↑ Вилейтнер Г., 1960, с. 327-335.
- ↑ а б История математики, том III, 1972, с. 205-209.
- ↑ Вилейтнер Г., 1960, с. 331.
- ↑ Цейтен Г. Г., 1938, с. 419..
- ↑ O'Connor, J. J.; Robertson, E. F. (February 2005). Biography of Roger Cotes. The MacTutor History of Mathematics. Архів оригіналу за 24 вересня 2012. Процитовано 3 листопада 2012.
- ↑ Александрова Н. В., 2008, с. 152..
- ↑ Александрова Н. В., 2008, с. 80-81..
- ↑ Вилейтнер Г., 1960, с. 322, 329..
- ↑ Александрова Н. В., 2008, с. 207.
- ↑ Вилейтнер Г., 1960, с. 334.
- ↑ История математики, том III, 1972, с. 323.
- ↑ Вилейтнер Г., 1960, с. 148, 336.
- ↑ История математики, том III, 1972, с. 209-215.
- ↑ Тригонометрический ряд // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 5.
- ↑ а б Паплаускас А. Б., 1966, с. 7, 15.
- ↑ Див. статтю Б. А. Розенфельда в книзі: Каган В. Ф. Основания геометрии. Том II, стр. 313—321.
- ↑ Паплаускас А. Б., 1966, с. 26-27..
- ↑ а б в г Тригонометрический ряд // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 5.
- ↑ Паплаускас А. Б., 1966, Глава IV..
- ↑ Даубен, Джозеф У. Георг Кантор и рождение теории трансфинитных множеств // Scientific American, издание на русском языке. — 1983. — Вип. 8 (август). — С. 76–86.
- ↑ Тригонометрический ряд. Архів оригіналу за 23 листопада 2012. Процитовано 28 жовтня 2012.
- ↑ Тригонометрический полином // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия, 1982. — Т. 5.
- ↑ Braunmühl A. Vorlesungen über die Geschichte der Trigonometrie. — Leipzig, 1900—1903.
Література[ред. | ред. код]
- Книги
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб. : ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М. : ГИФМЛ, 1959.
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М. : ГИФМЛ, 1960. — 468 с.
- История математики в школе. VII-VIII классы. Пособие для учителей. — М. : Просвещение, 1982. — 240 с.
- Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М. : Просвещение, 1983. — 352 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. — М. : Наука, 1970. — Т. I.
- История математики. — М. : Наука, 1970. — Т. II.
- История математики. — М. : Наука, 1972. — Т. III.
- Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М. : Либроком, 2012. — 160 с. — ISBN 978-5-397-02777-9.
- Паплаускас А. Б. Тригонометрические рядя. От Эйлера до Лебега. — М. : Наука, 1966. — 277 с.
- Рожанская М. М. Механика на средневековом Востоке. — Москва : Наука, 1976.
- Рыбников К. А. История математики в двух томах. — М. : Изд. МГУ, 1960. — Т. I.
- Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М. : Просвещение, 1978. — 95 с.
- Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. — М. : Просвещение, 1976. — 318 с.
- Цейтен Г. Г. История математики в древности и в средние века. — М.-Л. : ГТТИ, 1932. — 230 с.
- Цейтен Г. Г. История математики в XVI и XVII веках. — М.-Л. : ОНТИ, 1938. — 456 с.
- Юшкевич А. П. История математики в Средние века. — М. : ГИФМЛ, 1961. — 448 с.
- Plofker K. Mathematics in India. — Princeton : Princeton University Press, 2009.
- Scott J. F. A History of Mathematics From Antiquity to the Beginning of the Nineteen Century. — London : Tailor & Francis Ltd, 1958. — 266 p.
- Thurston H. Early astronomy. — New York : Springer-Verlag, 1994.
- Van Brummelen G. The Mathematics of the Heavens and the Earth: The Early History of Trigonometry. — Princeton University Press, 2009.
- Статті
- Веселовский И. Н. Аристарх Самосский — Коперник античного мира // Историко-астрономические исследования, вып. VII. — М., 1961.
- Матвиевская Г. П. Сферика и сферическая тригонометрия в древности и на средневековом Востоке // Развитие методов астрономических исследований, Вып. 8. — М.-Л., 1979.
- Bond J. D. The Development of Trigonometric Methods down to the Close of the XVth Century // Isis. — 1921. — Т. 4, № 2. — С. 295—323.
- Duke D. Hipparchus’ Coordinate System // Arch. Hist. Exact Sci. — 2002. — Т. 56. — С. 427—433.
- Duke D. The Very Early History of Trigonometry // DIO: The International Journal of Scientific History. — 2011. — Т. 17. — С. 34—42.
- Kennedy E. S. The history of trigonometry // Historical Topics for the Mathematics Classroom: Thirty-first Yearbook. — Washington, D.C. : National Council of Teachers of Mathematics, 1969.
- Moussa A. The trigonometric functions, as they were in the arabic-islamic civilization // Arabic Sciences and Philosophy. — 2010. — Т. 20. — С. 93—104.
- Sidoli N. Hipparchus and the Ancient Metrical Methods on the Sphere // Journal of the History of Astronomy. — 2004. — Т. 35. — С. 71—84.
- Toomer G. J. The Chord Table of Hipparchus and the Early History of Greek Trigonometry // Centaurus. — 1973. — Т. 18. — С. 6—28.
- Van der Waerden B. L. Reconstruction of a Greek table of chords // Arch. Hist. Exact Sci. — 1988. — Т. 38. — С. 23—38.
















































