П'ятикутна антипризма

Граф п'ятикутної антипризми
	5-fold symmetry
Вершин	10
Ребер	20
Радіус	3
Діаметр	3
Обхват	3
Хроматичне число	4
Властивості	Регулярний, планарний , Гамільтонів, Ейлерів, квадратичний, циклічний , вершинно-транзитивний

П'ятикутна антипризма

Тип	Призматичний однорідний багатогранник
Властивості	Напівправильний опуклий, рівносторонній, правильногранний, вершинно-транзитивний, конгруентні та коаксікальні основи
Комбінаторика
Елементи	12 граней (10{3}+2{5}); 20 ребер; 10 вершин (4-го степеня).
Грані	10 Правильних трикутників, 2 Правильних п'ятикутників
Характеристика Ейлера	$\chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2$
Конфігурація вершини	3.3.3.5 = 3³.5 В кожній вершині сходяться 3 трикутника та 1 п'ятикутник.
Вершинна фігура	Рівнобедрена трапеція з довжинами сторін 1, 1, 1 та ${\frac {1+{\sqrt {5}}}{2}}$
Класифікація
Позначення	• A₅ (в нотації Конвея^[en] або в нотації Залгаллера) • U_77b (як однорідний багатогранник) • C_34b (в нотації Г. Коксетера)
Символ Шлефлі	$s\left\{{\begin{matrix}2\\5\end{matrix}}\right\}=h\left\{\right\}s\left\{5\right\}$ s{2,10} sr{2,5}
Символ Вітгоффа^[en]	$\| 2 2 5$
Діаграма Коксетера-Динкіна	або (s2s10o) — альтернована^[en] 10-кутна призма^[en]. або (s2s5s) — альтернована діпентагональна призма
Діаграма Шлегеля	A5
Група симетрії	D_5d^[en], [2⁺,10], (2*5), порядок 20 (Діедрична симетрія 5-Антипризми)
Група обертань	D₅, [5,2]⁺, (522), порядок 10
Двоїстий багатогранник	П'ятикутний трапецоедр
Розгортка

П'ятикутна антипри́зма — призматоїд, у якого дві паралельні грані (основи) — рівні між собою правильні п'ятикутники, а решта 10 граней (бокові грані) — правильні трикутники.

Також, п'ятикутна антипри́зма — пряма п'ятикутна рівностороння антипризма.

Має конгруентні та коаксікальні (співвісні) грані основ (правильні п'ятикутники) повернені одна відносно іншої на кут ${\frac {180^{\circ }}{5}}=36^{\circ }$ . Пряма, що сполучає центри основ (вісь антипризми), перпендикулярна до площин основ.

Цей багатогранник є напівправильним багатогранником та однорідним багатогранником.

А отже, володіє такими властивостями:

Всі грані є правильними багатокутниками (двох типів: правильні трикутники та правильні п'ятикутники);
Для будь-якої пари вершин існує симетрія багатогранника (тобто рух, що переводить багатогранник сам в себе), яка переводить одну вершину в іншу.

П'ятикутна антипризма має 6 осей обертової симетрії:

‒ 1 вісь 5-го порядку — проходить через центри п'ятикутних граней; (поворот на 72°, 144°, 216° і 288° або 2π/5, 4π/5, 6π/5, 8π/5 радіан);

‒ 5 осей 2-го порядку — проходять через середини протилежних паралельних ребер основ антипризми (поворот на 180° або $π$ радіан).

П'ятикутна антипризма має 5 площин дзеркальної симетрії, що проходять через вершину та середину протилежного ребра для кожної грані.

Має центр симетрії (в ньому перетинаються всі осі та площини симетрії).

А також є третім багатогранником у нескінченному ряді однорідних антипризм, утворених парним набором трикутних граней та закритих з обох сторін двома багатокутниками.^[1]

Геометрія

Багатогранник є неправильним додекаедром.

П'ятикутну антипризму можна також назвати двічі протилежно відсіченим ікосаедром ‒ тілом, утвореним відсіканням двох п'ятикутних пірамід^[en] з протилежних вершин правильного ікосаедра, залишаючи дві несуміжні п'ятикутні грані.

Пов'язаний багатогранник, двічі косо відсічений ікосаедр^[en] — J₆₂ (один з правильногранних багатогранників Джонсона), аналогічно формується з ікосаедра видаленням двох пірамід; але в цьому багатограннику п'ятикутні грані стикаються ребром.

Дві п'ятикутні грані обох тіл (5-антипризми та J₆₂) можна наростити пірамідами з утворенням ікосаедра.

П'ятикутна антипризма належить до підкласу призматоїдів, та є (виродженим) типом кирпатих багатогранників^[en].

Перерізом п'ятикутної антипризми площиною, що проходить перпендикулярно до осі симетрії п'ятого порядку через її центр, є правильний десятикутник.

Формули

У всіх формулах нижче:

$\varphi =2\cdot \cos \left({\frac {\pi }{5}}\right)={\frac {1+{\sqrt {5}}}{2}}\approx 1.618033988749$ — відношення пропорції «золотого перетину».

(послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).

Діагоналі

Кількість діагоналей опуклого багатогранника: ${\binom {B}{2}}-P$ ,

де В — кількість вершин, Р — кількість ребер багатогранника.

Для п'ятикутної антипризми:

${\binom {10}{2}}-20={\frac {10}{2}}\cdot {\frac {9}{1}}-20=25$ діагоналей (10 граневих та 15 просторових).


Гранева діагональ	$AB={\frac {1+{\sqrt {5}}}{2}}\cdot a=\varphi \cdot a$	≈ 1.6180339887 $\cdot a$
Просторові діагоналі	$AC={\frac {1+{\sqrt {5}}}{2}}\cdot a=\varphi \cdot a$	≈ 1.6180339887 $\cdot a$
Просторові діагоналі	$AD={\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a={\sqrt {\varphi +2}}\cdot a$	≈ 1.9021130326 $\cdot a$

Кут між діагоналями АВ та АС дорівнює 60°.

Метричні характеристики

Для п'ятикутної антипризми з довжиною ребра $a$ :
Радіус описаної сфери (проходить через всі вершини)		$R={\frac {1}{4}}\cdot {\sqrt {4+\csc ^{2}\left({\frac {\pi }{10}}\right)}}\cdot a$	$R={\sqrt {\frac {5+{\sqrt {5}}}{8}}}\cdot a={\frac {\sqrt {\varphi +2}}{2}}\cdot a$	$\approx 0.95105651\cdot a$
Радіус напіввписаної сфери (дотикається до всіх ребер)		$\rho ={\frac {1}{4}}\cdot \csc \left({\frac {\pi }{10}}\right)\cdot a$	$\rho ={\frac {1+{\sqrt {5}}}{4}}\cdot a={\frac {\varphi }{2}}\cdot a$	$\approx 0.80901699\cdot a$
Радіус сфери r₃ та r₅ (дотична до всіх трикутних граней та відповідно, п'ятикутних граней в їх центрах)	Вписаної сфери п'ятикутна антипризма не має		$r_{3}={\frac {\sqrt {42+18{\sqrt {5}}}}{12}}\cdot a$ $={\frac {{\sqrt {3}}\cdot \left(3+{\sqrt {5}}\right)}{12}}\cdot a={\frac {\varphi ^{2}}{2{\sqrt {3}}}}\cdot a$	$\approx 0.7557613\cdot a$
	Вписаної сфери п'ятикутна антипризма не має		$r_{5}={\frac {1}{2}}{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\cdot a$	$\approx 0.4253254\cdot a$
Висота H (Відстань між протилежними п'ятикутними гранями)		$H={\sqrt {1-{\frac {1}{4}}\cdot \sec ^{2}\left({\frac {\pi }{10}}\right)}}\cdot a$	$H={\sqrt {\frac {5+{\sqrt {5}}}{10}}}\cdot a$	$\approx 0.8506508\cdot a$
Площа поверхні		$S={\frac {1}{2}}\cdot 5\left(\mathrm {ctg} \left({\frac {\pi }{5}}\right)+{\sqrt {3}}\right)a^{2}$	$S={\frac {1}{2}}\cdot \left(5{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}$	$\approx 7.7710818\cdot a^{2}$
Об'єм		$V={\frac {5\cdot \sin \left({\frac {3\pi }{10}}\right)\cdot {\sqrt {4\cos ^{2}\left({\frac {\pi }{10}}\right)-1}}}{12\sin ^{2}\left({\frac {\pi }{5}}\right)}}\cdot a^{3}$	$V={\frac {5+2{\sqrt {5}}}{6}}\cdot a^{3}$	$\approx 1.5786893\cdot a^{3}$

Центр мас лежить на осі антипризми і рівновіддалений від її основ.

Кути

Плоскі кути граней при вершині: 60°, 108°

Сума плоских кутів при кожній вершині дорівнює 288°.

Кути багатогранника
Двогранний кут між гранями {3} та {3}	$\alpha =\arccos \left(-{\frac {\sqrt {5}}{3}}\right)=2\cdot \arctan \left(\varphi ^{2}\right)=\pi -2\arctan \left({\frac {3-{\sqrt {5}}}{2}}\right)$	≈ 2.4118649973628 рад ≈ 138° 11′ 22.866375197′′
Двогранний кут між гранями {3} та {5}	$\beta =\arccos \left(-{\sqrt {\frac {5-2{\sqrt {5}}}{15}}}\right)$ $=\pi -\operatorname {arcsec} \left({\sqrt {15+6{\sqrt {5}}}}\right)$	≈ 1.7595068575784 рад ≈ 100° 48′ 44.341068858′′
Тілесний кут при вершині	$\Omega =8\arctan \left({\sqrt {6}}-{\sqrt {5}}\right)+4\arctan \left({\sqrt {3\cdot \left(5+2{\sqrt {5}}\right)}}-{\sqrt {5}}-3\right)$	$\Omega \thickapprox 2.0595584027$ ср
Тілесний кут, під яким п'ятикутну грань видно з центру протилежної п'ятикутної грані	$\Omega _{1}=2\pi -10\cdot \arcsin \left({\sqrt {\frac {15-4{\sqrt {5}}}{29}}}\right)$ $=2\pi -10\cdot \arctan \left({\sqrt {\frac {5-2{\sqrt {5}}}{2}}}\right)$	$\Omega _{1}\thickapprox 1.5373694805$ ср
Сферичність	$\Psi ={\frac {2\cdot {\sqrt[{3}]{5\pi \left(9+4{\sqrt {5}}\right)}}}{5{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}}}}$	$\Psi \thickapprox 0.843724042$

Декартові координати вершин

Декартові координати 10-ти вершин п'ятикутної антипризми з довжиною ребра $a=1$ можна взяти з координат вершин правильного ікосаедра, видаливши з них дві протилежні вершини:

$\left(-{\sqrt {\frac {5+{\sqrt {5}}}{10}}},0,-{\frac {1}{2}}{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),$ $\left({\frac {1}{2}}{\sqrt {\frac {5+2{\sqrt {5}}}{5}}},\pm {\frac {1}{2}},-{\frac {1}{2}}{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),$ $\left(-{\frac {1}{2}}{\sqrt {\frac {5-{\sqrt {5}}}{10}}},\pm {\frac {{\sqrt {5}}+1}{4}},-{\frac {1}{2}}{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right);$
$\left({\sqrt {\frac {5+{\sqrt {5}}}{10}}},0,{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),$ $\left(-{\frac {1}{2}}\cdot {\sqrt {\frac {5+2{\sqrt {5}}}{5}}},\pm {\frac {1}{2}},{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right),$ $\left({\frac {1}{2}}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{10}}},\pm {\frac {{\sqrt {5}}+1}{4}},{\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\right).$

При цьому вершини лежать в двох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного п'ятикутника.

Початок координат збігається з центром багатогранника, що є його центром напіввписаної та описаної сфер.

Вісь Oz збігається з віссю симетрії 5-го порядку.

Площина Oxz є однією з площин симетрії багатогранника.

Граф п'ятикутної антипризми

В теорії графів граф п'ятикутної антипрзми — це граф з 10 вершинами та 20 ребрами, що має кістяк п'ятикутної антипризми.^[2]

Всі 10 вершин графа мають степінь 4, а отже, граф є квадратичним (англ. quartic).

Спектр графа : $Spec(G)=(-{\sqrt {5}})^{2}\left(-1\right)^{4}0^{1}{\sqrt {5}}^{2}4^{1}$

Гамільтонів цикл — замкнений шлях, що проходить через кожну вершину графа рівно один раз.

Деякі гамільтонові цикли графа:

Гамільтонів цикл графа 5-антипризми

{1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 ‒ 9 ‒ 10 — 1}
{1 — 10 — 2 — 9 — 3 — 8 — 4 — 7 ‒ 5 ‒ 6 — 1}
{1 — 10 — 2 — 3 — 9 — 8 — 4 — 7 ‒ 5 ‒ 6 — 1}
{1 — 10 — 2 — 9 — 3 — 4 — 8 — 7 ‒ 5 ‒ 6 — 1}
{1 — 2 — 3 — 9 — 8 — 7 — 4 — 5 ‒ 6 ‒ 10 — 1}

Двоїстий багатогранник

П'ятикутна антипризма має канонічно-двоїстий багатогранник. Середньовписані сфери канонічно двоїстої пари багатогранників збігаються. Для такого способу побудови — двоїстий багатогранник до двоїстого збігається з початковим. Грань двоїстого будується методом Дормана Люка (метод діє лише для однорідних багатогранників).

Канонічно двоїстим багатогранником до 5-антипризми є п'ятикутний трапецоедр.

Має 10 граней: дельтоїди з гострим кутом $\alpha ={\frac {\pi }{5}}rad=36^{\circ }$ та трьома тупими кутами $\beta ={\frac {3\pi }{5}}rad=108^{\circ }$ ;

20 ребер, 12 вершин.

Якщо ребро 5-антипризми дорівнює $a$ , то ребра двоїстого 5-трапецоедра дорівнюють: Коротке ребро: $l={\frac {{\sqrt {5}}-1}{2}}\cdot a=(\varphi -1)\cdot a\approx 0.6180339\cdot a$
Довге ребро: $L={\frac {{\sqrt {5}}+1}{2}}\cdot a=\varphi \cdot a\approx 1.6180339\cdot a$

П'ятикутний трапецоедр
Розгортка п'ятикутного трапецоедра
Поєднання 5-антипризми та 5-трапецоедра

Узагальнення

П'ятикутна антипризма — призматоїд, у якого дві паралельні грані (основи) — рівні між собою 5-кутники, а решта 10 граней (бокові грані) — різносторонні трикутники.

Пряма п'ятикутна антипризма як результат геометричної операції «Альтернування»

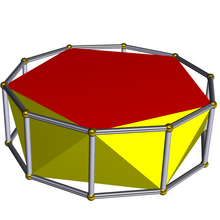
Пряма п'ятикутна антипризма — п'ятикутна антипризма, основами якої є рівні між собою (конгруентні) правильні п'ятикутники, а бокові грані — рівнобедрені трикутники.

Правильна п'ятикутна антипризма — пряма п'ятикутна рівностороння антипризма. В цьому багатограннику бокові грані — правильні трикутники і він, власне, і є однорідною п'ятикутною антипризмою.

Нехай ребра основи мають довжину $a$ , а ребра бічних граней мають довжину $l$ .

Тоді, висота антипризми: $H={\sqrt {l^{2}-{\frac {5-{\sqrt {5}}}{10}}\cdot a^{2}}}$

П'ятикутні грані основ повернені одна відносно іншої навколо осі на кут ${\frac {180^{\circ }}{5}}=36^{\circ }$ (якщо цей кут має інше значення, багатогранник правильніше називати п'ятикутною скрученою призмою).

Пряма, що сполучає центри основ (вісь антипризми), перпендикулярна до площин основ.

Топологічно еквівалентні багатогранники

Скручена п'ятикутна призма^{[pentagonal gyroprism]} (за годинниковою стрілкою або проти годинникової стрілки) може мати те саме розташування вершин, що і пряма п'ятикутна антипризма.

Багатогранник можна отримати з прямої п'ятикутної призми шляхом повороту однієї з її основ навколо осі призми на деякий кут $\varphi \neq {\frac {\pi }{5}}$ . В цьому випадку бокові грані — рівні між собою різносторонні трикутники.

Якщо кут повороту лежить в інтервалі $0<\varphi <{\frac {2\pi }{5}}=72^{\circ }$ , багатогранник буде опуклим. При ${\frac {2\pi }{5}}<\varphi <\pi =180^{\circ }$ , багатогранник буде неопуклим без перетину бокових граней.

Пряма, що сполучає центри основ (вісь антипризми), перпендикулярна до площин основ.^[3].

Схрещена п'ятикутна антипризма — багатогранник, топологічно ідентичний п'ятикутній антипризмі, але його неможливо зробити однорідним ; бічні сторони — рівнобедрені трикутники, а розташування вершин^[en] таке ж, як у п'ятикутної призми.

Багатогранник отримується з прямої призми шляхом повороту однієї з 5-кутної граней навколо осі призми відносно іншої на кут $\varphi ={\frac {6\pi }{5}}=216^{\circ }$ . В цьому випадку бокові грані перетинають одна одну.

Його вершинна конфігурація 3.3/2.3.5 , з одним ретроградним трикутником. Він має d_5d симетрію, порядку 10.

Пов'язані та споріднені багатогранники

П'ятикутна антипризма належить до родини однорідних багатогранників — антипризм і є третім багатогранником в цій родині. До цієї родини також належать тетраедр (вироджена двокутна антипризма), октаедр (трикутна антипризма) та квадратна антипризма.

Родина однорідних n-кутних антипризм
п
о
р
Многогранник												...
Сферична мозаїка												Плоска мозаїка
Конфігурація	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Похідні багатогранники

П'ятикутну антипризму можна наростити п'ятикутною пірамідою, в результаті утвориться багатогранник Джонсона J₁₁ — скручена подовжена п’ятикутна піраміда^[en] .

Якщо п'ятикутну антипризму з довжиною ребра $a$ наростити двома рівносторонніми п'ятикутними пірамідами (що є багатогранниками Джонсона J₂), — утвориться правильний ікосаедр з довжиною ребра $a$ .

При цьому висота нарощених пірамід дорівнює $OH={\sqrt {\frac {5-{\sqrt {5}}}{10}}}\cdot a={\frac {1}{\sqrt {\varphi +2}}}\cdot a\approx 0.525731\cdot a$

Таким чином правильний ікосаедр можна назвати скрученою подовженою п'ятикутною біпірамідою.^[4]

В цьому випадку він має діедричну симетрію 5-Антипризми (D_5d^[en], [2⁺,10], (2*5), порядок 20).

Два однорідних з'єднання багатогранників складаються з п'ятикутних антипризм:


Великий кирпатий додекаедр (з'єднання 6-ти 5-антипризм)	Великий двічі-кирпатий додекаедр (з'єднання 12-ти 5-антипризм)

До п'ятикутної антипризми можуть бути застосовані геометричні операції «зрізання» та «часткове видалення» або «альтернування^[en]» до однієї з форм кирпатих антипризм^[en]:

Кирпаті антипризми
Антипризма A5	Зрізання tA5	Альтернування^[en] sY5 = htA5
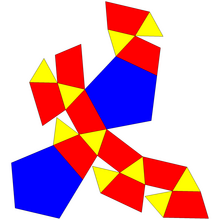
s{2,10}	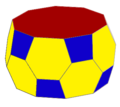ts {2,10}	ss {2,10}
5-антипризма	Зрізана 5-антипризма	Кирпата 5-антипризма
(В:10; Р:20; Г:12)	(В:40; Р:60; Г:22)	(В:20; Р:50; Г:32)

Див. також

Призматичний однорідний многогранник

Примітки

↑ Coxeter, H. S. M. (27 листопада 2012). Regular and Semiregular Polyhedra. Shaping Space. New York, NY: Springer New York. с. 41—52. ISBN 978-0-387-92713-8.
↑ Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs (англ.) . Oxford University Press.
↑ Рисунки скрученных призм и антипризм. Архів оригіналу за 12 грудня 2016. Процитовано 31 січня 2017.
↑ Klitzing, Richard. ike. https://bendwavy.org/klitzing/home.htm (англ.) .

Література

Inorganic Chemistry / A.F. Holleman, Nils Wiberg, Egon Wiberg. — Academic Press, 2001. — ISBN 0-12-352651-5.
W. Peterson, A. Holloway, H. Coyle, M. Williams. Antiprismatic Coordination about Xenon: the Structure of Nitrosonium Octafluoroxenate(VI) // Science. — 1971. — Т. 173, вип. 4003 (16 червня). — ISSN 0036-8075. — Bibcode:1971Sci...173.1238P. — DOI:10.1126/science.173.4003.1238. — PMID 17775218 .
Catherine A. Gorini. The Facts on File Geometry Handbook. — New York : Facts On File, Inc, 2003. — ISBN 0-8160-4875-4.
Norman N. Greenwood, Alan Earnshaw. Chemistry of the Elements (2nd ed.). — Butterworth-Heinemann, 1997. — ISBN 0-08-037941-9.
Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, Хинчин, А. Я. Хинчина. — М. : Государственное издательство физико-математической литературы, 1963. — С. 382-447.

Посилання

Weisstein, Eric W. Antiprism(англ.) на сайті Wolfram MathWorld.
Pentagonal antiprism(англ.) на сайті Polytope Wiki.
Pentagonal Antiprism (англ.) на сайті dmccooey.com.
Klitzing, Richard. "pap".
Quickfur. "The Pentagonal Antiprism"
George W. Hart Prism and Antiprism [Архівовано 28 травня 2017 у Wayback Machine.] (англ.)
PolyhedraMath. A guide to the world of polyhedrons.Prisms and Antiprisms
Pentagonal Antiprism: Interactive Polyhedron Model
Paper Models of Polyhedra [Архівовано 26 лютого 2013 у Wayback Machine.]
- Paper Pentagonal Antiprism
Virtual Reality Polyhedra: The Encyclopedia of Polyhedra

[1] Coxeter, H. S. M. (27 листопада 2012). Regular and Semiregular Polyhedra. Shaping Space. New York, NY: Springer New York. с. 41—52. ISBN 978-0-387-92713-8.

[2] Read, R. C.; Wilson, R. J. (1998). An Atlas of Graphs (англ.) . Oxford University Press.

[3] Рисунки скрученных призм и антипризм. Архів оригіналу за 12 грудня 2016. Процитовано 31 січня 2017.

[bendwavy.org-4] Klitzing, Richard. ike. https://bendwavy.org/klitzing/home.htm (англ.) .

[1]

[2]

[3]

[4]

П'ятикутна антипризма

Зміст

Геометрія