Теорема Тейлора

Вибрані статті із
Числення
Фундаментальна теорема Границя функції Неперервність Теорема Лагранжа Теорема Ролля Теорема про обернену функцію
Диференціальне Визначення Похідна (Таблиця похідних) Диференціал Поняття Нотація Друга похідна Третя похідна Підстановка змінних Неявна функція Теорема Тейлора Правила та тотожності Сума Добуток Частка Степінь Складена функція Обернена функція Формула Фаа ді Бруно
Інтегральне Таблиця інтегралів Визначення Первісна Інтеграл (невласний Рімана Лебега Стілтьєса Даніелла) Інтегрування частинами дисками Методи інтегрування
Рядів Геометричні (Арифметично-геометричні) Гармонічні Знакопереміжні Степеневі Біноміальні Тейлора Ознаки збіжності Ліміт сумування д'Аламбера Радикальна Інтегральна Теорема Лейбніца Діріхле Абеля
Векторів Градієнт Дивергенція Ротор Оператор Лапласа Похідна за напрямком Формули Теореми Градієнтна Гріна Остроградського Стокса
Багатьох змінних Формалізми Матриці Тензорний Зовнішня похідна Визначення Часткова похідна Багатократний інтеграл Криволінійний інтеграл Поверхневий інтеграл Якобіан Матриця Гессе
Спеціалізоване Дробове Стохастичне Варіаційне
інше Історія Математичний аналіз Нестандартний аналіз

Експоненціальна функція y = e^x (суцільна червона лінія) та відповідний многочлен Тейлора четвертого порядку (штрих-пунктирна зелена лінія) поблизу початку координат

Ця стаття про многочлени Тейлора диференційовних функцій. Про ряди Тейлора аналітичних функцій див. відповідну статтю.

Теорема Тейлора дає наближення до функції, що диференціюється k раз, поблизу даної точки за допомогою многочлена Тейлора k-го порядку. Для аналітичних функцій многочлен Тейлора в даній точці є кінцевою послідовністю їх неповного ряду Тейлора, який, у свою чергу, повністю визначає функцію в деякому околі точки. Точний зміст теореми Тейлора до теперішнього часу не узгоджено. Звичайно, існує кілька версій теореми, що застосовуються в різних ситуаціях, і деякі з цих версій містять оцінки помилки, що виникає при наближенні функції за допомогою многочлена Тейлора.

Ця теорема названа на честь математика Брука Тейлора, який сформулював одну з її версій в 1712 році. Явний вираз для помилки наближення було дано набагато пізніше Жозефом Лагранжем. Раніше, в 1671 році, Джеймсом Грегорі вже було згадано наслідок з теореми.

Теорема Тейлора дозволяє опанувати прийомами обчислень початкового рівня, і вона є одним з центральних елементарних інструментів у математичному аналізі. При вивченні математики вона є початковою точкою для вивчення асимптотичного аналізу. Теорема також використовується в математичній фізиці. Вона також узагальнює аналіз функцій декількох змінних і векторні функції f : Rⁿ → R^m для будь-яких вимірів n і m. Це узагальнення теореми Тейлора є базовим для визначення так званих струменів, які з'являються в диференціальній геометрії й в теорії диференціальних рівнянь з частинними похідними.

Передумови для введення теореми

Графік f(x) = e^x (блакитного кольору) з його лінійним наближенням P₁(x) = 1 + x (червоного кольору) в точці a = 0.

Якщо дійснозначна функція f(х) є диференційованою в точці a, то вона має лінійне наближення в точці a. Це означає, що існує функція h₁ така, що

$f(x)=f(a)+f'(a)(x-a)+h_{1}(x)(x-a),\qquad \lim _{x\to a}h_{1}(x)=0.$

Тут

$P_{1}(x)=f(a)+f'(a)(x-a)$

це лінійне наближення функції f в точці a. Графік функції y = P₁(x) є дотичною до графіку функції f в точці x = a. Помилка наближення є такою

$R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(x-a).$

Помітимо, що помилка наближається до нуля трохи скоріше, ніж різниця x − a наближається до нуля відповідно до того як x прагне до a.

Графік f(x)=e^x (блакитного кольору) з квадратичним наближенням P₂(x) = 1 + x + x²/2 (червоного кольору) в точці a = 0. Помітні значні поліпшення наближення.

Якщо ми шукаємо краще наближення f, ми можемо використовувати многочлен другого ступеня замість лінійної функції. Замість знаходження похідної від f в точці a, ми можемо знайти дві похідні, отримавши таким чином многочлен, який так само як і f зростає (або убуває), і так само як і f має опуклість (або увігнутість) в точці a. Многочлен другого ступеня (квадратний многочлен) в цьому випадку буде виглядати наступним чином:

$P_{2}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}.\,$

Теорема Тейлора дозволяє переконатися, що квадратичне наближення, в досить малому околі точки a, є кращим наближенням, ніж лінійне. Зокрема,

$f(x)=P_{2}(x)+h_{2}(x)(x-a)^{2},\qquad \lim _{x\to a}h_{2}(x)=0.$

Тут помилка наближення така

$R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(x-a)^{2}$

що, за умови обмеженості h₂, наближається до нуля швидше, ніж наближається до нуля (x − a)² відповідно до того як x прагне до a.

Наближення функції f(x) = 1/(1 + x²) за допомогою многочленів P_k порядку k = 1, …, 16 відносно точки x = 0 (червоний) та точки x = 1 (салатовий колір). Наближення взагалі не поліпшується за межами (-1,1) і (1-√2,1+√2) відповідно.

Таким чином, якщо використовувати многочлени все вищого ступеня, то будуть отримані все кращі наближення до f. Загалом, помилка в наближенні функції за допомогою поліномів порядку k буде наближатися до нуля трохи швидше, ніж наближається до нуля (x − a)^k відповідно до того як x прагне до a.

Цей наслідок має асимптотичну природу: він лише повідомляє, що помилка R_k наближення за допомогою многочленів Тейлора k-го порядку P_k наближається до нуля швидше, ніж ненульовий многочлен k-го порядку відповідно до того як x → a. Він не повідомляє, наскільки великою є помилка в будь-якому околі центру наближення, але для цього існує формула для залишку (наведена нижче).

Найбільш повні версії теореми Тейлора, як правило, призводять до рівномірних оцінок помилки наближення в малому околі центра наближення, але ці оцінки не є адекватними для околів, які занадто великі, навіть якщо функція f є аналітичною. У цій ситуації слід вибирати кілька многочленів Тейлора з різними центрами наближення, щоб мати надійне Тейлорове наближення до вихідної функції (див. анімований малюнок вище). Можлива також ситуація, коли зростання порядку многочлена не збільшує якість наближення взагалі, навіть якщо функція f диференціюється нескінченну кількість разів. Такий приклад наведено нижче.

Теорема Тейлора для функцій від однієї дійсної змінної

Формулювання теореми

Точне формулювання більшості базових версій теореми наступне.

Теорема Тейлора Нехай k ≥ 1 — ціле, і нехай функція f : R → R — k раз диференційовна в точці a ∈ R. Тоді існує функція h_k : R → R така, що

$f(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+h_{k}(x)(x-a)^{k},\qquad \lim _{x\to a}h_{k}(x)=0.$

Многочлен, що виникає в теоремі Тейлора, є многочленом Тейлора k-го порядку

$P_{k}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}$

функції f в точці a.

Теорема Тейлора описує асимптотичну поведінку залишкового члену

$\ R_{k}(x)=f(x)-P_{k}(x),$

який є помилкою при знаходженні наближення функції f за допомогою многочленів Тейлора. Використовуючи «O» велике та «o» маленьке, теорему Тейлора можна сформулювати так

$R_{k}(x)=o(|x-a|^{k}),\qquad x\to a.$

Формули для залишку

Існує декілька точних формул для залишкового члена R_k многочлена Тейлора, найбільш загальна з яких наступна.

Залишок у формі середнього значення. Нехай функція f : R → R — k+1 раз диференційовна на інтервалі $(a,x)$ та неперервна на відрізку $[a,x]$. Тоді

$\exists \,\xi _{L}\in (a,x):R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}.$

Це залишковий член у формі Лагранжа. За тих же умов

$\exists \,\xi _{C}\in (a,x):R_{k}(x)={\frac {f^{(k+1)}(\xi _{C})}{k!}}(x-\xi _{C})^{k}(x-a).$

Це залишковий член у формі Коші.

Ці уточнення теореми Тейлора зазвичай виводяться за допомогою формули про скінченні прирости.

Можна також знайти й інші вирази для залишку. Наприклад, якщо G(t) є неперервною на закритому інтервалі та диференційовною з похідною, що не прагне до нуля на відкритому інтервалі між a і x, то

$R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G(x)-G(a)}{G'(\xi )}}$

для деякого числа ξ між a і x. Ця версія охоплює форми Лагранжа та Коші як окремі випадки, і виводиться за допомогою теореми Коші про среднє значення (розширеної версії теореми Лагранжа про среднє значення).

Запис формули для залишку в інтегральної формі є більш загальним, ніж попередні формули, і вимагає розуміння інтегральної теорії Лебега. Однак вона зберігається також для інтегралу Рімана за умови, що похідна порядку (k+1) від f є неперервною на закритому інтервалі [a,x].

Інтегральна форма запису формули для залишку Нехай f^(k) — абсолютно неперервна на закритому інтервалі між a і x. Тоді

$R_{k}(x)=\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt.$

Внаслідок абсолютної неперервності f^(k) на закритому інтервалі між a і x, її похідна f^(k+1) існує як L¹-функція, і цей наслідок може бути отриманий за допомогою формальних обчислень з використанням теореми Ньютона — Лейбніца та інтегрування частинами.

Оцінки залишку

На практиці часто буває корисно чисельно оцінити величину залишкового члена наближення Тейлора.

Будемо вважати, що f — (k+1)-раз неперервно диференційовна на інтервалі I, що містить a. Будемо вважати, що існує дійсні постійні числа q і Q такі, що

$q\leqslant f^{(k+1)}(x)\leqslant Q$

на всьому протязі I. Тоді залишковий член задовольняє нерівності

$q{\frac {(x-a)^{k+1}}{(k+1)!}}\leqslant R_{k}(x)\leqslant Q{\frac {(x-a)^{k+1}}{(k+1)!}},$

якщо x > a, і подібна оцінка, якщо x < a. Це простий наслідок з формули залишку в формі Лагранжа. Зокрема, якщо

$|f^{(k+1)}(x)|\leqslant M$

на інтервалі I = (a−r,a+r) з деяким r>0, то

$|R_{k}(x)|\leqslant M{\frac {|x-a|^{k+1}}{(k+1)!}}\leqslant M{\frac {r^{k+1}}{(k+1)!}}$

для всіх x∈(a−r,a+r). Друга нерівність називається рівномірною оцінкою, тому що вона зберігає рівномірність для всіх x на інтервалі (a−r,a+r).

Приклад

Наближення e^x (блакитний) за допомогою многочленів Тейлора P_k порядку k=1,…,7 з центром в точці x=0 (червоний).

Припустимо, ми хочемо знайти наближення функції f(x) = e^x на інтервалі [−1,1] й переконатися, що помилка не перевищує значення 10⁻⁵. У цьому прикладі вважаємо, що нам відомі такі властивості експоненційної функції:

$(*)\qquad e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb {R} .$

З цих властивостей випливає, що f^(k)(x) = e^x для всіх k, і зокрема, f^(k)(0) = 1. Звідси випливає, що многочлен Тейлора k-го порядку функції f в точці 0 та його залишковий член у формі Лагранжа записується за допомогою формули

$P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\qquad R_{k}(x)={\frac {e^{\xi }}{(k+1)!}}x^{k+1},$

де ξ — це деяке число між 0 і x. Оскільки e^x зростає згідно (*), ми можемо використовувати e^x ≤ 1 для x ∈ [−1, 0], щоб оцінити залишок на підінтервалі [−1, 0]. Для знаходження верхньої межі значення залишку на інтервалі [0,1], можемо використовувати властивість e^ξ<<e^x для 0<ξ<x, щоб оцінити

$e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+{\frac {e^{x}}{2}}x^{2},\qquad 0<x\leqslant 1$

використовуючи многочлен Тейлора другого порядку. Висловлюючи з цієї нерівності e^x, приходимо до висновку, що

$e^{x}\leqslant {\frac {1+x}{1-{\frac {x^{2}}{2}}}}=2{\frac {1+x}{2-x^{2}}}\leqslant 4,\qquad 0\leqslant x\leqslant 1$

прийнявши, що чисельник приймає максимальне з усіх своїх можливих значень, а знаменник приймає мінімальне з усіх своїх можливих значень. Використовуючи ці оцінки значень e^x, ми бачимо, що

$|R_{k}(x)|\leqslant {\frac {4|x|^{k+1}}{(k+1)!}}\leqslant {\frac {4}{(k+1)!}},\qquad -1\leqslant x\leqslant 1,$

і необхідна точність досягається в тому випадку, коли

${\frac {4}{(k+1)!}}<10^{-5}\quad \Leftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad \Leftrightarrow \quad k\geq 7.$

(де факторіал 7!=5 040 и 8!=40 320.) Зрештою, теорема Тейлора призводить до наближення

$e^{x}=1+x+{\frac {x^{2}}{2!}}+\ldots +{\frac {x^{7}}{7!}}+R_{7}(x),\qquad |R_{7}(x)|<10^{-5},\qquad -1\leqslant x\leqslant 1.$

Відзначимо, що це наближення дозволяє обчислити значення e≈2.71828 з точністю до п'ятого знака після коми.

Аналітичність

Розкладання Тейлора для дійсних аналітичних функцій

Нехай I⊂R — відкритий інтервал. За означенням, функція f:I→R — дійсна аналітична, якщо вона на даній ділянці визначена збіжністю степеневого ряду. Це означає, що для кожного a ∈ I існує деяке r > 0 і послідовність коефіцієнтів c_k ∈ R така, що (a − r, a + r) ⊂ I і

$f(x)=\sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\cdots ,\qquad |x-a|<r.$

Загалом, радіус збіжності степеневого ряду може бути обчислено за формулою Коші–Адамара

${\frac {1}{R}}=\limsup _{k\to \infty }|c_{k}|^{\frac {1}{k}}.$

Цей результат базується на порівнянні з нескінченно спадною геометричною прогресією, і той же самий метод показує, що якщо степеневий ряд, розкладений по a, збігається для деякого b∈R, він повинен збігатися рівномірно на закритому інтервалі [a − r_b, a + r_b], де r_b = |b − a|. Тут ми тільки розглянули збіжність степеневого ряду, і не виключено, що область (a − R,a + R) розширюється за межі області визначення I функції f.

Многочлен Тейлора від дійсної аналітичної функції f в точці a

$P_{k}(x)=\sum _{j=0}^{k}c_{j}(x-a)^{j},\qquad c_{j}={\frac {f^{(j)}(a)}{j!}}$

це просте усіканням визначеного на деякому інтервалі відповідного степеневого ряду цієї функції, і залишковий член на даному інтервалі подається як аналітична функція

$R_{k}(x)=\sum _{j=k+1}^{\infty }c_{j}(x-a)^{j}=(x-a)^{k}h_{k}(x),\qquad |x-a|<r.$

Тут функція

$h_{k}:(a-r,a+r)\to \mathbb {R} ;\qquad h_{k}(x)=(x-a)\sum _{j=0}^{\infty }c_{k+1+j}(x-a)^{j}$

також є аналітичною, оскільки її степеневий ряд має той же радіус збіжності, що й вихідний ряд. За умови, що [a − r, a + r] ⊂ I і r < R, всі ці ряди збігаються рівномірно на інтервалі (a − r, a + r). Авжеж, у випадку аналітичних функцій можна оцінити залишковий член R_k(x) шляхом «обрізання» послідовності похідних f′(a) у центрі наближення, але при використанні комплексного аналізу з'являються й інші можливості, які описані нижче.

Теорема Тейлора та збіжність ряду Тейлора

Існує розбіжність між многочленами Тейлора диференційовних функцій і рядами Тейлора аналітичних функцій. Можна розглядати (справедливо) ряд Тейлора

$f(x)\approx \sum _{k=0}^{\infty }c_{k}(x-a)^{k}=c_{0}+c_{1}(x-a)+c_{2}(x-a)^{2}+\ldots$

нескінченну кількість разів диференційовної функції f:R→R як її «многочлен Тейлора нескінченно великого порядку» в точці a. Тепер оцінка залишку многочлена Тейлора має на увазі, що для будь-якого порядку k й для будь-якого r>0 існує постійна M_k,r>0 така, що

$(*)\quad |R_{k}(x)|\leqslant M_{k,r}{\frac {|x-a|^{k+1}}{(k+1)!}}$

для кожного x∈(a-r, a+r). Іноді ці постійні можуть бути обрані таким чином, що M_k,r → 0, коли k → ∞ і r залишається незмінною. Тоді ряд Тейлора функції f збігається рівномірно до деякої аналітичної функції

$T_{f}:(a-r,a+r)\to \mathbb {R} ;\qquad T_{f}(x)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.$

Тут необхідно згадати важливий момент. Можлива ситуація, коли нескінченну кількість разів диференційовна функція f має ряд Тейлора в точці a, який збігається в деякому околі точки a, але гранична функція T_f відрізняється від f. Важливим прикладом цього феномену є такий

$f:\mathbb {R} \to \mathbb {R} ;\qquad f(x)={\begin{cases}e^{-{\frac {1}{x^{2}}}}&,x>0,\\0&,x\leqslant 0.\end{cases}}$

Використовуючи ланцюгове правило можна показати індуктивно, що для будь-якого порядку k,

$f^{(k)}(x)={\begin{cases}{\frac {p_{k}(x)}{x^{2k}}}e^{-{\frac {1}{x^{2}}}}&,x>0\\0&,x\leqslant 0\end{cases}}$

для деякого многочлену p_k. Функція $e^{-{\frac {1}{x^{2}}}}$ прагне до нуля швидше, ніж будь-який поліном, відповідно до того, як x → 0, тоді f є нескінченну кількість разів диференційовною й f^(k)(0) = 0 для кожного додатного цілого k. Тепер оцінки для залишку многочлена Тейлора функції f показують, що ряд Тейлора збігається рівномірно до нульової функції на всій дійсній числовій осі. Не буде помилки в наступних твердженнях:

• Ряд Тейлора функції f збігається рівномірно до нульової функції T_f(x)=0.
• Нульова функція є аналітичною, і кожний коефіцієнт її ряду Тейлора дорівнює нулю.
• Функція f є нескінченну кількість разів диференційовною, але не аналітичною.
• Для будь-якого k∈N и r>0 існує M_{k, r}>0 таке, що залишковий член многочлена Тейлора k-го порядку функції f задовільняє умові (*).

Теорема Тейлора в комплексному аналізі

Теорема Тейлора узагальнює функції $f:\mathbb {C} \to \mathbb {C}$, які є комплексно диференційовними на відкритій підмножині U ⊂ C комплексної площини. Однак її корисність знижена іншими теоремами комплексного аналізу, а саме: більш повні версії подібних результатів можуть бути виведені для комплексно диференційовних функцій f : U → C з використанням інтегральної формули Коші як показано нижче.

Нехай r > 0 таке, що замкнене коло B(z, r) ∪ S(z, r) міститься в U. Тоді інтегральна формула Коші з додатною параметризацією γ(t)=re^it околу S(z, r) с t ∈ [0,2π] дає

$f(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}dw,\quad f'(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{2}}}dw,\quad \ldots ,\quad f^{(k)}(z)={\frac {k!}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-z)^{k+1}}}dw.$

Тут всі підінтегральні вирази є неперервними на околі S(z, r), що обґрунтовує диференціювання під знаком інтеграла. Зокрема, якщо f — один раз комплексно диференційовна на відкритій множині U, то вона фактично нескінченну кількість разів комплексно диференційовна на U. Маємо оцінку Коші

$|f^{(k)}(z)|\leqslant {\frac {k!}{2\pi }}\int _{\gamma }{\frac {M_{r}}{|w-z|^{k+1}}}dw={\frac {k!M_{r}}{r^{k}}},\qquad M_{r}=\max _{|w-c|=r}|f(w)|$

для будь-якого z ∈ U и r > 0 таку, що B(z, r) ∪ S(c, r) ⊂ U. Ці оцінки означають, що комплексний ряд Тейлора

$f(z)\approx \sum _{k=0}^{\infty }{\frac {f^{(k)}(c)}{k!}}(z-c)^{k}$

функції f збігається рівномірно в будь-якому колі B(c, r) ⊂ U з S(c, r) ⊂ U в деякій функції T_f. Крім того, використовуючи формулу інтегрування по контуру для похідних f^(k)(c),

${\begin{aligned}T_{f}(z)=\ &\sum _{k=0}^{\infty }{\frac {(z-c)^{k}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{k+1}}}dw={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}\sum _{k=0}^{\infty }{\Big (}{\frac {z-c}{w-c}}{\Big )}^{k}dw\\=\ &{\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-c}}{\Big (}{\frac {1}{1-{\frac {z-c}{w-c}}}}{\Big )}dw={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{w-z}}dw=f(z),\end{aligned}}$

таким чином, будь-яка комплексно диференційовна функція f на відкритій множині U ⊂ C є комплексно аналітичною. Все те, що було написано вище для дійсних аналітичних функцій справедливо також й для комплексних аналітичних функцій, де відкритий інтервал I змінено на відкриту підмножину U ∈ C 1 a — центровані інтервали (a − r, a + r) змінено на c — центровані кола B(c, r). Зокрема, розкладання Тейлора зберігається у вигляді

$f(z)=P_{k}(z)+R_{k}(z),\qquad P_{k}(z)=\sum _{j=0}^{k}{\frac {f^{(k)}(c)}{k!}}(z-c)^{k},$

де залишковий член R_k — комплексно аналітичний. При розгляданні рядів Тейлора методи комплексного аналізу дозволяють отримати кілька більш потужних результатів. Наприклад, використовуючи інтегральну формулу для будь-якої додатно орієнтованої жорданової кривої γ, яка параметризує границю ∂W ⊂ U області W ⊂ U, можна отримати вираз для похідних f^(j)(c) як показано вище, і злегка змінивши розрахунки для T_f(z) = f(z), прийти до точної формули

$R_{k}(z)=\sum _{j=k+1}^{\infty }{\frac {(z-c)^{j}}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(w-c)^{j+1}}}dw={\frac {(z-c)^{k+1}}{2\pi i}}\int _{\gamma }{\frac {f(w)dw}{(w-c)^{k+1}(w-z)}},\qquad z\in W.$

Важлива особливість тут в тому, що якість наближення за допомогою многочлена Тейлора в області W ⊂ U є мажоріруємим значенням функції f на границі ∂W ⊂ U. Також, застосовуючи оцінки Коші до виразу залишку ряду, отримуємо рівномірні оцінки

$|R_{k}(z)|\leqslant \sum _{j=k+1}^{\infty }{\frac {M_{r}|z-c|^{j}}{r^{j}}}={\frac {M_{r}}{r^{k+1}}}{\frac {|z-c|^{k+1}}{1-{\frac {|z-c|}{r}}}}\leqslant {\frac {M_{r}\beta ^{k+1}}{1-\beta }},\qquad {\frac {|z-c|}{r}}\leqslant \beta <1.$

Приклад

Графік комплексної функції f(z) = 1/(1 + z²). Модуль показано висотою підйому та аргумент показано кольором: ціан=0, синій=π/3, фіолетовий=2π/3, червоний=π, жовтий=4π/3, зелений=5π/3.

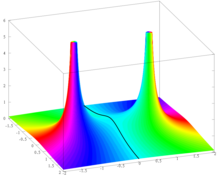
Функція f:R→R, що визначається рівнянням

$f(x)={\frac {1}{1+x^{2}}}$

дійсна аналітична, тобто в даній області визначається своїм рядом Тейлора. Один з малюнків, наведених вище [Архівовано 19 вересня 2015 у Wayback Machine.], показує, що деякі функції, що задаються дуже просто, не можуть бути виражені за допомогою наближення Тейлора в околі центру наближення, якщо цей окіл занадто великий. Цю властивість легко зрозуміти в рамках комплексного аналізу. Більш конкретно, функція f розширюється до мероморфної функції

$f:\mathbb {C} \cup \{\infty \}\to \mathbb {C} \cup \{\infty \};\quad f(z)={\frac {1}{1+z^{2}}}$

на компактифіцированій комплексній площині. Вона має прості осі в точках z=i и z=−i, і вона всюди аналітична. ЇЇ ряд Тейлора, що має центр в z₀, збігається на будь-якому колі B(z₀,r) с r<|z-z₀|, де той же ряд Тейлора збігається при z∈C. Внаслідок цього ряд Тейлора функції f, що має центр в точці 0, збігається на B(0,1) і він не збігається для будь-якого z∈C с |z|>1 внаслідок наявних осей в точках i и −i. За тих же причин ряд Тейлора функції f, що має центр в точці 1, збігається на B(1,√2) і не збігається для будь-якого z∈C с |z-1|>√2.

Узагальнення теореми Тейлора

Вищі порядки диференційовності

Функція f:Rⁿ → R — диференційовна в точці a ∈ Rⁿ тоді й тільки тоді, коли існує лінійна форма L : Rⁿ → R і функція h : Rⁿ → R така, що

$f({\boldsymbol {x}})=f({\boldsymbol {a}})+L({\boldsymbol {x}}-{\boldsymbol {a}})+h({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}}),\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h({\boldsymbol {x}})=0.$

Якщо цей випадок має місце, то L = df(a) є диференціал функції f в точці a. Крім того, коли частинні похідні функції f існують в точці a, то диференціал f в точці a визначено формулою

$df({\boldsymbol {a}})({\boldsymbol {v}})={\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_{1}+\cdots +{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})v_{n}.$

Вводячи мультиіндекс, запишемо

$|\alpha |=\alpha _{1}+\cdots +\alpha _{n},\quad \alpha !=\alpha _{1}!\cdots \alpha _{n}!,\quad {\boldsymbol {x}}^{\alpha }=x_{1}^{\alpha _{1}}\cdots x_{n}^{\alpha _{n}}$

для α ∈ Nⁿ і x ∈ Rⁿ. Якщо всі частинні похідні k-го порядку функції f : Rⁿ → R — неперервні в a ∈ Rⁿ, то згідно з теоремою Клеро, можна змінити порядок змішаних похідних в точці a, тоді запис

$D^{\alpha }f={\frac {\partial ^{|\alpha |}f}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{n}^{\alpha _{n}}}},\qquad |\alpha |\leqslant k$

для частинних похідних вищих порядків є правомірним у цій ситуації. Теж саме є правильним, якщо всі частинні похідні (k − 1)-го порядку функції f існують в деякому околі точки a і диференційовні в точці a. Тоді можна сказати, що функція f — k разів диференційовна в точці a .

Теорема Тейлора для функцій багатьох змінних

Теорема Тейлора для функцій багатьох змінних. Нехай f : Rⁿ → R — k разів диференційовна функція в точці a∈Rⁿ. Тоді існує h_α : Rⁿ→R така, що

$f({\boldsymbol {x}})=\sum _{|\alpha |=0}^{k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\alpha |=k}h_{\alpha }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha },\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h_{\alpha }({\boldsymbol {x}})=0.$

Якщо функція f : Rⁿ → R — k+1 разів неперервно диференційовна в замкненій кулі B, то можна отримати точну формулу для залишку розкладання Тейлора до частинних похідних (k+1)-го порядку від f в цьому околі. А саме

$f({\boldsymbol {x}})=\sum _{|\alpha |=0}^{k}{\frac {D^{\alpha }f({\boldsymbol {a}})}{\alpha !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\beta |=k+1}R_{\beta }({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\beta },\qquad R_{\beta }({\boldsymbol {x}})={\frac {|\beta |}{\beta !}}\int _{0}^{1}(1-t)^{|\beta |-1}D^{\beta }f{\big (}{\boldsymbol {a}}+t({\boldsymbol {x}}-{\boldsymbol {a}}){\big )}\,dt.$

У цьому випадку, внаслідок неперервності частинних похідних (k+1)-го порядку на компактній множині B, безпосередньо отримуємо

${\big |}R_{\beta }({\boldsymbol {x}})|\leqslant {\frac {|\beta |}{\beta !}}\max _{|\alpha |=|\beta |}\max _{{\boldsymbol {y}}\in B}|D^{\alpha }f({\boldsymbol {y}})|,\qquad {\boldsymbol {x}}\in B.$

Докази

Доказ теореми Тейлора для однієї дійсної змінної

Нехай

$h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(x-a)^{k}}}&x\not =a\\0&x=a\end{cases}}$

де, як вказано в формулюванні теореми Тейлора,

$P(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.$

Достатньо показати, що

$\lim _{x\to a}h_{k}(x)=0.\,$

Доказ засновано на повторюваному застосуванні правила Лопіталя. Помітимо, що кожне j = 0,1,…,k−1, $f^{(j)}(a)=P^{(j)}(a)$. Звідси кожна наступна похідна чисельника функції $h_{k}(x)$ прагне до нуля в точці $x=a$, і теж саме справедливо для знаменника. Тоді

${\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))}{{\frac {d^{k-1}}{dx^{k-1}}}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{x-a}}\\&={\frac {1}{k!}}(f^{(k)}(a)-P^{(k)}(a))=0\end{aligned}}$

де перехід від передостаннього виразу до останнього випливає з визначення похідної в точці x = a.

Джерела

• Apostol, Tom (1967), Calculus, Jon Wiley & Sons, Inc., ISBN 0-471-00005-1.
• Bartle; Sherbert (2000), Introduction to Real Analysis (вид. 3rd), John Wiley & Sons, Inc., ISBN 0-471-32148-6.
• Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer-Verlag, ISBN 978-3540006626.
• Klein, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6.
• Pedrick, George (1994), A First Course in Analysis, Springer-Verlag, ISBN 0-387-94108-8.
• Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, Inc., ISBN 978-0534980122.
• Rudin, Walter (1987), Real and complex analysis, 3rd ed., McGraw-Hill Book Company, ISBN 0-07-054234-1.

Посилання

• Формула Тейлора // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 277. — 594 с.
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2023. — 1900+ с.(укр.)
• Taylor Series Approximation to Cosine [Архівовано 4 січня 2010 у Wayback Machine.]
• Trigonometric Taylor Expansion [Архівовано 10 листопада 2007 у Wayback Machine.] interactive demonstrative applet
• Taylor Series Revisited [Архівовано 5 червня 2009 у Wayback Machine.] at Holistic Numerical Methods Institute [Архівовано 6 вересня 2006 у Wayback Machine.]