Кореляція

У статистиці кореля́ція (англ. correlation) або зале́жність (англ. dependence) — це будь-який статистичний взаємозв'язок, причинний чи ні, між двома випадковими змінними або двовимірними даними[en]. Хоч у найширшому сенсі «кореляція» й може вказувати на будь-який тип пов'язаності, у статистиці вона зазвичай означає ступінь, до якого пара змінних пов'язані лінійно. До добре відомих прикладів залежних явищ належать кореляція між зростом батьків та їхніх нащадків, а також кореляція між ціною товару та кількістю, яку споживачі готові придбати, як це зображують на так званій кривій попиту.
Кореляції корисні, бо вони можуть вказувати на передбачальний зв'язок, який можливо використовувати на практиці. Наприклад, енергогенерувальна компанія може виробляти менше електроенергії в день з помірною погодою на основі кореляції між попитом на електроенергію та погодою. У цьому прикладі існує причинно-наслідковий зв'язок, оскільки екстремальна погода змушує людей використовувати більше електроенергії для опалення чи кондиціювання. Проте в загальному випадку, щоби зробити висновок про наявність причинно-наслідкового зв'язку, наявності кореляції недостатньо (тобто, кореляція не означає спричинювання).
Формально випадкові змінні залежні, якщо вони не задовольняють математичній властивості ймовірнісної незалежності. Неформальною мовою кореляція є синонімом залежності. Проте при використанні в технічному сенсі кореляція означає будь-яку з декількох конкретних типів математичних операцій між випробуваними змінними та їхніми відповідними математичними сподіваннями. По суті, кореляція — це міра того, як дві чи більше змінні пов'язані одна з одною. Існує декілька коефіцієнтів кореляції, часто позначуваних через або , які вимірюють ступінь кореляції. Найпоширеніший з них — коефіцієнт кореляції Пірсона, чутливий лише до лінійного взаємозв'язку між двома змінними (який може мати місце, навіть якщо одна змінна є нелінійною функцією іншої). Інші коефіцієнти кореляції — наприклад, рангову кореляцію Спірмена, — було розроблено для більшої робастності, ніж в пірсонового, тобто більшої чутливості до нелінійних взаємозв'язків.[1][2][3] Для вимірювання взаємозалежності двох змінних також можливо застосовувати взаємну інформацію.

Найбільш загальновідомою мірою залежності між двома величинами є коефіцієнт кореляції моменту добутку Пірсона (англ. Pearson product-moment correlation coefficient, PPMCC), або «коефіцієнт кореляції Пірсона» (англ. Pearson's correlation coefficient), який зазвичай називають просто «коефіцієнт кореляції» (англ. the correlation coefficient). Його отримують взяттям відношення коваріації двох розгляданих змінних нашого чисельного набору даних, унормованої квадратним коренем їхніх дисперсій. Математично, коваріацію цих двох змінних просто ділять на добуток їхніх стандартних відхилень. Карл Пірсон розробив цей коефіцієнт на основі подібної, але дещо відмінної ідеї Френсіса Гальтона.[4]
Коефіцієнт кореляції Пірсона намагається встановити лінію, яка найкраще допасовується до набору даних із двох змінних, по суті викладаючи очікувані значення, а отриманий коефіцієнт кореляції Пірсона вказує, наскільки далеким від очікуваних значень є фактичний набір даних. Залежно від знаку нашого коефіцієнта кореляції Пірсона ми можемо отримати як від'ємну, так і додатну кореляцію, якщо якийсь зв'язок між змінними нашого набору даних існує.[джерело?]
Генеральний коефіцієнт кореляції (англ. population correlation coefficient) між двома випадковими змінними та з математичними сподіваннями та та стандартними відхиленнями та визначають як
де — оператор математичного сподівання, означає коваріацію, а — широко вживане альтернативне позначення коефіцієнту кореляції. Кореляція Пірсона визначається лише в тому випадку, якщо обидва стандартні відхилення є скінченними й додатними. Альтернативною формулою чисто в термінах моментів є
Наслідком нерівності Коші — Буняковського є те, що модуль коефіцієнта кореляції Пірсона не перевищує 1. Таким чином, значення коефіцієнта кореляції лежать у проміжку з −1 по +1. Коефіцієнт кореляції дорівнює +1 у випадку ідеального прямого (висхідного) лінійного взаємозв'язку (кореляції), −1 у випадку ідеального зворотного (спадного) лінійного взаємозв'язку (антикореля́ція, англ. anti-correlation),[5] і деякому значенню в інтервалі у всіх інших випадках, показуючи ступінь лінійної залежності між змінними. У міру його наближення до нуля взаємозв'язок послаблюється (ближче до некорельованих). Що ближчий цей коефіцієнт до −1 чи 1, то сильніша кореляція між змінними.
Якщо змінні незалежні, то коефіцієнт кореляції Пірсона дорівнює 0, але зворотне не істинне, оскільки коефіцієнт кореляції виявляє лише лінійні залежності між двома змінними. Простіше кажучи, якщо дві випадкові змінні та незалежні, то вони некорельовані, але якщо дві випадкові змінні некорельовані, то вони можуть бути, а можуть і не бути незалежними.
Наприклад, припустімо, що випадкова змінна симетрично розподілена навколо нуля, а . Тоді цілком визначено через , тож та цілком залежні, але їхня кореляція дорівнює нулеві: вони некорельовані. Проте в особливому випадку, коли та спільно нормальні[en], некорельованість рівнозначна незалежності.
Незважаючи на те, що некорельованість даних не обов'язково означає незалежність, можливо пересвідчуватися, що випадкові змінні незалежні, якщо їхня взаємна інформація дорівнює 0.
За заданого ряду з вимірів пари , пронумерованих за , для оцінювання генеральної кореляції Пірсона між та можливо використовувати ви́бірковий коефіцієнт кореляції (англ. sample correlation coefficient). Цей вибірковий коефіцієнт кореляції визначають як
де та — вибіркові середні значення та , а та — скориговані вибіркові стандартні відхилення та .
Еквівалентними виразами для є
де та — нескориговані вибіркові стандартні відхилення та .
Якщо та — результати вимірювань, що містять похибку вимірювання, то реалістичні межі коефіцієнта кореляції становлять не від −1 до +1, а менший проміжок.[6] Для випадку лінійної моделі з єдиною незалежною змінною коефіцієнтом детермінації (R-квадрат) є квадрат , коефіцієнту кореляції Пірсона.
Розгляньмо спільний розподіл імовірності X та Y, наведений у таблиці нижче.
- yx
−1 0 1 0 0 1/3 0 1 1/3 0 1/3
Відособлені розподіли для цього спільного розподілу:
Це дає наступні математичні сподівання та дисперсії:
Отже,
Коефіцієнти рангової кореляції, як-от коефіцієнт рангової кореляції Спірмена та коефіцієнт рангової кореляції Кендалла (τ), вимірюють, до якої міри в разі збільшення однієї змінної інша змінна схильна збільшуватися, не вимагаючи, щоби це збільшення було подано лінійною залежністю. Якщо за збільшення однієї змінної інша зменшується, то коефіцієнти рангової кореляції будуть від'ємними. Ці коефіцієнти рангової кореляції часто розглядають як альтернативи коефіцієнту Пірсона, яку використовують або для зменшення кількості обчислень, або для того, щоби зробити коефіцієнт менш чутливим до не нормальності в розподілах. Проте ця точка зору має мало математичних підстав, оскільки коефіцієнти рангової кореляції вимірюють інший тип зв'язку, ніж коефіцієнт кореляції Пірсона, і їх найкраще розглядати як показники іншого типу зв'язку, а не як альтернативну міру генерального коефіцієнту кореляції.[7][8]
Щоби унаочнити природу рангової кореляції та її відмінність від лінійної кореляції, розгляньмо наступні чотири пари чисел :
- (0, 1), (10, 100), (101, 500), (102, 2000).
В міру просування від кожної пари до наступної збільшується, й те саме робить . Цей взаємозв'язок ідеальний, у тому сенсі, що збільшення в завжди супроводжується збільшенням в . Це означає, що ми маємо ідеальну рангову кореляцію, й обидва коефіцієнти кореляції Спірмена та Кендалла дорівнюють 1, тоді як у цьому прикладі коефіцієнт кореляції Пірсона дорівнює 0,7544, вказуючи на те, що точки далеко не лежать на одній прямій. Так само, якщо завжди зменшується, коли збільшується, коефіцієнти рангової кореляції становитимуть −1, тоді як коефіцієнт кореляції Пірсона може бути або не бути близьким до −1, залежно від того, наскільки близько до прямої лінії розташовані ці точки. Хоча в граничних випадках ідеальної рангової кореляції ці два коефіцієнти рівні (чи то обидва +1, чи обидва −1), зазвичай це не так, і тому значення цих двох коефіцієнтів неможливо порівнювати змістовно.[7] Наприклад, для трьох пар (1, 1) (2, 3) (3, 2) коефіцієнт Спірмена дорівнює 1/2, а коефіцієнт Кендалла дорівнює 1/3.
Інформації, яку надає коефіцієнт кореляції, недостатньо для визначення структури залежності між випадковими змінними.[9] Коефіцієнт кореляції повністю визначає структуру залежності лише в дуже окремих випадках, наприклад, коли розподіл є багатовимірним нормальним розподілом (див. рисунок вище). У випадку еліптичних розподілів він характеризує (гіпер-)еліпси рівної густини, проте він не повністю характеризує структуру залежності (наприклад, ступені вільності багатовимірного t-розподілу[en] визначають рівень хвостової залежності).
Для подолання того недоліку кореляції Пірсона, що вона може бути нульовою для залежних змінних, було запропоновано кореляцію по віддалі[en] (англ. distance correlation),[10][11] нульова кореляція по віддалі означає незалежність.
Рандомізований коефіцієнт залежності (РКЗ, англ. Randomized Dependence Coefficient, RDC)[12] — це обчислювально ефективна міра залежності між багатовимірними випадковими змінними на основі копул. РКЗ інваріантний щодо нелінійного масштабування випадкових змінних, здатний виявляти широкий спектр моделей функціональних асоціацій, і набуває нульового значення при незалежності.
Для двох бінарних змінних[en] відношення шансів[en] вимірює їхню залежність і набуває діапазону невід'ємних чисел, потенційно нескінченних:. Схожі статистики, як-от Y Юла[en] та Q Юла[en], унормовують його до подібного на кореляцію проміжку . Відношення шансів узагальнено логістичною моделлю для моделювання випадків, коли залежні змінні є дискретними, й може бути одна або декілька незалежних змінних.
Кореляційне відношення[en], взаємна інформація на основі ентропії, повна кореляція[en], двоїста повна кореляція[en] та поліхорна кореляція[en] також здатні виявляти загальніші залежності, як і розгляд копули між ними, тоді як коефіцієнт детермінації узагальнює коефіцієнт кореляції до множинної регресії[en].
Ступінь залежності між змінними X та Y не залежить від масштабу, в якому виражено ці змінні. Тобто, якщо ми аналізуємо взаємозв'язок між X та Y, перетворення X на a + bX й Y на c + dY, де a, b, c та d є сталими (b та d додатні), на більшість мір кореляції не впливає. Це стосується деяких кореляційних статистик, а також їхніх генеральних аналогів. Деякі кореляційні статистики, як-от коефіцієнт рангової кореляції, також інваріантні щодо монотонних перетворень відособлених розподілів X та/або Y.
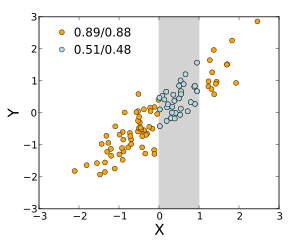
Більшість мір кореляції чутливі до способу вибирання X та Y. Залежності, як правило, сильніші, якщо розглядати їх на ширшому діапазоні значень. Таким чином, якщо ми розглянемо коефіцієнт кореляції між зростом батьків та їхніх синів над усіма дорослими чоловіками, та порівняємо його з тим же коефіцієнтом кореляції, розрахованим, коли вибрано батьків зростом від 165 см до 170 см, то в останньому випадку кореляція буде слабшою. Було розроблено кілька методик, які намагаються виправляти обмеження діапазону в одній або обох змінних, і які зазвичай використовують в метааналізі; найпоширенішими є рівняння Торндайка другого та третього випадків.[13]
Деякі використовувані міри кореляції можуть бути невизначеними для певних спільних розподілів X та Y. Наприклад, коефіцієнт кореляції Пірсона визначено в термінах моментів, і, отже, буде не визначено, якщо не визначено моменти. Завжди визначено міри залежності, які ґрунтуються на квантилях. Статистики на основі вибірки, призначені оцінювати генеральні міри залежності, можуть мати або не мати бажаних статистичних властивостей, наприклад бути незміщеними та асимптотично слушними, залежно від просторової структури сукупності, з якої було вибрано дані.
Чутливість до розподілу даних можливо використовувати як перевагу. Наприклад, масштабну кореляцію[en] розроблено так, щоби використовувати чутливість до діапазону задля вихоплювання кореляції між швидкими складовими часових рядів.[14] Шляхом контрольованого зменшення діапазону значення кореляції на довгому часовому масштабі відфільтровуються, й виявляються лише кореляції на коротких часових масштабах.
Кореляційна матриця випадкових змінних — це матриця , чиїм елементом є
Таким чином, всі її діагональні елементи однаково одиничні. Якщо всі використовувані міри кореляції є коефіцієнтами кореляції Пірсона, то кореляційна матриця така же, як і коваріаційна матриця стандартизованих випадкових змінних для . Це стосується як генеральної кореляційної матриці (у цьому випадку — генеральне стандартне відхилення), так і ви́біркової кореляційної матриці (у цьому випадку позначує вибіркове стандартне відхилення). Отже, кожна з них обов'язково є додатно напіввизначеною матрицею. Більше того, кореляційна матриця строго додатно визначена, якщо жодна змінна не може мати всі свої значення точно породженими як лінійна функція значень інших.
Кореляційна матриця симетрична, оскільки кореляція між та це те саме, що й кореляція між та .
Кореляційна матриця з'являється, наприклад, в одній формулі для коефіцієнта множинної детермінації[en], міри допасованості у множинній регресії[en].
У статистичному моделюванні кореляційні матриці, що подають зв'язки між змінними, категоризують до різних кореляційних структур, які розрізнюють за такими чинниками як кількість параметрів, необхідних для їхнього оцінювання. Наприклад, у взаємозамінній[en] кореляційній матриці всі пари змінних змодельовано як такі, що мають однакову кореляцію, так що все недіагональні елементи матриці дорівнюють один одному. З іншого боку, авторегресійну матрицю часто використовують, коли змінні подають часовий ряд, оскільки кореляції, ймовірно, будуть більшими, коли вимірювання ближчі в часі. До інших прикладів належать незалежні, неструктуровані, M-залежні матриці, та матриці Тепліца.
В розвідувальному аналізі даних іконографія кореляцій[en] полягає в заміні кореляційної матриці діаграмою, де «визначні» кореляції подають суцільною лінією (додатна кореляція), або пунктирною лінією (від'ємна кореляція).
У деяких застосуваннях (наприклад, побудові моделей даних з лише частково спостережуваних даних) потрібно знаходити «найближчу» кореляційну матрицю до «приблизної» кореляційної матриці (наприклад, матриці, якій зазвичай бракує напіввизначеної додатності через те, яким чином її було обчислено).
2002 року Хаєм[15] формалізував поняття близькості за допомогою норми Фробеніуса та запропонував метод обчислення найближчої кореляційної матриці за допомогою проєкційного алгоритму Дикстри[en], втілення якого доступне як інтерактивний вебППІ[en].[16]
Це викликало інтерес до даного предмета, з отриманими в наступні роки новими теоретичними (наприклад, обчислення найближчої кореляційної матриці з факторною структурою[17]) та чисельними (наприклад, використання методу Ньютона для обчислення найближчої кореляційної матриці[18]) результатами.
Аналогічно для двох стохастичних процесів та : Якщо вони незалежні, то вони некорельовані.[19] Протилежне цьому твердженню може бути неправильним. Навіть якщо дві змінні не корельовані, вони можуть не бути незалежними одна від одної.
Поширений вислів «корелювання не означає спричинювання» означає, що кореляцію неможливо використовувати саму по собі для висновування причинно-наслідкового зв'язку між змінними.[20] Цей вислів не слід сприймати так, що кореляції не можуть вказувати на потенційне існування причинно-наслідкових зв'язків. Проте причини, що лежать в основі кореляції, якщо вони й існують, можуть бути непрямими або невідомими, а високі кореляції також перекриваються з відношеннями тотожності (тавтології), де процесу спричинювання не існує. Отже, кореляція між двома змінними не є достатньою умовою для встановлення причинно-наслідкового зв'язку (в будь-якому з напрямків).
Кореляція між віком та зростом у дітей є досить причиннісно прозорою, але кореляція між настроєм і здоров'ям у людей — не настільки. Чи поліпшення настрою призводить до покращення здоров'я, чи гарне здоров'я призводить до гарного настрою, чи обидва? Чи якийсь інший чинник лежить в основі обох? Іншими словами, кореляцію можна вважати свідченням можливого причинно-наслідкового зв'язку, але вона не може вказувати, яким може бути причинний зв'язок, якщо він взагалі існує.

Коефіцієнт кореляції Пірсона показує силу лінійного взаємозв'язку між двома змінними, але його значення, як правило, характеризує їхній взаємозв'язок не повністю.[21] Зокрема, якщо умовне середнє за заданого , позначуване через , не лінійне за , то коефіцієнт кореляції не повністю визначатиме вигляд .
На сусідньому зображенні показано діаграми розсіювання квартету Анскомбе, набору з чотирьох різних пар змінних, створеного Френсісом Анскомбе[en].[22] Чотири змінні мають однакове середнє значення (7,5), дисперсію (4,12), кореляцію (0,816) та лінію регресії (). Проте, як видно на цих графіках, розподіл змінних дуже різний. Перші (вгорі ліворуч) видаються розподіленими нормально й відповідають тому, що можна було би очікувати, розглядаючи дві змінні, які корелюють, й дотримуються припущення нормальності. Другі (вгорі праворуч) розподілено не нормально, і хоча й можливо спостерігати очевидний взаємозв'язок між цими двома змінними, він не є лінійним. У цьому випадку коефіцієнт кореляції Пірсона не вказує, що існує точна функційна залежність: лише ступінь, до якого цей взаємозв'язок можливо наблизити лінійним співвідношенням. У третьому випадку (внизу ліворуч) лінійна залежність є ідеальною, за винятком одного викиду, який чинить достатній вплив, щоби знизити коефіцієнт кореляції з 1 до 0,816. Нарешті, четвертий приклад (унизу праворуч) показує інший приклад, коли одного викиду достатньо для отримання високого коефіцієнта кореляції, навіть якщо взаємозв'язок між двома змінними не є лінійним.
Ці приклади показують, що коефіцієнт кореляції як зведена статистика не здатен замінити візуальне дослідження даних. Іноді кажуть, що ці приклади демонструють, що кореляція Пірсона передбачає, що дані мають нормальний розподіл, але це правильно лише частково.[4] Кореляцію Пірсона можливо точно розрахувати для будь-якого розподілу, який має скінченну коваріаційну матрицю, що включає більшість розподілів, які зустрічаються на практиці. Проте, достатньою статистикою коефіцієнт кореляції Пірсона (взятий разом із вибірковим середнім значенням та дисперсією) є лише в тому випадку, якщо дані взято з багатовимірного нормального розподілу. В результаті, коефіцієнт кореляції Пірсона повністю характеризує зв'язок між змінними тоді й лише тоді, коли дані вибирають із багатовимірного нормального розподілу.
Якщо пара випадкових змінних слідує двовимірному нормальному розподілу, то умовне середнє є лінійною функцією від , а умовне середнє є лінійною функцією від Коефіцієнт кореляції між та й відособлені середні значення та дисперсії та визначають цю лінійну залежність:
де та — математичні сподівання та відповідно, а та — стандартні відхилення та відповідно.
Емпірична кореляція — це оцінка коефіцієнта кореляції Оцінку розподілу для задають через
де — гауссова гіпергеометрична функція.
Ця густина є одночасно баєсовою апостеріорною густиною, й точною оптимальною густиною довірчого розподілу[en].[23][24]
- Автокореляція
- Взаємна кореляція
- Відношення квадрантових кількостей[en]
- Внутрішньокласова кореляція[en]
- Генетична кореляція[en]
- Залежність середнього значення[en]
- Екологічна кореляція[en]
- Іконографія кореляцій[en]
- Ілюзорна кореляція
- Канонічна кореляція
- Коваріація
- Коваріація та кореляція
- Коефіцієнт детермінації
- Коефіцієнт конкордації[en]
- Коінтеграція[en]
- Кореляційна функція
- Кореляційний розрив[en]
- Кофенетична кореляція[en]
- Лямбда Гудмана і Крускала[en]
- Міжкласова кореляція[en]
- Множинна кореляція[en]
- Непояснена частка дисперсії[en]
- Підіймання (добування даних)[en]
- Проблема змінності ареальних одиниць[en]
- Помилкова кореляція
- Слабка незалежність[en]
- Статистичне кореляційне відношення[en]
- Точково-бісеріальний коефіцієнт кореляції[en]
- ↑ Croxton, Frederick Emory; Cowden, Dudley Johnstone; Klein, Sidney (1968) Applied General Statistics (англ.), Pitman. ISBN 9780273403159 (page 625)
- ↑ Dietrich, Cornelius Frank (1991) Uncertainty, Calibration and Probability: The Statistics of Scientific and Industrial Measurement 2nd Edition (англ.), A. Higler. ISBN 9780750300605 (Page 331)
- ↑ Aitken, Alexander Craig (1957) Statistical Mathematics 8th Edition (англ.). Oliver & Boyd. ISBN 9780050013007 (Page 95)
- ↑ а б Rodgers, J. L.; Nicewander, W. A. (1988). Thirteen ways to look at the correlation coefficient. The American Statistician (англ.). 42 (1): 59—66. doi:10.1080/00031305.1988.10475524. JSTOR 2685263.
- ↑ Dowdy, S. and Wearden, S. (1983). "Statistics for Research" (англ.), Wiley. ISBN 0-471-08602-9 pp 230
- ↑ Francis, DP; Coats AJ; Gibson D (1999). How high can a correlation coefficient be?. Int J Cardiol (англ.). 69 (2): 185—199. doi:10.1016/S0167-5273(99)00028-5. PMID 10549842.
- ↑ а б Yule, G.U and Kendall, M.G. (1950), "An Introduction to the Theory of Statistics", 14th Edition (5th Impression 1968) (англ.). Charles Griffin & Co. pp 258–270
- ↑ Kendall, M. G. (1955) "Rank Correlation Methods" (англ.), Charles Griffin & Co.
- ↑ Mahdavi Damghani B. (2013). The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model. Wilmott Magazine (англ.). 2013 (67): 50—61. doi:10.1002/wilm.10252.
- ↑ Székely, G. J. Rizzo; Bakirov, N. K. (2007). Measuring and testing independence by correlation of distances. Annals of Statistics[en] (англ.). 35 (6): 2769—2794. arXiv:0803.4101. doi:10.1214/009053607000000505.
- ↑ Székely, G. J.; Rizzo, M. L. (2009). Brownian distance covariance. Annals of Applied Statistics (англ.). 3 (4): 1233—1303. arXiv:1010.0297. doi:10.1214/09-AOAS312. PMC 2889501. PMID 20574547.
- ↑ Lopez-Paz D. and Hennig P. and Schölkopf B. (2013). "The Randomized Dependence Coefficient", "Conference on Neural Information Processing Systems[en]" Reprint [Архівовано 3 серпня 2020 у Wayback Machine.] (англ.)
- ↑ Thorndike, Robert Ladd (1947). Research problems and techniques (Report No. 3) (англ.). Washington DC: US Govt. print. off.
- ↑ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). Scaled correlation analysis: a better way to compute a cross-correlogram. European Journal of Neuroscience (англ.). 35 (5): 1—21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876.
- ↑ Higham, Nicholas J. (2002). Computing the nearest correlation matrix—a problem from finance. IMA Journal of Numerical Analysis (англ.). 22 (3): 329—343. CiteSeerX 10.1.1.661.2180. doi:10.1093/imanum/22.3.329.
- ↑ Portfolio Optimizer. portfoliooptimizer.io (англ.). Архів оригіналу за 3 січня 2022. Процитовано 30 січня 2021.
- ↑ Borsdorf, Rudiger; Higham, Nicholas J.; Raydan, Marcos (2010). Computing a Nearest Correlation Matrix with Factor Structure (PDF). SIAM J. Matrix Anal. Appl. (англ.). 31 (5): 2603—2622. doi:10.1137/090776718. Архів оригіналу (PDF) за 30 грудня 2021. Процитовано 3 січня 2022.
- ↑ Qi, HOUDUO; Sun, DEFENG (2006). A quadratically convergent Newton method for computing the nearest correlation matrix. SIAM J. Matrix Anal. Appl. (англ.). 28 (2): 360—385. doi:10.1137/050624509.
- ↑ Park, Kun Il (2018). Fundamentals of Probability and Stochastic Processes with Applications to Communications (англ.). Springer. ISBN 978-3-319-68074-3.
- ↑ Aldrich, John (1995). Correlations Genuine and Spurious in Pearson and Yule. Statistical Science (англ.). 10 (4): 364—376. doi:10.1214/ss/1177009870. JSTOR 2246135.
- ↑ Mahdavi Damghani, Babak (2012). The Misleading Value of Measured Correlation. Wilmott Magazine[en] (англ.). 2012 (1): 64—73. doi:10.1002/wilm.10167.
- ↑ Anscombe, Francis J. (1973). Graphs in statistical analysis. The American Statistician (англ.). 27 (1): 17—21. doi:10.2307/2682899. JSTOR 2682899.
- ↑ Taraldsen, Gunnar (2021). The confidence density for correlation. Sankhya A (англ.). 85: 600—616. doi:10.1007/s13171-021-00267-y. ISSN 0976-8378. S2CID 244594067.
- ↑ Taraldsen, Gunnar (2020). Confidence in correlation. researchgate.net (preprint) (англ.). doi:10.13140/RG.2.2.23673.49769.
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Гнеденко Б. В. Курс теории вероятностей. — 6-е изд. — Москва : Наука, 1988. — 446 с.(рос.)
- Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
- Cohen, J.; Cohen P.; West, S.G. & Aiken, L.S. (2002). Applied multiple regression/correlation analysis for the behavioral sciences (англ.) (вид. 3rd). Psychology Press. ISBN 978-0-8058-2223-6.
- Hazewinkel, Michiel, ред. (2001), Correlation (in statistics), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4 (англ.)
- Oestreicher, J. & D. R. (26 лютого 2015). Plague of Equals: A science thriller of international disease, politics and drug discovery (англ.). California: Omega Cat Press. с. 408. ISBN 978-0963175540.
| У Вікісловнику є сторінка кореляція. |
| Вікісховище має мультимедійні дані за темою: Кореляція |
- Сторінка MathWorld про коефіцієнт/и (взаємної) кореляції вибірки [Архівовано 31 серпня 2019 у Wayback Machine.] (англ.)
- Обчислення значущості між двома кореляціями [Архівовано 3 січня 2022 у Wayback Machine.] для порівняння двох значень кореляції.
- Інструментарій MATLAB для обчислювання коефіцієнтів зваженої кореляції. Архів оригіналу за 24 квітня 2021.
- Доведення того, що вибіркова двовимірна кореляція має межі плюс та мінус 1 [Архівовано 17 жовтня 2016 у Wayback Machine.] (англ.)
- Інтерактивна Flash-симуляція кореляції двох нормально розподілених змінних [Архівовано 17 травня 2021 у Wayback Machine.] від Юги Пуранена.
- Кореляційний аналіз. Біомедична статистика (англ.)
- R-Psychologist Correlation [Архівовано 17 серпня 2020 у Wayback Machine.]: унаочнення кореляції між двома числовими змінними
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|









![{\displaystyle \rho _{X,Y}=\operatorname {corr} (X,Y)={\operatorname {cov} (X,Y) \over \sigma _{X}\sigma _{Y}}={\operatorname {E} [(X-\mu _{X})(Y-\mu _{Y})] \over \sigma _{X}\sigma _{Y}},\quad {\text{if}}\ \sigma _{X}\sigma _{Y}>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b551ad29592ae746bf05fe397fbdc56201f483a5)
















![{\displaystyle {\begin{aligned}r_{xy}&={\frac {\sum x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{ns'_{x}s'_{y}}}\\[5pt]&={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-(\sum x_{i})^{2}}}~{\sqrt {n\sum y_{i}^{2}-(\sum y_{i})^{2}}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6da33b8144a5e67959969ef2c4830ece1938bbb2)











![{\displaystyle {\begin{aligned}\rho _{X,Y}&={\frac {1}{\sigma _{X}\sigma _{Y}}}\mathrm {E} [(X-\mu _{X})(Y-\mu _{Y})]\\[5pt]&={\frac {1}{\sigma _{X}\sigma _{Y}}}\sum _{x,y}{(x-\mu _{X})(y-\mu _{Y})\mathrm {P} (X=x,Y=y)}\\[5pt]&=\left(1-{\frac {2}{3}}\right)(-1-0){\frac {1}{3}}+\left(0-{\frac {2}{3}}\right)(0-0){\frac {1}{3}}+\left(1-{\frac {2}{3}}\right)(1-0){\frac {1}{3}}=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75bf2b7806338758b4c55d7b4f18a5071b8e919b)

![{\displaystyle [0,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f32245981f739c86ea8f68ce89b1ad6807428d35)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)





























